Ondes,
interférences, diffraction. Concours audioprothésiste Bordeaux 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Un
faisceau laser se propageant dans l'air arrive à l'interface air
/ verre avec un angle d'incidence de 13°. Quel est l'angle de
réfraction ? ( 19,5° ; 8,6 ° ;
40,5 ° ; 0,3 ° ; 8,7 ° ).
nair
sin i = nverre sin r ; sin i = 1,5 sin r ; sin r = sin
13 / 1,5 = 0,150 ; r = 8,6 °.
Donnez l'angle de réflexion totale à l'interface eau/ air. (48,8 ° ; 41,2 ° ; 46,2 ;
50,3 ° ; 37,9 °)
sin ilim
= nair/ neau = 1/,33 = 0,752 ; ilim
= 48,8 °.
Quelle est la longueur d'onde dans l'air du signal sonore dont
l'oscillogramme est représenté ci-dessous ?
( 40 cm ; 0,85 mm ; 400 cm ; 21,25 cm ; 85 cm ).
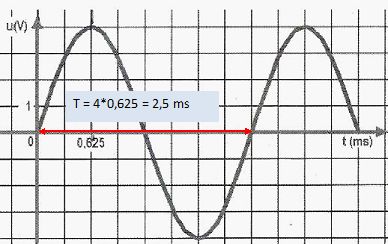
l = vson T = 340*2,5 10-3=0,85
m = 85 cm.
Si
un chanteur seul est perçu avec un niveau sonore de 65 dB, quel serait
le niveau sonore perçu dans le cas de trois chanteurs de même puissance
? ( 73 dB ; 71 dB ;
195 dB ; 70 dB ;
68 dB )
Pour un chanteur seul L = 10 log (I / I0)
;
pour trois
personnes chantant de manière identique : L' = 10
log (3I / I0) = L + 10 log 3 = 65+4,8=69,8 ~70 dB.
Si
25 violons jouant à la même puissance produisent un niveau sonore de 86
dB, quel est le niveau sonore d'un seul violon ?
(61 dB ; 72 dB ;
62 dB ; 3 dB ; 75 dB ).
L =86= 10 log ( 25 I / I0)
=10 log 25 +10 log (I / I0) ; 10 log (I
/ I0) =86-10 log 25 =72 dB.
La plage de fréquences sonores
audibles est en moyenne :
0 Hz - 20 MHz ; 20 Hz -
20 kHz (exact ) ; 20 Hz - 20 MHz ; 0 Hz - 20 kHz ; 0 Hz - 20 GHz.
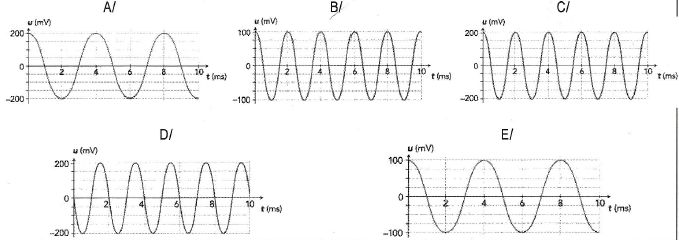
Quelle courbe correspond à l'équation suivante : u(t) = 200 cos (
2pt/(4 10-3)) ?
T = 4 10-3
s = 4 ms ; amplitude 200 mV.
Courbe A.
Un diapason émet un son pur ( sans
harmonique ) de fréquence 880 Hz. Au bout de quelle durée ce son est-il
perçu par une personne située à 10 m du diapason ? (88 s ; 88 ms ; 29 ms ; 11 ms ; 64 ms ).
t = d / vson
= 10 / 340 = 0,0294 s ~29 ms.
Un
diapason émet un son pur ( sans harmonique ) de fréquence 440 Hz.
L'intensité sonore perçue par une personne située à 10 m du diapason
est 12 10-10 W m-2. Quel est le niveau
d'intensité sonore correspondant ? ( 30 dB ; 31 dB ; 32 dB ; 33 dB ;
34 dB ).
L = 10 log (I / I0)
= 10 log ( 12 10-10 / 10-12)
=30,8 ~31 dB.
La figure ci-dessous, obtenu sur un écran disposée après deux fentes
éclairées par un laser, met en évidence deux phénomènes physiques.

Réfraction et réflexion ; diffraction et interférences ; diffraction et interférences ( exact ) ;
diffraction et réfraction ; interférences et diffusion.
La figure ci-dessous est obtenue en éclairant une fente par un laser de
longueur d'onde 632 nm. Cette figure est visualisée sur un écran situé
à D=70 cm de cette fente. Déterminer la largeur de cette fente. ( 26 µm ; 52 µm ; 0,9 µm ; 13 µm ;
34 µm ).
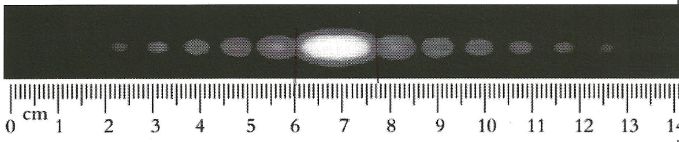
Largeur de la tache centrale de
diffraction L ~1,7 cm ;
L = 2lD / a soit a = 2lD/L = 2*0,632 *70 / 1,7 ~ 52 µm.
|
|
|
Une fente de largeur "a" est éclairée par un
faisceau laser. Pour différentes largeurs de fente, on a mesuré la
demi-largeur angulaire q de
la tache centrale de la figure obtenue sur un écran. Les résultats ont
permis de tracer le graphe ci-dessous sur lequel une interpolation
linéaire a été effectuée. Déduisez-en la longueur d'onde du laser.
( 1040 nm ; 260 nm ; 15,6 µm ; 156 nm ; 520 nm ).
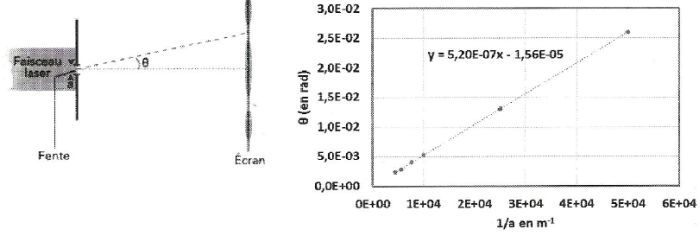
q = l/a ; le coefficient directeur de la droite
est égal à la longueur d'onde soit 0,52 µm = 520 nm.
Même question. ( 543 nm ; 531 nm ; 552 nm ; 576 nm ; 512 nm
).
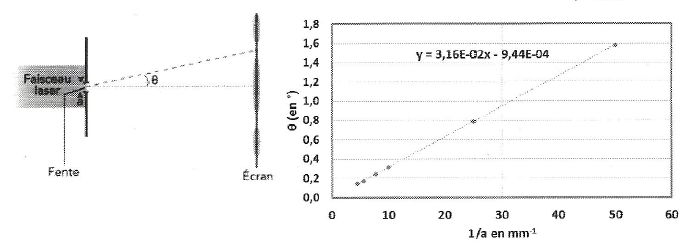
Le coefficient
directeur de la droite est égal à la longueur d'onde soit 3,16 10-2
mm = 3,16 10-5 m
q = l /a ; q en rad et a en m ; q *3,14/180= l /(a 10-3) ; q en degré et a en mm.
q = 180 103
/ 3,14 l / a = 5,73 104
l/a ; 5,73 104
l = 3,16 10-2
; l = 5,5152 10-7 m = 552 nm.
Même question. ( 702 nm ; 583 nm ; 632 nm ; 646 nm ; 904 nm ).
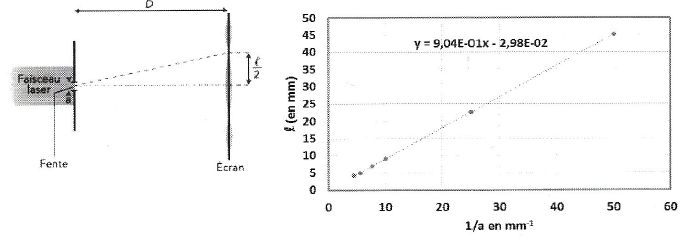
l = 2lD / a avec l, l, D et a en mètre ; 10-3l =
2lD / (a 10-3) avec l, D en mètre et l et a en mm.
l = 2lD 106 / a ; 2lD 106 =0,904 ; l =0,90410-6 /(2*0,70)
= 6,46 10-7 m = 646 nm.
|
|
|
Le phénomène qui permet de mettre en évidence le
caractère ondulatoire de la lumière est : la réflexion ; la propagation
; la diffraction (
exact ) ; la réfraction ; l'atténuation.
Pour observer une figure d'interférences en lumière monochromatique, il
faut :
deux lampes monochromatiques identiques
indépendantes ;
deux lampes monochromatiques identiques
branchées sur le même générateur ;
une seule
lampe monochromatique munie d'un système permettant d'obtenir deux
sources secondaires ( exact ) ;
deux lampes quelconques ;
deux lampes quelconques branchées sur le même générateur.
Une onde sonore se propageant dans l'air :
est
longitudinale ( exact ) ;
est de même nature que la lumière ;
est de même nature que les ondes radio ; est transversale ; possède une
vitesse de 340 km/h.
Une onde est dite progressive :
si son amplitude augmente avec le temps ;
si elle se
propage dans une direction de l'espace ; (exact )
si elle est immobile dans l'espace ; si elle possède une fréquence
unique ; si elle est longitudinale.
Deux ondes qui se croisent :
sont obligatoirement modifiées après leur rencontre ; s'arrêtent : il
n'y a plus d'onde ;
peuvent
poursuivre inchangées après leur rencontre ( exact ) ; changent
de fréquence ; poursuivent leur chemin mais atténuées.
On réalise des interférences avec des fentes d'Young, les deux fentes
de largeur a étant très proches l'une de l'autre, espacées d'une
distance b. Sur l'écran, les franges d'interférences sont visibles en
particulier dans la tache de diffraction. On compte 11 franges
brillantes dans cette tache centrale de diffraction. Calculer le
rapport b/a. (11 ; 5,5
; 1 ; 22 ; 44 ).

On compte 10
interfranges i avec i = lD/ b.
Largeur de la tache
centrale de diffraction : L = 2 l
D/a= 10 i = 10 lD/b ;
1 / a = 5 / b ; b/a = 5.
Dans le cas de la diffraction d'une onde lumineuse monochromatique de
longueur d'onde l par une
fente de largeur "a", la tache centrale de diffraction a pour largeur
angulaire :
l/a ; 2 l/a ( exact ) ; a/l ; 2a/l ; (l/a)2.
Par rapport au son, la lumière se propage :
102 fois plus vite ; 104 fois plus vite ; 106 fois plus vite ; 108 fois plus vite ; 1010 fois plus vite.
Dans l'air : 3 108
/ 340 ~106.
Parmi les milieux matériels suivants, celui dans lequel la célérité du
son est la plus grande est :
aluminium
( exact) ; huile ; eau ; air ; hélium.
Un son émis par un haut-parleur est une onde :
mécanique,
longitudinale, progressive ( exact) ;
mécanique, transversale, stationnaire ;
électromagnétique, transversale, progressive ;
électromagnétique, longitudinale, stationnaire ; mécanique,
électromagnétique, progressive.
La lumière qui nous vient du soleil est une onde :
mécanique longitudinale progressive ; mécanique, transversale, stationnaire ; électromagnétique,
transversale, progressive (exact ) ;
électromagnétique, longitudinale, stationnaire ;
mécanique, électromagnétique, progressive.
La célérité d'une onde mécanique qui parcourt une distance de 800 m en
une durée Dt = 4,0 s est
: 50 m/s ; 200 km/s ; 720 km/h ; 3200 m/s ; 5
mm/s.
800/4,0 = 200 m/s ou
200*3,6 = 720 km/h.
|
|
|
Dans
une piscine, un haut-parleur accroché au mur émet dans l'air une onde
musicale de fréquence f0 = 338 Hz. La fréquence perçue dans l'eau par
le plongeur est :
276 Hz ; 338 Hz ; 1491 Hz ; il ne peut pas entendre le son,
qui n'a pas été émis dans l'eau ( exact) ; 77 Hz.
Seulement 0,1 % de la puissance sonore est
transmise à la traversée du dioptre eau-air.
Une onde luminneuse de longueur d'onde dans le vide 492 nm, se propage
dans du verre. Cette lumière est de couleur :
ultraviolette ; bleue
( exact ); orange ; infrarouge ; magenta.
Une
onde luminneuse de longueur d'onde dans le vide 492 nm, se propage dans
du verre. Sa longueur d'onde dans le milieu considéré est : 492 nm ; 328 nm ; 738 nm ; 503 nm
; 632 nm.
lverre = l0
/ nverre = 492/1,5 =328 nm.
La relation liant la fréquence f ou la période T à la longueur d'onde l ( en notant v la célérité ) est
: v = lf ( exact ); f = l/v ; l = v f ; l = v /T ; f = lT.
Sur l'écran d'un oscilloscope on visualise les variations de la tension
électrique aux bornes d'un microphone, au cours du temps. Les calibres
sont : 5 mV / div et 0,5 ms / div.
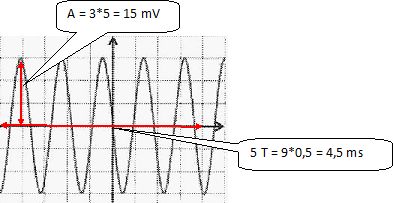
La période temporelle est : 0,3 ms ; 0,9 ms ( exact ) ; 1,1
ms ; 1,5 ms ; 0,6 ms.
L'amplitude de la tension est :0,6 mV ;1,5 mV ; 3 mV ; 15 mV ( exact ) ; 30 mV.
La valeur efficace de la tension est :10,6 mV ; 15 mV ; 1,5 mV
; 21,2 mV ; 30 mV.
15/1,414 ~ 10,6 mV.
Le son d'une clarinette est enregistré par un microphone. Cette tension
est numérisée par un CAN 16 bits. La fréquence d'échantillonnage est
réglée à 48 kHz. Le débit binaire ( en kilobits par seconde ) du flux
audio associé à cet enregistrement est : 262 kbps ; 768kbps ; 12 300
kbps ; 49 200 kbps ; 48 kbps.
16*48 = 768 kbps.
|
|
|







