Le grand 8.
Concours itpe 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
On
étudie le mouvement d'un wagonnet de grand 8. Les forces de frottement
sur les rails et la résistance de l'air sont négligées. On assimile le
véhicule à un point matériel. La vitesse initiale est nulle.
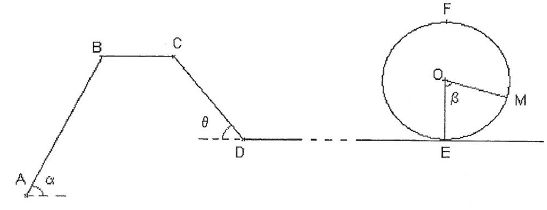
Il est tracté par un câble sur la piste AB de pente 55° et de longueur d = 20,0 m.
En appliquant le théorème de l'énergie cinétique, trouver la relation entre m, vB, g, d, a et la tension T du câble.
Le wagonnet est soumis à son poids, à l'action normale du plan et à la tension du câble.
Travail résistant du poids en montée : -mgd sin a.
Travail de la tension du câble : T d.
Le travail de l'action normale du plan est nul, force perpendiculaire à la vitesse.
Variation de l'énergie cinétique entre A et B : ½mvB2-0 =Td- mgd sin a.
T = m(0,5vB2/d+g sin a).
A.N : vB = 2 m/s ; m =600 kg.
T = 600(0,5*4 / 20 +9,81 sin 55) =4,88 103 N.
Après une partie horizontale BC, le wagonnet aborde une pente descendante CD de longueur L = 10 m à la vitesse vC. q = 40,0°.
Quelle est la vitesse vC ? Justifier sans calcul.
Sur
la partie horizontale, le wagonnet est soumis à son poids et à l'action
normale du plan. Ces force perpendiculaires à la vitesse ne travaillent
pas. L'énergie cinétique, et en conséquence la vitesse, restent
constantes.
Quelle est la vitesse vD ?
Travail moteur du poids ( descente ) entre C et D : mgL.
le travail de l'action normale du plan est nul.
Th de l'énergie cinétique entre C et D : ½mv2D-½mv2C = mg Lsin q.
v2D =v2C +2 g Lsin q ; vD = (v2C +2 g Lsin q)½=(4+2*9,81*10*sin 40)½=11,4 m/s.
Quelle devrait être la longueur du tronçon CD pour que vD = 4 m/s ?
v2D =v2C +2 g Lsin q ; L =(v2D -v2C ) / (2gsin q) = (16-4) /12,61=0,95 m.
|
| .
. |
|
|
Le
wagonnet aborde plus loin un looping de rayon R = 2,5 m. Soit ß l'angle
compris entre le vecteur OE et OM avec O centre du looping.
Justifier la conservation de l'énergie mécanique EM du wagonnet.
Sur le looping seul le poids travaille. Le poids est une force conservative.
On prend le point E comme origine de l'énergie potentielle de pesanteur.
|
.
|
|
Quelle doit être la vitesse minimum en E pour que le wagonnet puisse passer le looping ?
La liaison chariot-rails étant parfaite, l'action des rails sur le
charriot est perpendiculaire au rail. Les rails guident le chariot et
exerce une action dirigée vers O.
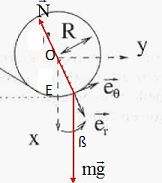
Expression de N en fonction de ß :
La seconde loi de Newton s'écrit suivant er : -N + mg cos ß = -mv2/R. (1)
Théorème de l'énergie cinétique entre E et la position repérée par ß :
½mv2 - ½mvE2 = -mgR(1-cos ß) ; v2 = v2E -2gR(1-cos ß) . Repport dans (1)
N = mg cos ß +m(v2E -2gR(1-cos ß))/ R = mg cos ß - 2mg( 1-cos ß)+mv2E/R
N = mg (3 cos ß-2) + mv2E/R
Le chariot doit rester au contact des rails : N >0 quelle que soit la valeur de ß, en particulier lorsque ß = p.
g (3 cos p-2) + v2E/R>0 ; -5g+v2E /R>0 ; vE>(5gR)½ ; vE > (5*9,81*2,5)½ ; vE >11,1 m/s.
|
|
Montrer que la vitesse v du wagonnet en M peut s'écrire : v = (v2E -2gR(1-cos ß))½.
Energie mécanique en E : ½mv2E.
Energie mécanique en M : ½mv2+mgR(1-cos ß).
Conservation de l'énergie mécanique : ½mv2E=½mv2+mgR(1-cos ß).
v2E=v2+2gR(1-cos ß) ; v2=v2E-2gR(1-cos ß).
A.N : ß =30° ; vE =11,1 m/s.
v = (11,12 -2*9,81*2,5(1-cos 30))½ =10,8 m/s
|
|
|