Etude
microscopique de l'aimantation, paramagnétisme, concours inspecteur
CCRF 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Étude
macroscopique de l’aimantation.
Rappels : Dans une région du vide où est appliqué une excitation
magnétique 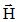 (au moyen d’une (au moyen d’une
bobine par exemple) règne un champ magnétique 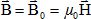 (B
exprimé en T, H en A/m). (B
exprimé en T, H en A/m).
Lorsque dans le champ 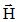 , est placé un matériau, ce
dernier est le siège d’une aimantation , est placé un matériau, ce
dernier est le siège d’une aimantation 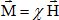 , ,
telle que le champ magnétique dans le matériau devient : 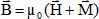
Comment
se nomme c ? Quelle est son
unité ?
La susceptibilité magnétique, faculté que possède un matériau à
s'aimanter sous l'action d'une excitation magnétique, est sans
dimension.
Dans le matériau, le champ magnétique s’écrit également 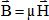 avec µ = µ0.µr et µr perméabilité relative du
matériau. Exprimer
µr en fonction de c.
avec µ = µ0.µr et µr perméabilité relative du
matériau. Exprimer
µr en fonction de c.
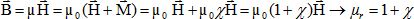
Étude
microscopique de l’aimantation : paramagnétisme.
Une explication du paramagnétisme a été apportée par Paul Langevin, en
considérant que les atomes de certains corps possédaient des moments magnétiques de spin
non nuls et indépendants les uns des autres. Ces moments magnétiques atomiques 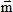 sont liés au
moment cinétique de spin d’un ou plusieurs électrons non appariés de l’atome (rotation de
l’électron sur lui-même), le moment orbital (lié à la rotation de l’électron autour de l’atome) étant nul. sont liés au
moment cinétique de spin d’un ou plusieurs électrons non appariés de l’atome (rotation de
l’électron sur lui-même), le moment orbital (lié à la rotation de l’électron autour de l’atome) étant nul.
On considère un milieu constitué d’atomes dans lesquels seul un
électron non apparié existe.
Le moment magnétique de spin de l’électron a pour intensité le magnéton
de Bohr µB.
Exprimer 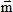 en fonction de µB. en fonction de µB.
Le milieu considéré est constitué d'atomes dont le moment cinétique se
réduit à un spin simple S = ½ sans moment cinétique orbital. Chaque atome possède un moment magnétique : 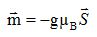 g : facteur de Landé égal à 2 pour l'électron. g : facteur de Landé égal à 2 pour l'électron.
Le milieu est placé dans un champ magnétique uniforme 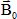 . On rappelle que l’énergie d’interaction entre un moment magnétique . On rappelle que l’énergie d’interaction entre un moment magnétique 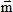 et un champ magnétique et un champ magnétique 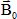 est donnée par est donnée par 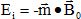 . .
Exprimer l’énergie d’interaction magnétique Ei d’un atome dont le moment 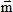 fait un angle q avec le champ fait un angle q avec le champ 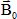 en fonction de µB, B0 et q. en fonction de µB, B0 et q.
Ei = -m B0 cosq = - µB B0 cos q .
|
| .
. |
|
|
Pour
simplifier les calculs, on considèrera par la suite que la distribution
des moments magnétiques atomiques dans l’espace se réduit à 2 positions
par rapport à 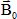 : parallèle et antiparallèle. : parallèle et antiparallèle.
Exprimer les 2 énergies d’interaction correspondantes.
q=0 : E1 = - µB B0.
q=180° : E2 = + µB B0.
|
.
|