Le cobalt et ses ions, théorie du champ cristallin, approximation de
Slater, concours inspecteur
CCRF 2012
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Configuration électronique du cobalt et ses ions.
Le Cobalt (Z = 27) peut donner les ions Cobalt II et III en perdant deux ou trois électrons de valence.
Donner la configuration électronique de l'atome de cobalt dans son état fondamental.
Atome : 1s2 2s2 2p6 3s2 3p6 4s2 3d7.
Donner les trois configurations électroniques envisageables pour l'ion cobalt II selon qu'il perd :
a) deux électrons s. 1s2 2s2 2p6 3s2 3p6 3d7.
b) 1 électron s et 1 électron d. 1s2 2s2 2p6 3s2 3p6 4s1 3d6.
c) 2 électrons d. 1s2 2s2 2p6 3s2 3p6 4s2 3d5.
Comparer les énergies orbitalaires de l'ion cobalt II pour chaque configuration électronique précédemment envisagée
en présentant le résultat sous la forme : E (Co II) = E (e- de coeur) +
E (e- externes). Le calcul orbitalaire des électrons de coeur E (e- de
coeur) n'est pas demandé. En déduire la configuration électronique la plus stable pour l'ion Cobalt II.

a) Configuration. 1s2 2s2 2p6 3s2 3p6 3d7.
Constante d'écran des autres électrons vis à vis d'un électron 3d : s3d =6*0,35+8*1 + 10*1 = 20,1.
Charge nucléaire effective : Z*=27-20,1 =6,9.
Energie d'un l'électron 3d :-(Z */n *) 2=-(6,9/3) 2=-5,29 Ry ou -13,6*5,29 =-71,94 eV.
Energie des 7 électrons 3d :-7*71,94 = -503,6 eV.
Energie électronique E = E(coeur)-503,6 eV.b) Configuration. 1s2 2s2 2p6 3s2 3p6 4s1 3d6.
Constante d'écran des autres électrons vis à vis d'un électron 4s : s4s =14*0,85 + 10*1 = 21,9.
Charge nucléaire effective : Z*=27-21,9 =5,1.
Energie d'un l'électron 4s :-(Z*/n*)2=-(5,1/3,7)2=-1,9 Ry ou -13,6*1,9 =-25,8 eV.
Constante d'écran des autres électrons vis à vis d'un électron 3d : s3d =5*0,35+8*1 + 10*1 = 19,75.
Charge nucléaire effective : Z*=27-19,75 =7,25.
Energie d'un l'électron 3d :-(Z*/n*)2=-(7,25/3)2=-5,84 Ry ou -13,6*5,84 =-79,4 eV.
Energie électronique E = E(coeur)-25,8-6*79,4=E(coeur)-502,4 eV.c) Configuration : 1s2 2s2 2p6 3s2 3p6 4s2 3d5.
Constante d'écran des autres électrons vis à vis d'un électron 4s : s4s =0,35+13*0,85+10*1 = 21,4.
Charge nucléaire effective : Z*=27-21,4 =5,6.
Energie d'un l'électron 4s :-(Z*/n*)2=-(5,6/3,7)2=-2,292 Ry ou -13,6*2,29= -31,15 eV.
Constante d'écran des autres électrons vis à vis d'un électron 3d : s3d =4*0,35+8*1 + 10*1 = 19,4.
Charge nucléaire effective : Z*=27-19,4 =7,6.
Energie d'un l'électron 3d :-(Z*/n*)2=-(7,6/3)2=-6,425 Ry ou -13,6*6,42 =-87,3eV
Energie électronique E = E(coeur)-2*31,15-5*87,3=E(coeur)-499 eV.
La configuration 1s2 2s2 2p6 3s2 3p6 3d7 est la plus stable : elle correspond à l'énergie électronique la plus basse.
|
| .
. |
|
|
Théorie du champ cristallin pour les ions du cobalt.
Les ions cobalt II et cobalt III donnent en présence de ligands des ions complexes de structure octaédrique.
Selon cette théorie, quelle est la nature de la liaison entre l'élément central et ses coordinats ?
Liaison covalente de coordination.
Expliquer pourquoi dans un complexe octaédrique, les orbitales d sont séparées en deux groupes d'énergies différentes.
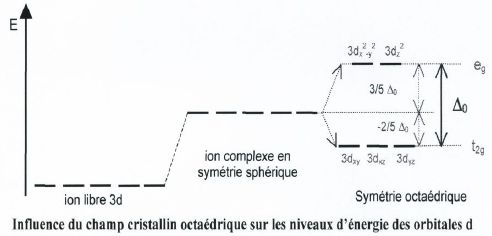
Les 5 O.A nd d'un élément chimique ont la même énergie :
elles sont dégénérées. Lorsqu'un élément de transition subit l'influence du
champ électrostatique de ligands il y a levée partielle de dégénérescence. Dans
le cas du champ octaèdrique les O.A se séparent en deux niveaux :
niveau t2g : les orbitales dxy,
dyz et dxz qui ne pointent pas en direction des ligands
sont stabilisées.
niveau eg : les orbitales dx²-y² et
dz² pointent en direction des ligands et sont
déstabilisées. Il y a éclatement des niveaux énergtiques en deux sous niveaux : D0 représente l'énergie d'éclatement du champ cristallin.
Représenter un diagramme traduisant la levée partielle de dégénérescence des OA d en orbitales eg et en orbitales t2g.
|
.
|
|
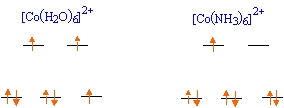
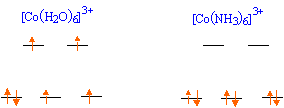
On considère les ions suivants : a) [Co(H2O)6]2+ ; b) [Co(H2O)6]3+ ; c) [Co(NH3)6]2+ ; d) [Co(NH3)6]3+.
Nommer ces ions.
ion hexaaquocobalt (II) ; ion hexaaquocobalt (III) ; ion hexaaminocobalt (II) ; ion hexaaminocobalt (III).
En
considérant, dans le cas des ions Cobalt II et III, l'eau comme un
ligand à champ faible et l'ammoniac comme un ligand à champ fort, représenter le remplissage des niveaux électroniques 3d de ces ions.
Un ligand à champ fort
est un ligand pour lequel l'éclatement
D0
du champ cristallin est supérieur à
l'énergie d'appariement P : le maximum d'électrons sont
appariés et le spin est faible.
Un ligand à champ faible est
un ligand pour lequel l'éclatement
D0
du champ cristallin est inférieur à
l'énergie d'appariement P : le maximum d'électrons sont
célibataires et le spin est fort.
Une substance paramagnétique
possède au moins un électron
célibataire.
|
|
|
paramagnétique .....
paramagnétique
|
paramagnétique........diamagnétique
|
| µB =3,9 µB =1,7 | µB =4,9 µB=0 |
Calculer le nombre effectif du magnéton de Bohr de chaque ion complexe.
Le magnéton de Bohr µB caractérise le nombre n d'électrons célibataires dans une
sous-couche 3d : µB = (n(n+2))½.
Justifier le caractère plus réducteur de l'ion [Co(NH3)6]2+ par rapport à l'ion [Co(H2O)6]2+
Un e espèce est dautant plus réductrice qu'elle cède plus facilement un électron : la perte d'un électron par [Co(NH3)6]2+conduit à un niveau t2g saturé.
Calculer l'énergie de stabilisation du champ cristallin (ESCC) en symétrie
octaédrique pour les ions [Co(H2O)6]3+ et [Co(NH3)6]3+.
données :
D0
énergie d'éclatement du champ cristallin
; P énergie moyenne d'appariement de 2
électrons.
|
[Co(H2O)6]3+
|
[Co(NH3)6]3+
|
|
D0
kJ/mol
|
218
|
274
|
|
P kJ/mol
|
226
|
226
|
Pour
[Co(H2O)6]3+ on
observe deux électrons sur le niveau eg et
quatre électrons sur le niveau t2g
:
ESCC = Eeg - E
t2g = [2 * (3/5 D0)
- 4 *(2/5 D0)]
= -2/5D0
= -87,2
kJ/mol.
Pour
[Co(NH3)6]3+ on
observe aucun électrons sur le niveau eg
et six électrons sur le niveau t2g
:
ESCC = Eeg - E
t2g = [ 0 * (3/5 D0)
- 6 *(2/5 D0)]
= -12/5D0
= -657,6
kJ/mol.
Configuration électronique du Calcium.
Donner la structure électronique du calcium Ca, Ca+, Ca2+ et Ca3+.
Ca : 1s2 2s2 2p6 3s2 3p6 4s2 ; Ca+ : 1s2 2s2 2p6 3s2 3p6 4s1 ; Ca2+ : 1s2 2s2 2p6 3s2 3p6 ; Ca3+ : 1s2 2s2 2p6 3s2 3p5.
Calculer,
en utilisant les facteurs d'écran de Slater, l'énergie de première, de
seconde et de troisième ionisation du calcium (I1, I2, I3) ainsi que les longueurs d'onde minimales des photons (l1, l2, l3) qui vont permettre ces ionisations. Dans quel domaine du spectre se situent-elles ?
Ca : 1s2 2s2 2p6 3s2 3p6 4s2 ;
Constante d'écran des autres électrons vis à vis d'un électron 4s : s4s =0,35+8*0,85+10*1 = 17,15.
Charge nucléaire effective : Z*=20-17,15 =2,85.
Energie d'un l'électron 4s :-(Z*/n*)2=-(2,85/3,7)2=-0,593 Ry ou -13,6*0,593= -8,0695 eV ou -8,069*1,6 10-19 =-1,29 10-18 J.
Ca+ : 1s2 2s2 2p6 3s2 3p6 4s1 ;
Constante d'écran des autres électrons vis à vis d'un électron 4s : s4s =8*0,85+10*1 = 16,8.
Charge nucléaire effective : Z*=20-16,8 =3,2.
Energie d'un l'électron 4s :-(Z*/n*)2=-(3,2/3,7)2=-0,748 Ry ou -13,6*0,748= -10,17 eV ou -10,17*1,6 10-19 =-1,63 10-18 J.
Energie de première ionisation : I1= -1,63 10-18 -2(1,29 10-18 )=9,5 10-19 J ; l1=hc/I1 =6,67 10-34*3 108 / (9,5 10-19) =2,1 10-7 m = 0,21 µm ( domaine UV).
Ca2+ : 1s2 2s2 2p6 3s2 3p6 ; il n'y a plus d'électron 4s ; l'énergie
orbitalaire de l'électron 4s est connue.
D'où l'énergie de seconde ionisation du calcium : I2 = 1,63 10-18 J.
l2=hc/I2 =6,67 10-34*3 108 / (1,63 10-18) =1,23 10-7 m = 0,123 µm ( domaine UV).
Ca2+ : 1s2 2s2 2p6 3s2 3p6 ;
Constante d'écran des autres électrons vis à vis d'un électron 3p : s3p =7*0,35+8*0,85+2 = 11,25.
Charge nucléaire effective : Z*=20-11,25 =8,75.
Energie d'un l'électron 4s :-(Z*/n*)2=-(8,75/3)2=-8,51 Ry ou -13,6*8,51= -115,69 eV ou -10,17*1,6 10-19 =-1,85 10-17 J.
Ca3+ : 1s2 2s2 2p6 3s2 3p5 ;
Constante d'écran des autres électrons vis à vis d'un électron 3p : s3p =6*0,35+8*0,85+2 = 10,9.
Charge nucléaire effective : Z*=20-10,9 =9,1.
Energie d'un l'électron 4s :-(Z*/n*)2=-(9,1/3)2=-9,2 Ry ou -13,6*9,2= -125,35 eV ou -10,17*1,6 10-19 =-2,00 10-17 J.
Energie de troisième ionisation : I3= 6(-1,85 10-17 )-5(-2,00 10-17 )=7,5 10-18 J ; l1=hc/I1 =6,67 10-34*3 108 / (7,5 10-18) =2,67 10-8 m = 0,027 µm ( domaine UV).
En déduire la charge usuelle de cet élément. Justifier.
Ca2+ : la couche électronique externe est saturée.
|
Des propriétés du carbone.
Les deux variétés allotropiques les plus courants du carbone sont le carbone graphite et le carbone diamant. Expliquer le terme allotropique.
Certains corps simples existent sous des formes cristallines ou moléculaires différentes.
Pour l'une et l'autre des variétés allotropiques :
Décrire
les types de liaison. Décrire l'arrangement des atomes de carbone et
faire un schéma des structures géométriques élémentaires.
Diamant : structure critalline cubique à face centrée. Liaison covalente, hybridation de type sp3.
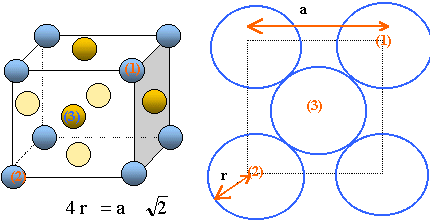
Le graphite est formé de couches hexagonales
coplanaires.
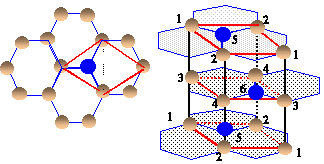
Dans le diamant la liaison C-C est simple alors que dans
le graphite ( hybridation de type sp2 ) elle est intermédiaire entre une liaison
simple et une liaison double.
Une de ces variétés a des propriétés isolantes alors que l'autre a des propriétés conductrices. Expliquer ces propriétés.
Grâce à la délocalisation des orbitales p, le graphite conduit l'électricité.
|
|
|