QCM photons, relativité restreinte, transfert thermique, CAN : concours
avenir 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Chaque bonne réponse est
gratifiée de 3 points, chaque mauvaise réponse est pénalisée d'un point.
On donne les premiers niveaux
énergétiques de l’atome de mercure :
E1 = –10,4 eV ; E2 = –5,5
eV ; E3 = –3,7 eV ; E4 =
–1,6 eV
Ici E1
représente l’énergie de liaison d’un électron de la couche périphérique
(la plus haute couche peuplée d’électrons) quand l’atome est dans son
état fondamental.
Que
se passe-t-il lors de l’absorption de lumière (un photon) par la
matière (un atome) ?
A)
l’atome est ionisé.
B)
il se produit une transition électronique vers un niveau supérieur.
C)
cela dépend de la couleur de la lumière.( Vrai ).
D)
un atome ne peut pas absorber un photon.
L’énergie échangée par l’atome pendant une transition électronique du
niveau 4 au niveau 2 est :
A)
-8,8 eV. B)
-3,9 eV.( Vrai ). C)
+3,9 eV. D)
+8,8 eV.
L'atome cède
de l'énergie au milieu extérieur sous forme de photon :
E2-E4 =-5,5 -(-1,6) =-3,9 eV.
La
relation qui permet de calculer la longueur d’onde l
du photon associé à cet échange d’énergie E est (avec c la célérité de
la lumière dans le vide et h la constante de Planck) :
A)
l =ch/E.( Vrai ) B) l = cE/h. C) l =E/(ch). D) l = h/(cE).
L’atome de mercure, à l’état
fondamental, entre en collision avec un électron possédant une énergie
cinétique Ec = 5,0 eV. Une valeur
possible de l’énergie cinétique de l’électron après collision est
:
A) 1,3 eV. B) 2,1 eV. C)
2,9 eV ( Vrai ) . D) 4,0 eV : l'électron
incident ne peut pas échanger d'énergie avec l'atome.
L'atome peut
absorber l'énergie : E2-E1 = -5,5 -(-10,4) = 4,9 eV.
L'électron possède après collision l'énergie cinétique 5-4,9 = 0,1 eV. L'atome peut absorber l'énergie
: E3-E2 = -3,7 -(-5,5) = 1,8 eV.
L'électron possède après collision l'énergie cinétique 5-1,8 = 3,2 eV.
L'atome peut absorber l'énergie
: E4-E2 = -1,6 -(-5,5) = 3,9 eV.
L'électron possède après collision l'énergie cinétique 5-3,9 = 1,1 eV.
L'atome peut absorber l'énergie
: E4-E3 = -16 -(-3,7) = 2,1 eV.
L'électron possède après collision l'énergie cinétique 5-2,1 = 2,9 eV.
|
| .
. |
|
|
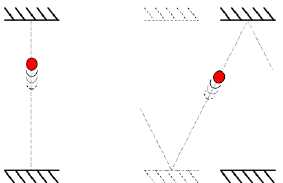
L’horloge
la plus simple, même si elle n’existe que par la pensée, est constituée
de deux miroirs parallèles en regard, entre lesquels va et vient un
photon à la célérité c (supposée égale à sa célérité dans le vide). Les
miroirs sont espacés de d = 15 cm, de sorte de l’on compte une durée
égale à une seconde, chaque fois que le photon parcourt un certain
nombre d’allers et retours d’un miroir à l’autre.
Le
nombre d’allers et retours entre les miroirs est :
A)
106. B)
107. C) 109.( Vrai ). D) cela dépend du
référentiel.
3 108 / (0,15+0,15) = 109.
Soit Dt
la durée du trajet du photon d’un miroir à l’autre quand les miroirs
sont immobiles (schéma de gauche : c’est la durée du trajet de longueur
d), et Dt’
cette même durée quand les miroirs sont en translation rectiligne vers
la droite à la vitesse v (schéma de droite). La
distance d’ parcourue par le photon d’un miroir à l’autre augmente donc
et vaut :
A) d'=(d2+v2Dt'2)½.( Vrai ).
B) d' =d/(1-v2/c2)½.
C) d'=d(1+vDt').
D) aucune de ces
réponses.
La durée
Dt’ est donc :
A)
Dt'
= Dt(1+v/c).
B)
Dt'
= Dt(1-v2/c2)-½.( Vrai ).
C)
Dt'
= Dt(1-v2/c2)+½.
D)
aucune de ces réponses.
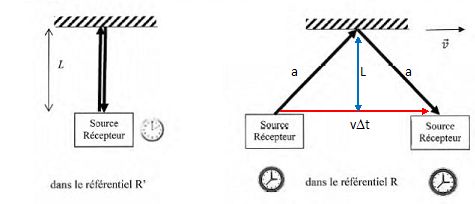
Dans le référentiel R' : Dt' = 2L/c. Dans
le référentiel R,
l'impulsion parcourt la distance 2a telle que : a2
= L2
+(½vDt)2.
Dt
=2a / c = 2 (L2
+(½vDt)2))½
/ c =2
((L/c)2 +(½ v/ c Dt)2))½.
Dt = 2((½Dt' )2
+(½ v/ c Dt)2))½
; Dt2
=Dt'
2
+ v2/ c2 Dt2 ;
Dt 2
(1-v2/ c2)=Dt' 2
; Dt
=Dt'
/(1-v2/
c2)½.
Ces
calculs montrent que :
A)
le temps s’écoule plus lentement dans le référentiel lié au sol.
B)
le temps s’écoule plus lentement dans le référentiel lié aux miroirs.( Vrai ).
C) le photon n’a pas
la même vitesse dans les deux cas.
D)
dans le référentiel lié aux miroirs, c’est le sol qui possède un
mouvement de translation : le problème devrait être symétrique, donc on
ne montre rien.
|
.
|
|
L’entrée
des rayons cosmiques dans la haute atmosphère génère une pluie de
particules, notamment des muons. Mais ces particules ne sont pas
stables : celles fabriquées en laboratoire se désintègrent en 10 μs
environ (au maximum) ; pourtant, on estime que les muons traversant
l’atmosphère à une vitesse proche de celle de la lumière, doivent «
vivre » au moins 0,1 ms, puisque nous les détectons au niveau du sol.
Leur vitesse minimale, par rapport à la célérité c de la lumière dans
le vide, est :
A) 0,9½c
. B) 0,99½c.
( Vrai ). C) 0,999½c. D) 0,9999½c.
0,1 ms = 100 µs
; 100 = 10 (1-v2/c2)-½ ; 10=(1-v2/c2)-½ ; 10(1-v2/c2)+½ =1 ; 100(1-v2/c2)
=1 ; 1-v2/c2=
0,01 ; v2/c2=0,99
; v/c =0,99½ .
L’unité de
la résistance thermique est :
A)
kelvin par watt. ( Vrai )
B) watt par kelvin
par mètre carré.
C)
watt par degré Celsius.
D)
kelvin par watt par mètre carré.
Un
des murs d’une maison a une superficie S. Comme il est en contact avec
le milieu extérieur, il est d’abord constitué d’une épaisseur e de
béton, de conductivité thermique l.
La
résistance thermique du mur est :
A) Sl/e. B) l/(Se). C) Se/l. D) e/(Sl). ( Vrai ).
L’isolation thermique
du mur est réalisée par un panneau en polystyrène extrudé d’épaisseur
e’, collé sur toute la surface du mur extérieur. La conductivité
thermique du polystyrène extrudé est l'.
La
résistance thermique totale de l’ensemble {mur+polystyrène} est
:
A) 1/S[e/l+e'/l'].( Vrai ). Les résistances thermiques
s'ajoutent.
B) S(ee'/(le'+l'e). C) S(l/e+l'/e'). D) T0=1/S[l l'/(le'+l'e)].
La différence de température entre l’intérieur de la maison et
l’extérieur est DT.
Le
flux thermique total F à travers
le mur et l’isolant est :
A)
DT/Rth
totale.( Vrai ). B)
Rth totaleS/DT. C) Rth totale/(SDT). D)
aucune de ces réponses.
On donne : DT = 20 °C, S = 20
m2, e = 50 cm, e’ = 6 mm, l = 2 W.°C.m–1,
l'
= 0,03 W.°C.m–1.
Le
flux thermique total est donc :
A)
0,02 W. B)
50 W. C)
900 W.( Vrai ). D) 3000 W.
Rth
totale =1/S[e/l+e'/l'] = 1/20 [0,50/2
+0,006/0,03]=0,05(0,25 +0,20) =0,05*0,45 =0,0225 K W-1.
F
= DT/Rth
totale=20/0,0225 ~
900 W.
|
Le son d’une clarinette,
enregistré par un microphone, est reproduit ci-dessous.
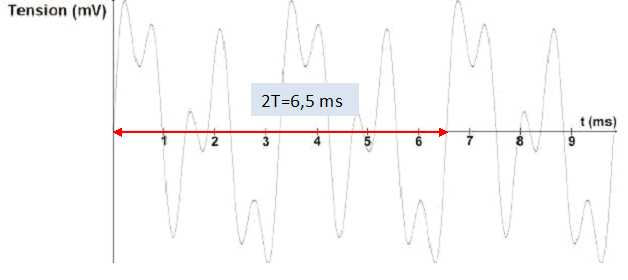
Cette tension est ensuite numérisée par un convertisseur
analogique-numérique 16 bits.
La
fréquence du signal analogique est de :
A) 306 Hz.( Vrai ). B) 916 Hz. C) 1412 Hz. D) 2468 Hz.
T = 3,25 10-3 s ; f = 1/T = 1/(3,25 10-3) =1000 / 3,25 ~306 Hz.
Parmi les
propositions suivantes et selon le théorème de Shannon, la
fréquence d’échantillonnage la plus basse permettant de restituer
correctement les harmoniques de ce son de clarinette est :
A) 700 Hz. B) 4 kHz.( Vrai ). C) 22 KHz. D) 44 kHz.
Après numérisation, les
valeurs possibles pour chaque échantillon vont de zéro à :
:
A) 255. B) 1023. C) 65535.( Vrai ). D) 1 048 575.
216-1
=65535.
La fréquence d’échantillonnage est
maintenant réglée à 48 kHz. Le débit
binaire du flux audio associé à cet enregistrement est :
A) 262 kbps (
kilobits par seconde). B)
768 kbps.( Vrai ). C) 12300 kbps. D) 49200 kbps.
48*16 = 768
kbps.
|
|