QCM champ électrique, onde sonore, numérisation, quantité de mouvement,
interférences : concours Advance 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Mouvement dans
un champ électrique.
Un proton pénètre, avec une vitesse v0 dans un champ
électrique uniforme E créé entre deux plaques métalliques reliées à un
générateur.
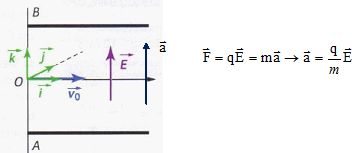
Données :
Charge du proton : q = 1,6.10-19 C ; masse du proton : m =
1,6 .10-27 kg ; E = 5,0.103 V.m-1.
A. La plaque
supérieure est reliée à la borne positive du générateur. Faux.
Le champ électrique
pointe vers le plus petit potentiel, la plaque reliée à la borne
négative du générateur.
B. La force
électrique F exercée sur le proton à la date t = 0 a pour intensité F =
8,0.10-16 N. Vrai.
F = qE = 1,6 10-19
*5 103 = 8,0 10-16
N.
C. Le vecteur
accélération de la particule est de direction verticale et orienté vers
le haut. Vrai.
D.
L’accélération est constante et vaut a = 5.1011 m.s-2.Vrai.
a
= 1,6 10-19 *5 103
/ (1,6 10-27)=5 1011
m s-2.
E. L’équation de la
trajectoire s’écrit : z = ½qE/(mv02) x2
+v0x. Faux
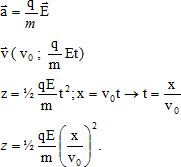
Onde
sonore.
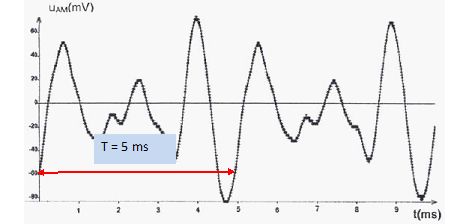
On enregistre la note jouée sur un violon à l’aide d’un microphone
relié à une interface d’acquisition. On obtient le
graphique ci-dessous.
Données :
vitesse du son dans l’air : V = 340 m.s-1 ; intensité sonore
de référence I0 = 10-12 W.m-2.
Aide au calcul : log x= n alors x = 10n.
A. Le signal est
périodique, il s’agit donc d’un son pur. Faux.
Le signal d'un son pur
est périodique sinusoïdal.
B. La longueur
d’onde, dans l’air, de l’onde sonore est λ= 1,7 m.Vrai.
l = vT = 340*5 10-3
=0,34*5 = 1,7 m.
Le spectre en fréquence obtenu à partir de cet enregistrement montre un
pic pour les cinq premiers harmoniques.
C. La fréquence du
troisième pic est 800 Hz. Faux.
Fréquence du fondamental f0 = 1/T = 1/(5 10-3) =
1000/5 = 200 Hz.
Première harmonique f1 = 400 Hz ; second harmonique f2
= 600 Hz ; trroisième harmonique : 4*200 = 800 Hz.
Le public reçoit un son de niveau sonore L =70 dB si un violoniste joue
seul.
D. Le violon émet
un son d’intensité sonore 10-5 W.m-2. Vrai.
I = I0 100,1 L
= 10-12 * 107 = 10-5 W.m-2.
Dans un orchestre, dix
violonistes jouent la même note avec le même niveau sonore que
précédemment.
Le son entendu par le public a un niveau
sonore de 80 dB. Vrai.
Intensité
sonore totale I = 10*0-5 = 10-4W.m-2.
Niveau sonore : 10 log (
10-4 / 10-12)
= 80 dB.
|
| .
. |
|
|
Numérisation.
Une image numérique est divisée en pixels disposés en ligne et en
colonne. Chaque pixel est composé de trois sous-pixels.
Chaque sous-pixel est codé par un octet utilisant le code binaire.
A. Le chiffre 3 en
code binaire s’écrit 011. Faux.
3 = 1* 20
+1*21 soit 11.
B. Il faut 24 bits
pour coder un pixel en RVB. Vrai.
Un octet ou 8 bits pour
chaque couleur primaire.
C.
Un pixel peut prendre 256 couleurs différentes. Faux.
256 teintes différentes
pour chaque couleur primaire.
D. Un pixel codé
R0V0B0 est blanc. Faux.
Aucune des couleurs
primaires n'est présentes : le pixel est donc noir.
E. Un pixel codé
R255V255B0 est jaune. Vrai.
Le
bleu est absent ; la superposition du rouge et du vert avec la même
intensité donne le jaune.
|
.
|
|
Quantité de
mouvement.
Une locomotive 1, de masse m1 = 3 t, avance sur un rail
horizontal et rectiligne à la vitesse V1 = 4 m.s-1
dans un référentiel terrestre. On assimilera les objets comme des
points matériels et indéformables. On néglige tout frottement.
A. La quantité de
mouvement de la locomotive dans un référentiel terrestre peut être
représenté par un vecteur parallèle aux rails et dirigé dans le sens du
mouvement. Vrai.
Les vecteurs quantité de
mouvement et vitesse sont proportionnels ; la constante de
proportionnalité est la masse, grandeur positive. Le vecteur vitesse a
toujours le sens du mouvement.
B. La quantité de
mouvement de la locomotive 1 dans le référentiel terrestre est p1
= 12 kg.m.s-1. Faux.
m1v1
= 3000*4 = 1,2 104 kg m s-1.
Cette locomotive s’accroche à un wagon, de masse m2 = 1 t,
initialement immobile.
C. Après
l’accrochage, la vitesse du système {locomotive - wagon} a pour
expression : v = m1v1/m2. Faux.
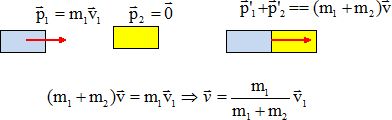
D. La vitesse v du
système {locomotive - wagon} est de 3 m.s-1. Vrai.
3/(3+1) *4 = 3
m.s-1.
Le système
{locomotive - wagon} roule à la vitesse de 5 m.s-1.
Pour s’immobiliser totalement, la locomotive actionne le freinage. Le
système subit alors une force de frottement f constante et
parallèle aux rails de valeur f = 50 N.
E. La distance de
freinage vaut d = 2000 m. Faux.
Variation de l'énergie
cinétique du système : 0-½(m1+m2)v2 ; travail des frottements : -fd.
d= ½(m1+m2)v2
/f = 0,5*4000*52 / 50 =1000 m.
|
Interférences et
différence de marche.
On éclaire deux fentes
distantes de a = 0,53 mm à l’aide d’un faisceau laser vert. On place un
écran à 2 m des fentes pour observer la figure d’interférence.
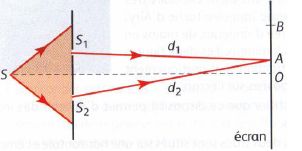
Donnée : λvert=
530 nm.
A. L’interfrange i a pour valeur i =
1.10-3 m. Faux.
i = lD/a =530 10-9*2/(0,53
10-3) =0,002 m.
B. Si on utilise un laser de
longueur d’onde plus grande, l’interfrange augmente. Vrai.
On éclaire, à présent,
ces fentes par une diode laser de longueur d’onde λ = 600 nm et placée
sur l’axe de symétrie du système. On note δ la différence de marche.
Au point A, on mesure δ1
= 1,5 μm.
Au point B, on mesure δ2
= 3,6 μm.
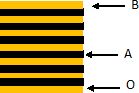
C. En O, on observe une frange
sombre. Faux.
Le laser est sur l'axe de
symétrie SO du système. la frange centrale en O est brillante.
D. En A, on observe une frange
sombre. Vrai.
δ1 = 1,5 μm ;
λ = 0,600 µm ; δ1 =2,5 l.
E. Entre les points A et B, on
compte 3 franges sombres.Vrai.
δ2
= 3,6 μm ; λ = 0,600 µm ; δ2 =6 l. En B
la frange est brillante.
|
|