Propulseur électromagnétique : le
railgun.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Principe.
On considère un circuit électrique rigide.
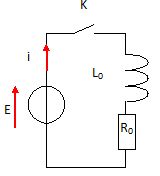 Exprimer le flux
propre à travers le circuit et la fem d'auto-induction.
Exprimer le flux
propre à travers le circuit et la fem d'auto-induction.
F = L0
i ; loi de Faraday : e = -dF/dt
= -d(L0i)/dt.
Le circuit étant indéformable, l'inductance est constante ; par suite :
e = -L0di/dt.
A partir du bilan
énergétique déterminer l'expression de l'énergie électromagnétique Em.
On note I0, l'intensité en régime permanent. Lors de la
fermeture de l'interrupteur K, la bobine introduit un retard à
l'établissement du courant. Elle stocke de l'énergie.
Additivité des tensions : E = R0i + L0di/dt.
Multiplier par i dt : Ei dt = R0i2dt+
L0idi = R0i2dt+
L0d(½i2).
Intégrer par rapport au temps : E I t = R0i2t
+½L0I02.
E I t : énergie fournie par le générateur
; R0i2t : énergie dissipée
par effet Joule ; ½L0I02 :
énergie magnétique.
Le circuit comprend une partie mobile : un barreau peut glisser sans
frottement le long de deux rails parallèles. Aucun champ magnétique
n'est crée par des sources extérieures.
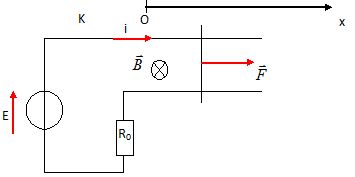
Si
un courant parcourt le circuit, expliquer pourquoi le barreau se met en
mouvement.
Un circuit
parcouru par un courant d'intensité i crée un champ magnétique B. Le
barreau parcouru par un courant et placé dans un champ magnétique B est
soumis à une force de Laplace F.
Le sens de B est donné par la règle de la main droite et F est orientée
dans le sens de l'axe.
Exprimée
la puisance instantanée P fournie par le générateur à la date t en sus
de la puissance Joule.
P = i d F/dt ; F = L i, flux propre.
L n'est pas constante, car le circuit est déformable.
P = i d(Li)/dt = i 2dL/dt +L i di/dt.
Cette puissance est égale à la somme de la variation de l'énergie
magnétique dE m/dt et de la puissance mécanique P méca
fournie au barreau.
Exprimer
la force qui s'exerce sur le barreau.
P = dEm/dt +Pméca ; Em = ½Li2
; dEm/dt = L i di/dt + ½i2
dL/dt.
Pméca = P-dEm/dt =i2dL/dt +L i di/dt - L i di/dt - ½i2 dL/dt.
Pméca == ½i2dL/dt.
On note l l'inductance par
unité de longueur des rails : dL/dt = dL/dx dx/dt = l dx/dt = l v avec v: vitesse du barreau.
Pméca = ½i2 l v.
La puissance mécanique est égale au produit scalaire de la force par la
vitesse : par suite F = ½i2
l .
Le facteur ½ vient du fait que le déplacement est provoqué par le champ
auto-induit.
Une masse de 3,0 g doit
atteindre une vitesse v = 6,0 km/s après un parcours D= 3,0 m. On donne
l =4 10-7
H m-1.
On suppose la force F constante. Calculer l'intensité
i nécessaire.
Les frottements étant négligés, la vitesse initiale étant nulle, le
théorème de l'énergie cinétique conduit à :
½mv2 = FD = ½i2
l D.
i = (mv2 / (lD))½
=(3,0 10-3 *3,6 107 /(4,0 10-7 *3))½
~3,0 105 A.
|
| .
. |
|
|
Modèle
électromécanique du propulseur.
Le projectile porte sur sa partie arrière de minces feuilles de cuivre
qui traversées par une forte intensité fondent rapidement : on est en
présence d'un plasma ( gaz ionisé, conducteur ). Une inductance de stockage L0
est nécessaire car une importante quantité d'énergie soit être
initialement stockée et délivrée rapidement ensuite. La diode évite de
court-circuiter le circuit ( R0, L0) lors de la charge de l'inductance. Lorsque K est ouvert, la diode se comporte comme un interrupteur fermé.
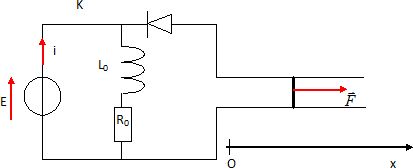
K fermé : un générateur engendre un courant I0 à
travers le circuit (R0, L0). Lorsque cette
intensité est atteinte, on ouvre K à la date t = 0. Le projectile
immobile à l'abscisse x=0 est alors accéléré.
Longueur des rails D = 3 m ; distance des rails d = 0,013 m ; R0
= 160 µW ; L0 = 22 µH ; résistance des rails par unité de longueur : R'=850 µW m-1 ;
résistance du plasma Rp = 500 µW ; I0 = 3 105
A ; masse du projectile m = 3 g.
|
.
|
|
Donner l'équation électrique du circuit. On pose L = L0 + lx et R= R0+Rp +R'x.
K ouvert : d(Li)/dt +R i = 0 ; Ldi/dt + idL/dt +R i = 0 ; (L0+ l x )di/dt + l i dx/dt + R i = 0.
Ecrire l'équation du mouvement du projectile.
Equation mécanique, la seule force qui intervient étant la force de Laplace : m x" = ½l i2.
Conditions initiales : I(t=0) = I0 ; x=0 et x'=0.
Dans le cas ou L0 est très grande, justifier le fait que i(t) ~I0 pendant la phase de propulsion.
Temps caractéristique de décroissance de l'intensité : t = (L0+lx) / R ~L0/R =22 10-6 /((160+850*3+500) 10-6) ~7 ms.
Si la durée de propulsion est inférieure à 1 ms, l'intensité peut être considérée comme constante, égale à I0.
Calculer l'accélération et la vitesse déjection du projectile.
x" = l I02/(2m) =4 10-7 *9 1010 /(2*0,003) = 6 106 m s-2.
v = x"t = 6 106 t ; x = ½x"t2 = 3 106 t2.
Pour x = 3 m, t = 10-3 s et v (t=0,001) =6 103 m/s.
Rendement énergétique du dispositif. On revient au cas général où l'intensité varie au cours du temps.
Quelle est l'énergie DE(t) délivrée depuis l'instant initial par l'inductance de stockage au reste du circuit et au projectile ?
DE(t) est égale à la variation de l'énergie magnétique stockée dans l'inductance L0.
DE(t) =½L0(I20-I2(t)).
Equation électrique du circuit multipliée par i dt : (L0+ l x )idi + l i2 v dt+ R i2 dt= 0.
Intégrer entre 0 et t :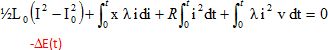
Equation mécanique multipliée par la vitesse v = x' : x" x'= l i2x'/ (2m).
Intégrer entre 0 et t : 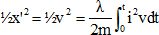
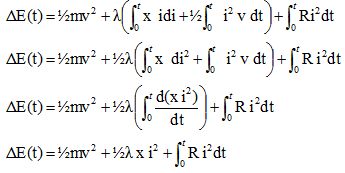
Le terme de gauche correspond à l'énergie fournie au circuit et au projectile.
Le premier terme à droite correspond à l'énergie cinétique du projectile.
Le second terme à droite correspond à l'anergie stockée par auto-induction dans les rails.
Le dernier terme à droite correspond à l'effet Joule.
Dans l'approximation i ~ I0 et pour t = 1 ms, exprimer puis calculer chaque terme.
½mv2 =½m(x"t)2 =0,5 *0,003*(6 106*1 10-3)2 =5,4 104 J.
½lxI02 =0,5 *4 10-7*3*9 1010 =5,4 104 J.
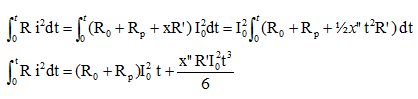
(160 +500)10-6*9 1010*1 10-3 +6 106*850 10-6*9 1010*1 10-9 /6=1,36 105 J.
Quelle est l'intensité i(t= 1 ms) ? Conclure.
DE(t) =½L0(I20-I2(t=1 ms)) = 2*5,4 104 +1,36 105=2,44 105 J.
I20-I2(t=1 ms) =2*2,44 105 /(22 10-6) =2,22 1010.
I2(t=1 ms) =9 1010-2,22 1010 =6,8 1010. I(t=1 ms) = 2,6 105 A. ( 13 % d'écart pr rapport à I0 : l'hypothèse I0 ~constant est valide).
Rendement électromagnétique : ½mv2 / (½L0I02)=5,4 104 / (0,5*22 10-6*9 1010)=0,055 ( 5,5 %).
|
|
|