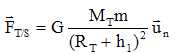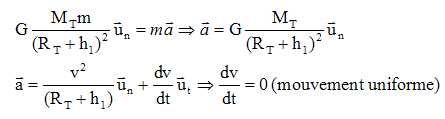Satellite : orbite de transfert. Concours Geipi 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Le satellite de télécommunication Alphasat, le plus grand satellite géostationnaire jamais réalisé en Europe, a été lancé avec succès le 25 juillet 2013 par Arianespace, depuis la base de lancement de Kourou à bord du lanceur Ariane 5. On se propose d’étudier le mouvement d’un tel satellite représenté par le point S autour de la Terre de centre T. 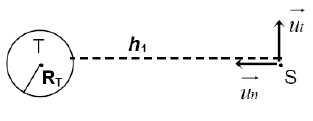Les pointillés définissant h  ont été légèrement décalés vers le haut pour améliorer la lisibilité de la figure Données : Masse de la Terre : MT = 6,0.1024 kg. Rayon de la Terre : RT = 6,4.103 km. Constante de gravitation universelle : G = 6,67. 10-11 kg-1.m3.s-2. Masse du satellite : m = 700 kg L’altitude est notée h de façon générale  Dans quel référentiel doit-on se placer pour faire l’étude du mouvement du satellite ? L'étude du mouvement du satellite est réalisée dans le référentiel géocentrique. On considère que le satellite évolue sur une première orbite circulaire d’altitude basse. Son altitude est notée h1. Donner l’expression vectorielle de la force exercée par la terre sur le satellite en utilisant la base de Frénet en fonction des données de l’énoncé et de h1. 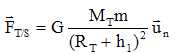En appliquant la 2ème loi de Newton, donner l’expression de l’accélération de S dans la base de Frénet, en fonction des données du problème. Justifier que le mouvement du satellite est uniforme. 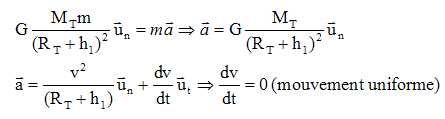En déduire l’expression de la vitesse v1 du satellite en fonction des données de l’énoncé et de h1. Faire l’application numérique pour l’altitude h1= 200 km. 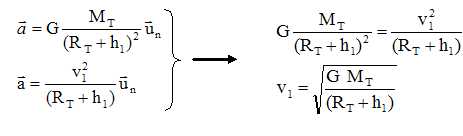v1 = (6,67. 10-11 * 6,0.1024 /(6,4.103 +200)103))½ =7,8 103 m/s. . . Dans le cas d’une trajectoire elliptique autour de la Terre, la période de révolution T d’un satellite est lié à la longueur L du demi-grand axe de son orbite par la relation : T 2 = k. L3 où k = 9,86 10-14 s2.m-3. Si l’orbite est circulaire, on prend L égal au rayon dans la relation donnée précédemment. 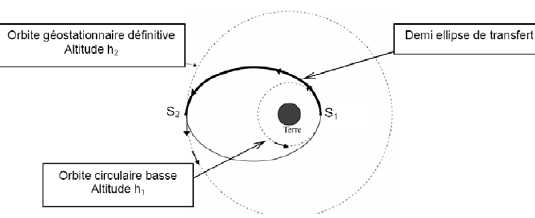Afin de mettre le satellite en orbite géostationnaire, on lui communique un surplus d’énergie en S1. Il va alors décrire une demi-ellipse le long du chemin fléché de S1 vers S2  avant d’être stabilisé sur l’orbite circulaire définitive. . Sachant que la période de révolution T2 du satellite sur son orbite définitive est de 23h 56min 4s, donner l’expression de l’altitude h2 du satellite sur son orbite circulaire définitive en fonction de k et des données de l’énoncé. Faire l’application numérique. T22 = k(RT+h2)3 ; RT+h2 = (T22 / k)1/3 ; h2 =(T22 / k)1/3 - RT. T2 = 23*3600+56*60+4 =8,6284 104 s. h2 =((8,6284 104 )2/ (9,86 10-14))1/3 -6,4 106 =3,6 107 m.. Donner l’expression de la longueur du segment S1S2 en fonction de h1, h2 et des données de l’énoncé. Faire l’application numérique. S1S2 =2RT +h1 + h2 = 2*6,4 106 +2,00 105 +3,6 107 =4,9 107 m. Soit L’, le demi grand axe de l’ellipse de transfert tel que S1S2 = 2L'.  En déduire la durée Dt du transfert de S1 vers S2. Donner son expression littérale et faire l’application numérique. Le satellite parcourt la moitié de l'ellipse entre S1 et S2. La durée du parcourt est la moitié de la période de révolution T sur l'ellipse. Dt = ½(kL3)½ =0,5(9,86 10-14(4,9 107/2)3)½ =1,9 104 s ou  5h 17 min. Justifier que la vitesse du satellite diminue au cours du transfert. Loi des aires : le segment de droite reliant les centres de gravité de la terre et du satellite balaie des aires égales pendant des durées égales : la vitesse sera plus grande quand le satellite est  plus proche de la Terre.  En fin de transfert en S2, la vitesse vaut 1602 m/s. Afin que le satellite se stabilise sur son orbite circulaire définitive, que faut-il faire en S2 ? Pour rester sur l'orbite circulaire à l'altitude h2, la vitesse du satellite doit être : v2 = (6,67. 10-11 * 6,0.1024 /(6,4.103 +3,6 104)103))½ =3,1 103 m/s. Il faut donc accélérer en S2.

menu