Plan
incliné : énergie, travail, puissance. Concours Geipi 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
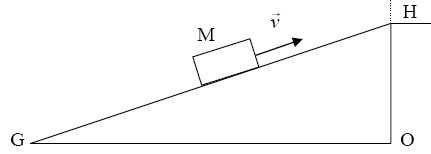
Lors de déménagements,
il est fréquent de voir l'utilisation d'un monte-meubles, sorte de
tapis roulant incliné qui entraîne meubles et cartons à la hauteur
voulue. Ainsi, afin d'équiper un appartement situé au 3ème
étage d'un immeuble récent, on peut utiliser un tapis roulant de 20,10
m de long dont le sommet se trouvera à 9,30 m de hauteur, au bord d'une
fenêtre de l'appartement. La situation est schématisée par la figure
ci-dessous.
Un carton de livres de masse M=40,00 kg, qu'on assimilera à son centre
de gravité, est entraîné par le tapis roulant à vitesse constante v=
0,50 m/s.
.
Donner
les longueurs des segments GH et OH. En déduire la distance GO,
distance nécessaire entre le bas du monte-meubles et l'immeuble.
GH = 20,10 m ; OH = 9,30 m ; OG =(GH2-OH2)½
=(20,102-9,302)½=17,82
~17,8 m.
Montrer
que l'angle d'inclinaison du tapis avec le sol est de 27,56 °.
sin a =
OH / GH = 9,30 / 20,10 =0,463 ; a
= 27,56°.
Evaluer
l'énergie cinétique de la masse M au point G et au point H.
La vitesse étant constante, l'énergie cinétique reste constante :½Mv2
= 0,5*40,0 *0,502=5,0 J.
Le point G est considéré à l'altitude nulle et l'origine de l'énergie
potentielle de pesanteur est choisie à cette altitude. Calculer
l'énergie potentielle de pesanteur de la masse M au point H.
Ep = MgOH = 40,0*9,81*9,30 =3,65 103 J.
Donner
les expressions et les valeurs de l'énergie mécanique Em de la
masse M au point G et au point H.
Au point G, l'énergie mécanique est sous forme cinétique : Em(G)
= ½Mv2.
Au point H, l'énergie mécanique est sous formecinétique et potentielle
de pesanteur : Em(H)
= ½Mv2+MgOH.
Calculer
la variation de l'énergie mécanique de la masse M lors de son
déplacement entre G et H. Cette variation d'énergie correspond-elle à
un travail moteur ou à un travail résistant ou ne peut-elle pas être
attribuée au travail d'une force ?
Em(H)-Em(G)
= MgOH, valeur positive.
Cette variation d'énergie correspond à un travail moteur, l'opposé du
travail du poids.
Justifier
que la somme des forces s'exerçant sur M est nulle.
Le mouvement est rectiligne uniforme ; d'après le principe d'inertie,
le système est pseudo-isolé ( la somme vectorielle des forces appliquée
au carton est nulle ).
|
| .
. |
|
|
Deux forces s'appliquent à la masse M,
son poids P et la force due au tapis F..
Représenter ces forces sur le schéma.
Montrer, par construction, que la force F est la somme d'une force R
perpendiculaire au tapis et d'une force f parallèle au tapis
dont les modules sont donnés par R = M g cos (27,56°) et f = M g sin
(27,56°). Calculer les modules de ces forces.
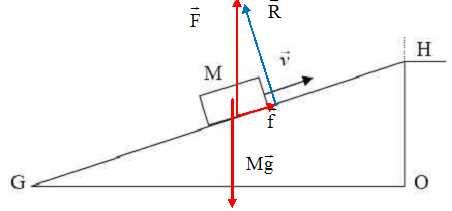
R = 40,0*9,81*cos 27,56=348 N ; f = 40,0*9,81*sin 27,56=182 N.
|
.
|
|
Donner les
expressions du travail des forces P, R et f au cours
du déplacement de la masse M de G à H. Calculer leurs valeurs numériques.
R, perpendiculaire à la vitesse ne travaille pas.
Travail de f : f * GH = 182*20,10 =3,65 103 J.
Travail résistant du poids en montée : -MgOH = -40,0*9,81*9,30 = -3,65
103 J.
Comparer
la variation d'énergie mécanique de la masse M entre G et H aux
résultats trouvés à la question précédente. Conclusion.
L'énergie mécanique augmente du travail moteur de la force f.
Evaluer la
durée t
du trajet G à H pour la masse M. Quelle est la puissance mécanique
nécessaire, Pu pour entraîner le tapis lors de
ce trajet ?
t
= GH / v = 20,10 /0,50 = 40,2 s.
Pu = valeur de la force f fois vitesse = f v =
182*0,50 = 91 W.
|
|
|

