Cavité optique, miroirs
sphériques.
Concours inspecteur Dgccrf
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
On
considère, dans les conditions de Gauss, un système optique centré
constitué de deux miroirs sphériques concaves, de même axe optique,
notés respectivement M 1 ( centre C 1, sommet S 1, rayon R 1 = C 1S 1 >0 ) et M 2 ( centre C2, sommet S2, rayon R2 = S2C2 >0 ) et L = S2S1>0.
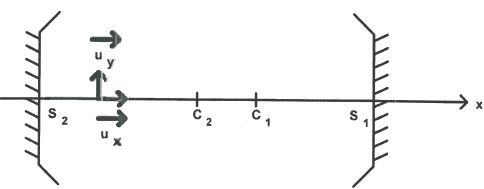
On se propose d'étudier les allers-retours des rayons lumineux au sein
de cette cavité en se limitant à ceux appartenant à un plan
d'invariance par rotation du système. Tout point dans un tel plan, est
alors repéré par ses coordonnées longitudinale x et transversale y.
Les vecteurs sont écrits en gras et en bleu.
Un rayon lumineux, noté r0, de vecteur unitaire associé u0, se réfléchit en un point I0 du miroir M1 de coordonnée transversale y0 donnant ainsi naissance à un rayon réfléchi, noté r'0, de vecteur unitaire associé u'0.
On pose a0 = (ux, u0) et a'0 = (-ux, u'0).
Montrer que a'0 = 2y0/R1 -a0.
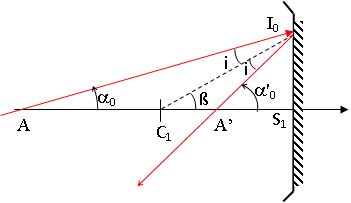
Dans les triangles AI0C1 et C1I0A', les sommes des angles donnent :
a0 +i +p-ß = i +ß+p-a'0 soit a0 +a'0 =2ß.
Dans les conditions de Gauss, les angles sont petits et tan ß ~ß ~y0/R1.
a0 +a'0 ~2y0/R1.
Le rayon r'0 se réfléchit sur le miroir M2 en un point I'0 de coordonnée transversale y'0 donnant naissance à un rayon réfléchi, noté r1, de vecteur unitaire u1.
Montrer que y'0 = y0-La'0.
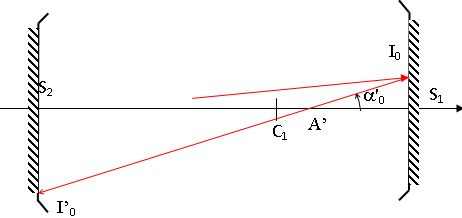
a'0 ~S1I0 / A'S1 ; a'0 A'S1 ~y0 et a'0 ~I0S2 / S2A' ; a'0 S2 A' ~ -y'0 ;
a'0 A'S1 +a'0 S2 A' =a'0 L ~y0 -y'0.
|
| .
. |
|
|
On notera a1 =(ux, u1).
Montrer que a1 = -2y'0/R2-a'0.
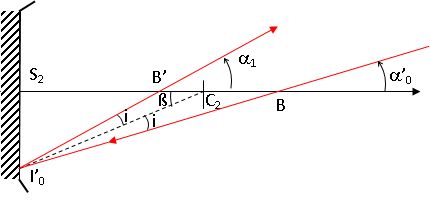
Dans les triangles BI'0C2 et C2I'0B', les sommes des angles donnent :
a'0 +i +p-ß = i +ß+p-a1 soit a1 +a'0 =2ß.
Dans les conditions de Gauss, les angles sont petits et tan ß ~ß ~-y0/R2.
a1 +a'0 ~ -2y'0/R2.
Soit I1, de coordonnée transversale y1, le point du miroir M1 où le rayon r1 vient se réfléchir.
En déduire la matrice 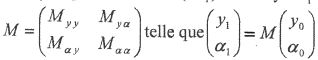 . .
a1 ~S1I1 / BS1 ; a1 BS1 ~y1 et a1 ~I'0S2 / S2B ; a1 S2 B ~ -y'0 ;
a1 BS1 +a1 S2 B =a1 L ~y1 -y'0 ; y1 = a1 L+y'0.
y1 = -(a'0 +2y'0/R2 )L+y'0= -a'0L+y'0(1-2L/R2)=-a'0L+(y0-La'0)(1-2L/R2)= -2a'0L(1-L/R2)+y0(1-2L/R2).
y1 =-2L(2y0/R1-a0)(1-L/R2)+y0(1-2L/R2).
y1 = (1-2L/R2-4 L/R1(1-L/R2))y0 + a0 ( 2L(1-L/R2)).
On identifie : Myy =1-2L/R2-4 L/R1(1-L/R2) et Mya =2L(1-L/R2).
a1 = -a'0 -2y'0/R2 = -a'0 -2(y0-La'0)/R2 = -2y0 /R2 -a'0 (1-2L/R2)= -2y0/R2-(2y0/R1 -a0)(1-2L/R2).
a1 =(1-2L/R2)a0 -2y0( 1/R2+1/R1(1-2L/R2)).
On identifie : May= -2( 1/R2+1/R1(1-2L/R2)) et Maa =(1-2L/R2).
Déterminer la dimension de chaque coeficient de la matrice M.
Myy et Maa sont sans dimension ; Mya a la dimension d'une longueur ; May est l'inverse d'une longueur.
|
.
|
|
Une
cavité est dite stable si tout rayon lumineux au voisnage de l'axe
reste, après multiples réflexions, confiné au voisinage de l'axe.
On étudie le cas particulier L = R1=R2.
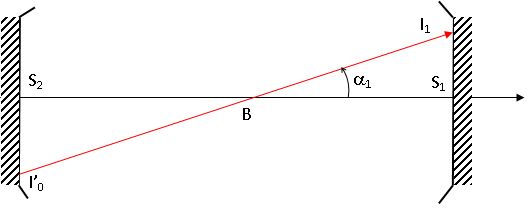
Vérifier que :  . .
Myy =1-2L/R2-4 L/R1(1-L/R2) =1-2-0 = -1 et Mya =2L(1-L/R2) = -2L(1-1)=0.
May= -2( 1/R2+1/R1(1-2L/R2)) =-2/L(1+1-2) =0 et Maa =(1-2L/R2)=1-2=-1.
Décrire
l'évolution au sein de la cavité, d'un rayon incident parallèle à l'axe
optique puis d'un rayon incident, incliné par rapport à l'axe optique,
passant par le milieu du segment [S1S2].
Un
rayon incident parallèle à l'axe optique se réfléchit en passant par le
foyer F du miroir sphérique. Un rayon incident passant par le foyer F
est réfléchi parallèlement à l'axe optique.
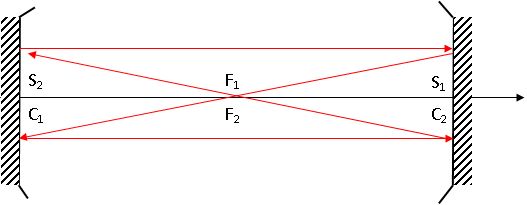
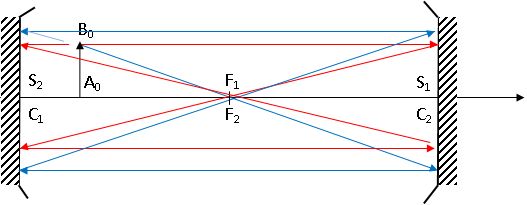
Soit un objet transversal de petite taille noté A0B0, A0 appartenant au segment [S1S2].
Déterminer son image après 2n réfexions dans la cavité ainsi que le grandissement correspondant.
Le
grandissement est égal à +1 ; après deux aller et retour dans la cavité
( soit un nombre pair de réflexions sur chaque miroir), l'image
coïncide avec l'objet, la cavité est stable.
Soit le cas particulier L = ½R1 = ½R2.
Simplifier l'expression de la matrice M.
Myy =1-2L/R2-4 L/R1(1-L/R2) =1-2*0,5-4*0,5(1-0,5)= -1 et Mya =2L(1-L/R2) = 2L(1-0,5)= L.
May= -2( 1/R2+1/R1(1-2L/R2)) =-1/L(1+1-1) =-1/L et Maa =(1-2L/R2)=1-1=0.
Calculer M3.
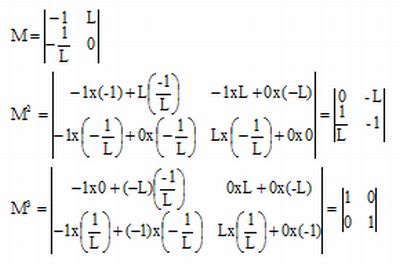
Cette cavité est-elle stable ? On pourra dterminer graphiquement l'image d'un objet transversal A0B0 après multiples réflexions sur les miroirs.
M3 est la matrice unité, cette cavité est stable.
|
|
|