Chauffe-eau
solaire : pertes thermiques dans le ballon, dynamique des fluides,
protection contre la corrosion : bts Travaux publics 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
|
|
|
|
|
Installation
d'un chauffe-eau solaire.
En
vue d’économiser l’énergie utilisée pour la production d’eau chaude
sanitaire, de nombreuses constructions optent pour l’installation d’un
chauffe-eau solaire. Un tel chauffe eau est composé :
· De capteurs solaires qui transmettent le rayonnement solaire direct
et diffus sous forme de chaleur.
· D’un ballon de stockage de l’eau chaude sanitaire.
· D’une pompe qui assure la circulation du fluide caloporteur jusqu’à
la cuve de stockage de l’eau.
· D’un régulateur qui gère l’appoint nécessaire pour les périodes de
faible ensoleillement (par l’intermédiaire d’une chaudière à
condensation).
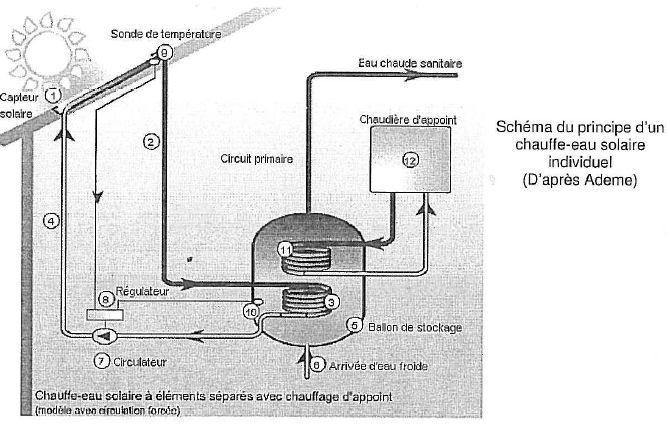 Étude des
déperditions thermiques dans le ballon.
Étude des
déperditions thermiques dans le ballon.
Ce réservoir contient deux échangeur de chaleur : l’un pour l’apport
solaire, l’autre pour l’appoint. Il a une capacité de 300 litres, ce
qui permet d’assurer 70% des besoins annuels d’eau chaude sanitaire
pour une famille de cinq personnes. L’isolation thermique est garantie
par une mousse isolante de 100 mm d’épaisseur.
Le ballon a une capacité de remplissage en eau de 300 litres, une
hauteur H = 1,65 m et un diamètre D = 0,70 m. Par une journée
ensoleillée (même en septembre), les capteurs solaires élèvent la
température de l’eau dans le ballon.
Le ballon est posé sur le sol car sa masse totale est de 460 kg, sa
base ne participe pas aux échanges de chaleur.
La ventilation du local dans lequel le ballon est placé assure une
température extérieure uniforme.
Données
: masse volumique de l’eau r
= 1,0.103 kg.m-3 ; capacité thermique massique de
l’eau C = 4,18.103 J.kg-1.°C -1 ;
conversion kilowattheure 1kW.h = 3,6.106 J.
|
|
|
Étude
des pertes thermiques par conduction dans le ballon au cours d’une nuit.
L’isolation thermique du
ballon est due à une enveloppe amovible en mousse d’épaisseur e = 100
mm et de
conductivité thermique l
= 8,0.10-2 W.m-1.K-1. On suppose que
la température de l’eau dans le ballon vaut 75°C et que la température
extérieure est de 18°C.
On dispose au laboratoire du matériel suivant : thermomètres avec
sonde, multimètre, chronomètre, source lumineuse blanche, vase en
aluminium de 500 mL et couvercle, plaque de polystyrène expansé de 1,0
cm d’épaisseur, cristallisoir en verre, thermoplongeur, alimentation
stabilisée de 6V, rouleaux de mousse de différentes épaisseurs (0,5 cm,
1,0 cm et 1,5 cm).
En choisissant le matériel adapté, proposer
une expérience permettant de mettre en évidence l’influence d’une
augmentation d’épaisseur de la mousse sur la diminution des pertes
thermiques par conduction au sein du ballon d’eau chaude.
Dans un vase en aluminium de 500 mL avec couvercle introduire 200 mL
d'eau du robinet et y plonger le thermoplongeur relié à l'alimentation
stabilisée, ainsi qu'un thermomètre. Chauffer l'eau à 30 °C.
Chronométrer la durée au bout de laquelle la température du système
diminue de 1°C.
Recommencer plusieurs fois l'expérience en modifiant à chaque fois
l'épaisseur de l'isolant autour du vase.
Rappeler
l’expression de la loi reliant la densité de flux thermique par
mètre carré, F, la différence de
température Dq et la résistance thermique R.
F =Dq / R.
Montrer
que le flux thermique par mètre carré a pour valeur 4,6.101
W.m-2.
R = e / l = 0,100 / (8,0.10-2) =1,25 m2 K W-1.
F =Dq / R =(75-18) / 1,25 =45,6
~46 W m-2.
Vérifier que la
valeur de la surface de contact entre le chauffe-eau et l’air est
S = 4,0 m2.
Surface latérale du ballon cylindrique : p D H =3,14 *0.70 *1,65 =3,63 m2.
Surface de la partie supérieure : pD2/4
=3,14 *0,702/4 =0,39 m2 ; total =4,0 m2.
Calculer
le flux thermique F.
45,6*4,0 = 182,4 ~1,8 102 W.
Détermination
de la chute de température de l’eau dans le ballon la nuit.
On suppose que la diminution de la température de l’eau dans le ballon
est due uniquement aux pertes par conduction. On considère qu’une nuit
dure 12 heures et que la température extérieure au ballon reste égale à
18°C.
Montrer
que la quantité de chaleur Q perdue par l’eau chaude en une nuit vaut
7,8.106 J. On suppose que le flux thermique reste égal à F, valeur calculée ci-dessus.
Q = F Dt = 182,4 *12 = 2,189
kWh ou 2,189*3,6 106 ~7,8.106 J.
En déduire la chute
de température DT de l’eau dans le
ballon.
Q = m c DT ; DT = Q / (mc) = 7,8 106(
300*4180)= 6,3°C.
|
.
|
|
Étude de la
station solaire.
Elle est constituée d’une pompe électrique, des thermomètres pour
observer les températures dans les conduites aller et retour, d’un
manomètre et des soupapes de sécurité. Nous étudierons la circulation
du fluide caloporteur.
La station contient la pompe (appelée
circulateur) chargée de faire circuler le fluide caloporteur entre les
panneaux solaires et le ballon d’eau chaude. Son débit volumique
optimal est QV = 20 L.min-1, le
diamètre des canalisations est 15 mm.
Données :
accélération de la pesanteur : g = 9,8 m.s-2. 1
bar = 1,0.105 Pa.
Pour
un fluide en écoulement permanent entre 2 points 1 et 2, échangeant
avec une machine une puissance P, l'équation de conservation de
l’énergie dans une installation hydraulique est donnée par la relation :
½r(v22-v12)
+(p2-p1) +rg(h2-h1)
= Pu / Qv, où Qv est le débit
volumique et Pu la puissance utile de la machine.
Étude du débit du
fluide caloporteur.
Calculer
le débit massique Qm.
Qv = 0,020 /60 =3,33
10-4 m3/s ; Qm
= r QV
=1000*3,33 10-4 =0,3333
~0,33 kg s-1.
Calculer la vitesse
moyenne du fluide caloporteur en régime permanent.
vmoy = Qv
/ section canalisation =3,33
10-4 /(3,14*0,0152/4) =
1,886 ~1,9 m/s.
Si
la pompe ne fonctionne pas, quelle est la
différence de pression du fluide entre la pompe et les panneaux sachant
qu’on peut estimer la hauteur moyenne entre les deux à 7,0 m ?
(1) : panneaux ; (2) ballon (
altidude h2 = 0).
p2-p1= rg(h1-h2)] =1000*9,81*7,0 = 68670 ~6,9 104
Pa = 0,69 bar
Détermination de
la puissance utile du circulateur.
Lorsque la pompe fonctionne, un manomètre indique un l’écart de
pression entre la pompe et les panneaux solaires égal à 2,0 bars.
Calculer
la puissance utile de la pompe.
On suppose que la vitesse du fluide dans le ballon est proche de zéro.
(1) : panneaux ; (2) ballon.
Pu =
Qv[½r(v22-v12)
+(p2-p1) +rg(h2-h1)]
= 3,33 10-4 [-500*1,8862+2,0
105 +1000*9,81(0-7) ] =43 W.
|
Protection du
ballon contre la corrosion.
La protection anti-corrosion du ballon est assurée par un double
émaillage et la présence d’une anode en magnésium. Elle garantit une
meilleure qualité de l’eau chaude sanitaire et une durée de vie
optimale de l’installation.
Cette
protection est assurée par un double émaillage du fer constituant la
carcasse du ballon et par le contact de cette carcasse avec une anode
en magnésium.
On plonge un clou en fer décapé dans un bécher contenant une solution
de chlorure de sodium à 3% à laquelle on ajoute une petite quantité de
solution de ferricyanure de potassium. Au bout de quelques heures on
observe une
coloration bleue dans la solution. Si on réalise la même expérience en
ajoutant dans le bécher une plaque de zinc que l’on relie par un fil
métallique au clou, cette coloration ne se constate plus. En revanche
on mesure un
courant électrique dans le fil métallique dans le sens fer-zinc.
Sachant que les ions ferricyanure réagissent avec les ions Fe2+ pour former un précipité bleu, expliquer en quoi ces deux expériences mettent en évidence le principe de la protection par anode sacrificielle ?
Le fer s'oxyde en milieu humide en présence de dioxygène : il se forme des ions Fe2+ qui vont réagir avec les ions ferricyanure.
Le zinc est plus réducteur que le fer ; le zinc s'oxyde à la place du fer et ce dernier est protégé contre la corrosion.
Quel
autre métal parmi le plomb, l’aluminium ou le cuivre pourrait remplacer
le magnésium pour protéger le ballon en supposant que celui-ci est
intégralement en fer ? Justifier la réponse.
E°(Zn2+/Zn) = -0,76 V ; E°(Cu2+/Cu) = 0,34 V ; E°(Al3+/Al) = -1,66 V ; E°(Fe2+/Fe) = -0,44 V ; E°(Mg2+/Mg) = -2,37 V ; E°(Pb2+/Pb) = -0,13 V.
Les métaux plus réducteurs ( E°(Mn+/ M )< E°(Fe2+/Fe) ) que le fer conviennent : zinc, aluminium, magnésium.
Écrire la demi-équation d’oxydation du magnésium.
Mg = Mg2+ +2e-.
L’espèce responsable de cette oxydation est le dioxygène, dissout dans
l’eau du robinet, appartenant au couple d’oxydoréduction O2/H2O dont la demiéquation est
½O2 + 2H+ +2e- = H2O.
Écrire l’équation - bilan modélisant l’oxydation du magnésium par le dioxygène.
½O2 + 2H+ +Mg = Mg2+ + H2O.
L’intensité du courant de corrosion est estimée à 25 mA, calculer
la durée d’utilisation de l’électrode de magnésium si sa masse est de
800 g. Exprimer le résultat en seconde puis en année.
Données : · Masse molaire du magnésium : M (Mg)= 24,0 g.mol-1.· Relation entre intensité et charge électrique : I Dt = nF ; n : quantité de matière d'électron et F = 96500 C mol-1.
Quantité de matière de magnésium : nMg = m / M(Mg) = 800 / 24,0 =33,33 mol ; n= 2nMg =66,67 mol.
Dt = nF / I = 66,67 *96500 / 0,025 = 2,57 108 s ~ 2,57 108 /(3600*24*365)=8,2 années.
En réalité, l’agent de maintenance change l’électrode de magnésium au bout de 5 ans. Il constate, en observant l’électrode usagée, qu’elle est recouverte d’une pellicule solide blanche de carbonate de calcium appelée calcaire.
Proposer une explication pour justifier la présence de ce dépôt solide.
L'eau du robinet contient des ions Ca2+ et hydrogénocarbonate HCO3-. Ces ions réagissent entre eux pour donner du calcaire CaCO3(s)
Ca2+ aq + 2HCO3-aq = CaCO3(s) + CO2(g)+ H2O.
Le carbonate de calcium est très peu soluble : 10 mg/L à 50 °C. Il se dépose donc sur le magnésium.
|
|