Mathématiques : équation différentielle, étude de fonction, calcul intégral, probabilité ( groupe B), bts 2012.

Mathématiques : équation différentielle, étude de fonction, calcul intégral, probabilité ( groupe B), bts 2012.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.

Résolution d'une équation différentielle.
On considère l'équation différentielle (E) : y' +2 y = -5 exp(-2x)
où y est une fonction inconnue de la variable x, définie et dérivable sur R et y' sa fonction dérivée.
Déterminer les solutions de l'équation différentielle (E₀) :
y' +2 y =0.
On recherche une solution générale du type : y= A exp(B x) où A et B sont des constantes.
Dériver : y' = AB exp((B x).
Repport dans E₀ : AB exp((B x)+2 A exp(B x)=0.
A exp(B x) (B+2) = 0 ; par suite B = -2.
y = A exp(-2 x).
Soit g la fonction définie sur R par g(x) = -5x exp(-2x).
Démontrer que la fonction g est une solution de (E).
On pose : u = -5x ; v =exp(-2x) ; u'=-5 ; v' = -2 exp(-2x).
Dérivée d'un produit : g' = u'v+v'u =-5 exp(-2x)+10x exp(-2x) = 5 exp(-2x) (-1+2x).
Repport dans (E) : 5 exp(-2x) (-1+2x) -10x exp(-2x) = -5 exp(-2x).
Simplifier : -5 exp(-2x)= -5 exp(-2x), égalité vrai quel que soit x.
repport dans (E) : 0 +0,25 x =0,25 x est vérifiée quel que soit x.
g(x) est bien une solution de (E).
En déduire les solutions de (E).
Les solutions de (E) sont obtenues en faisant la somme des solutions de (E₀) et d'une solution particulière de (E) :
y = A exp(-2 x) -5x exp(-2x) = (A-5x) exp(-2x).
Déterminer la solution f de l'équation différentielle (E) qui vérifie la condition initiale f(0)=1.
f(0) = A exp(0) = 1 d'où A = 1.
f(x) = (1-5x) exp(-2x).
Etude locale d'une fonction.
Soit la fonction définie sur R par f(x) = f(x) = (1-5x) exp(-2x).
On désigne par C la courbe représentative de f dans un repère (O, i, j) orthogonal.
On admet le résultat suivant : la limite de -5x exp(-2x) vaut zéro quand x tend vers l'infini.
Quelle est la limite de f(x) quand x tend vers l'infini ?
-5x exp(-2x) tend vers zéro et exp(-2x) tend également vers zéro quand x devient très grand.
Par suite f(x) tend vers zéro lorsque x devient très grand.
On peut encore dire que la droite d'équation y = 0 est asymptote à la courbe C quand x tend vers l'infini.

.
.

Le développement limité à l'ordre 2, au voisinage de zéro, de la fonction h(x) = esp(x) est :
h(t) = 1 +t +½t² + t²e(t).
Déterminer le développement limité, à l'ordre 2, au voisinage de zéro, de la fonction exp(-2x).
Remplacer t par -2x dans le développement précédent.
g(x) = 1 -2x +2x² + x²e(x).
En déduire que le développement limité, à l'ordre 2, au voisinage de zéro, de la fonction f est :
f(x) = 1-7x+12x²+ x²e(x).
f(x) = (1-5x) ( 1 -2x +2x² + x²e(x)).
f(x) = 1 -2x +2x² -5x +10x² + x²e(x)).
f(x) = 1 -7x +10x² + x²e(x)).
En déduire une équation de la tangente T à la courbe C au point d'abscisse x=0.
y = 1-7x.
Etudier la position relative de T et C au voisinage du point d'abscisse 0, pour x positif.
Au voisinage de zéro, f(x)-y = +10 x² avec x positif.
f(x)-y est positif ; f(x) > y : la tangente est située en dessous de la courbe C.

.

Calcul intégral.
On note 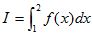où f est définie dans la partie précédente.
Démontrer, à l'aide d'une intégration par partie, que I = (23 e^-4-13e^-2) / 4.
On pose : u = 1-5x ; v ' =exp(-2x) ; u'= -5 ; v = -½ exp(-2x).

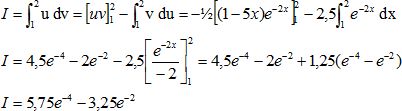
Donner la valeur approchée de I à 0,01 près.
I = 5,75 *0,01831 -3,25*0,1353= -0,33.
Donner, sans justification, le signe de f(x) pour x dans l'intervalle [1, 2].
Le terme en exponentielle est positif et (1-5x) est négatif : f(x) est donc négative.
Interpréter graphiquement le nombre I.
I est l'aire ( exprimée en unité d'aire) comprise entre la courbe C et l'axe horizontal, comptée négativement.
Loi normale.
On prélève au hasard une botte de paille dans la production du 20 juillet 2011.
On désigne par X la variable aléatoire qui, à chaque botte, associe son épaisseur exprimée en mm. On admet que X suit la loi normale de moyenne 360 et d'écart type 18.
Déterminer la probabilité P(350 <= X <=370).
X suit la loi normale N(m=360, s=18).
p(350<=X<=370) = p(-10 / 18 < = (X-m) / s <=10 / 18)
(Y-m) / s suit la loi normale centrée réduite : 2P(10/18)-1 ~2 P(0,56)-1.
Les tables donnent :

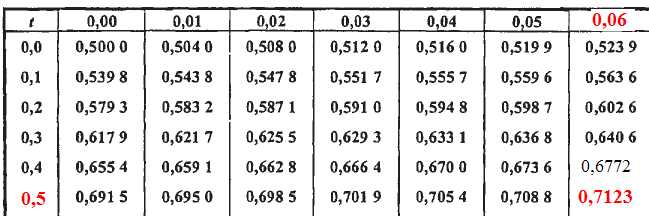
p(350<=X<=370) =2*0,7123-1 =0,4246 ~0,43.
On désigne par Y la variable aléatoire qui, à chaque botte, associe sa densité exprimée en kg m^-3. On admet que Y suit la loi normale de moyenne 100 et d'écart type 5.
Déterminer la probabilité P(90 <= Y <=110).
Y suit la loi normale N(m=100, s=5).
p(90<=X<=110) = p(-10 / 5 < = (X-m) / s <=10 / 5)
(Y-m) / s suit la loi normale centrée réduite : 2P(2)-1=2*0,9772-1 =0,9544 ~0,95.
On suppose que les variables X et Y sont indépendantes. Une botte de paille est conforme aux normes d'isolation si son épaisseur, exprimée en mm, appartient à l'intervalle [350, 370] et si sa densité, exprimée en kg m^-3, appartient à l'intervalle [90 ; 110 ].
Calculer la probabilité qu'une botte prélevée dans la production de cette journée soit conforme aux normes d'isolation.
Les deux varaibles X et Y étant indépendantes : p(conforme) = 0,4246 * 0,9544 =0,4052 ~0,41.

Loi binomiale.
On considère un stock important de bottes de paille, dont une partie est destinée à un usage d'isolation. On note E l'évenement " une botte de paille prélevée au hasard dans le stock est conforme aux normes d'isolation". On suppose que P(E) = 0,4. On prélève au hasard 5 bottes de paille dans le stock pour vérification de la conformité aux normes. Le stock est suffisamment important pour que l'on puisse assimiler ce prélevement à un tirage avec remise de 5 bottes. On considère la variable aléatoire Z qui a tout prélevement ainsi défini, associe le nombre de bottes qui sont conformes pour la longueur.
Justifier que Z suit une loi binomiale dont on précisera les paramètres.
Les prélevements sont indépendants et leur nombre est fixé à n = 5. La probabilité qu'une botte soit conforme est constante p = 0,4.
La loi binomiale B(n=5, p = 0,43) est valide.
Calculer la probabilité P(Z=5). Toutes les bottes sont conformes aux normes.
P(Z=5) = 0,4⁵ =0,01024 ~0,010.
Calculer la probabilité que dans un tel prélevement au moins 4 bottes soient conformes aux normes.
"au moins 4" signifie 4 ou 5.
P(Z=4)=C₅⁴ p⁴ q avec C₅⁴ =5*4*3*2 / (4*3*2)=5 ; p=0,4 et q = 0,6.
P(Z=4)=5*0,4⁴*0,6=0,0768.
P(Z=5) +P(Z=4)=0,01024 + 0,0768 ~ 0,087.
Intervalle de confiance.
On prélève au hasard 50 bottes de paille dans la production du 22 juillet 2011. La production est assez importante pour que l'on puisse assimiler ce prélèvement à un tirage avec remise. On constate que 37 bottes de cet échantillon sont conformes aux normes.
Donner une estimation ponctuelle de la fréquence inconnue p des bottes de paille de cette production qui sont conformes aux normes.
p =37/50 = 0,74.
Soit F la variable aléatoire qui, à tout échantillon de 50 bottes ainsi prélevé, associe la fréquence des bottes de cet échantillon qui sont conformes aux normes d'isolation.
On suppose que F suit la loi normale de moyenne inconnue p et d'écart type s=(p(1-p)/50)^½ = (0,74(1-0,74)/50)^½ =0,062.
Déterminer l'intervalle de confiance de la fréquence p au niveau de confiance de 95 % ?
F suit la loi normale N(p, s).
F₀=(F-p) / s suit la loi normale centrée réduite.
p(-t < F₀ < t) =0,95 ; 2P(t)-1 =0,95 ; P(t) =1,95/2 = 0,975.
Les tables donnent t = 1,96.

L'intervalle de confiance est donc : [p-1,96 s ; p+1,96 s ] soit [0,74-1,96*0,062 ; 0,74+1,96*0,062] ; [ 0,62 ; 0,86].
On considère l'affirmation suivante : " la fréquence p est obligatoirement dans cet intervalle de confiance".
Cette affirmation est-elle vraie ?
Cette affirmation est fausse. Dans 95 % des cas, p se trouve dans cet intervalle de confiance.

menu