Un peu de
balistique : bac
S Amérique du Sud 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Lors
de fouilles préventives sur un chantier de travaux publics, on a
retrouvé ce qui ressemble à une arme à
feu. Il s’agit d’un ancien pistolet lance-fusées en bronze datant
probablement de la première Guerre Mondiale. Il
est dans un état de conservation assez remarquable. Ce type de pistolet
était très utilisé lors de cette guerre car, en plus de lancer des
fusées éclairantes, il pouvait servir de moyen de communication. En
effet, à l’époque très peu de moyens étaient mis à disposition des
troupes : les ondes hertziennes étaient très peu utilisées et c’étaient
des kilomètres de câbles téléphoniques qui devaient être déroulés pour
permettre la transmission de messages divers et variés.
Ainsi les pistolets signaleurs se sont avérés très utiles.
Durée de
visibilité de la fusée.
Sur la notice des fusées éclairantes que l’on peut utiliser dans ce
type de pistolet, on trouve les informations
suivantes : Cartouche qui lance une fusée éclairante s’allumant 1,0
seconde après son départ du pistolet et éclaire d’une façon intense
pendant 6 secondes environ. Masse de la fusée éclairante : mf
= 58 g.
On se place dans le référentiel terrestre supposé galiléen. Le champ de
pesanteur terrestre est considéré uniforme, de valeur g = 9,8 m.s−2.
On négligera toutes les actions dues à l’air ainsi que la perte de
masse de la fusée pendant qu’elle brille et on considèrera cette
dernière comme un objet ponctuel.
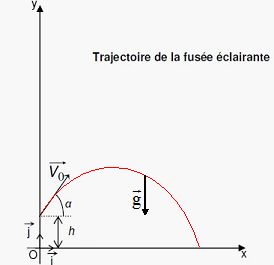
On définit un repère (O,i ,j) avec O au niveau du sol et tel que la
position initiale de la fusée éclairante à la sortie du pistolet soit à
une hauteur h = 1,8 m. Le vecteur vitesse initiale v0 est
dans le plan (O,x,y) ; Ox est horizontal et Oy est vertical et orienté
vers le haut.
À l’instant t = 0 s, le vecteur vitesse de la fusée éclairante fait un
angle α égal à 55 ° avec
l’axe Ox et sa valeur est v0 = 50 m.s−1.
Représenter le
vecteur champ de pesanteur g sur le schéma donné et tracer
qualitativement l’allure de la trajectoire suivie par la fusée
éclairante dans ce champ de pesanteur.
En
utilisant une loi de Newton que l’on énoncera, déterminer les
coordonnées du vecteur accélération de la fusée éclairante : ax(t) suivant x et ay(t) suivant y.
Dans un référentiel galiléen, la somme vectorielle des forces
appliquées au système est égale au produit de la masse du système par
le vecteur accélération du centre d'inertie du système.
La fusée est soumise uniquement à son poids, vertical, orienté vers le
bas, valeur mfg. En conséquence ax(t) = 0 et ay(t)
= -g.
En
déduire les expressions des coordonnées vx(t) et vy(t) du vecteur
vitesse de la fusée éclairante et montrer que les équations horaires du
mouvement de la fusée s’écrivent x(t) = v0.cos(α).t et y(t) =-½gt2 + v0.sin(α).t +h.
La vitesse est une primitive de l'accélération : vx(t) = ax(t)
+ constante et vy(t)
= ay(t) + autre constante.
Les constantes sont déterminées par la vitesse à l'instant t=0.
vx(0)
= 0 + constante =v0.cos(α).
vy(0
= -g*0 + autre constante = v0.sin(α).
vx(t)
=v0.cos(α) et vy(t)
= -gt +v0.sin(α).
La position est une primitive de la vitesse.
x(t) = v0.cos(α) t + constante ; y(t) = -½gt2
+v0.sin(α) t + autre constante.
Les
constantes sont déterminées par la position à l'instant t=0.
x(0) = 0 +constante = 0 ; y(0) = h = autre
constante.
x(t)
= v0.cos(α).t et
y(t) =-½gt2 + v0.sin(α).t +h.
Déterminer la valeur
de la durée du vol de la fusée éclairante.
Résoudre y(t)
=-½gt2 + v0.sin(α).t +h = 0.
-4,9 t2 +50*sin 55 t + 1,8 = 0 ; t2-8,36 t
-0,367=0.
D =8,362+4*0,367
=71,36 ; D½ =
8,447.
t =(8,36 + 8,447)/2 = 8,4 s ; l'autre valeur est négative : elle ne
peut pas convenir.
|
| .
. |
|
|
Calculer l’altitude
à partir de laquelle la fusée commence à éclairer puis l’altitude à
laquelle elle s’arrête.
Ces valeurs paraissent-elles adaptées au but recherché ?
Une
fusée éclairante s’allume 1,0 seconde après son départ du
pistolet et éclaire d’une façon intense pendant 6 secondes environ.
y(t=1) = -4,9 +50*sin
55 + 1,8 =37,86 ~38 m.
y(t=7) =-4,9 *72 + 50*sin
55 *7+ 1,8 ~ 48 m.
Ces valeurs sont adaptées au but recherché : le champ de bataille est
éclairé et la fusée est vue d'assez loin.
|
.
|
|
Pour aller un peu plus loin.
Par souci de simplification, on ne considère que le système {pistolet −
fusée} et on s’intéresse à sa quantité de mouvement. La masse du
pistolet à vide est mp = 0,98 kg.
Exprimer
la quantité de mouvement totale p du système
{pistolet − fusée} avant que la fusée ne quitte le pistolet puis
montrer que celle-ci est équivalente au vecteur nul.
Éjection de la fusée
Que
peut-on dire de la quantité de mouvement totale du système {pistolet −
fusée}si l’on considère ce système comme un système isolé au cours de
l’éjection de la fusée du pistolet ?
Le vecteur quantité de mouvement d'un système isolé se
conserve.
En
déduire dans ce cas l’expression vectorielle de la vitesse vp de recul du
pistolet juste après l’éjection de la fusée en fonction de la masse du
pistolet mp, de la masse de la
fusée mf et du
vecteur
vitesse initiale de la fusée v0.
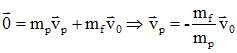
Le signe moins traduit le recul du pistolet ; vp = 0,058 *50
/ 0,98 ~3,0 m/s.
La valeur réelle de la vitesse est beaucoup plus faible que la
valeur que l’on obtient à la question précédente. Pourquoi
observe-t-on une telle différence ? Justifier la réponse.
La masse de la fusée n'est pas constante, elle diminue au fur et à
mesure que le combustible est consommé.
|
|