Laser et stockage optique. Bac S Nlle Calédonie  2013 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Lecture d'un disque optique. Les diodes lasers utilisées dans les lecteurs blu-ray émettent une lumière de longueur d'onde l = 405 nm. Calculer l'énergie d'un photon associé à cette radiation. E = h c / l = 6,63 10-34 *3,00 108 / (405 10-9) =4,91 10-19 J. Indiquer les processus d'émission d'une DEL et d'un laser et indiquer au moins deux caractéristiques de la lumière émise par un laser. En appliquant une tension électrique  dans une zone de jonction de semi-conducteurs, on observe l'émission de lumière. Pour la DEL, il s'agit d'émission spontanée. Pour la diode laser l'émission stimulée est prépondérante. La lumière laser est quasiment monochromatique, le faisceau est très directif et la puissance transportée par unité de surface est très grande. On admet que la profondeur d'une cuvette est égale à l/4, où l est la longueur d'onde du faisceau laser utilisé. Pour chacun des cas a) ou b) du document suivant, calculer la distance supplémentaire d parcourue par le rayon (2) par rapport au rayon (1). 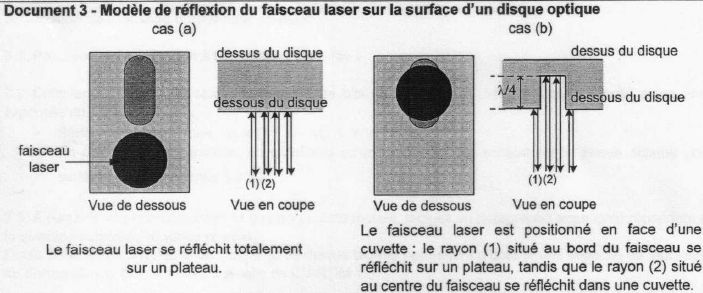a) les faisceaux 1 et 2 parcourent la même distance d=0. b) le faisceau 2 parcourt un plus gande distance que le faisceau 1 : d = ½l.( deux fois la profondeur d'une cuvette). Le dispositif optique précédent permet aux rayons (1) et (2) d'interférer après réflexion sur le disque optique. Comparer l'intensité lumineuse du faisceau réfléchi sur un plateau avec celle du faisceau réfléchi dans une cuvette. La différence de marche d est nulle dans le cas d'une réflexion sur un plateau. Les interférences sont constructives et l'intensité lumineuse est maximale. La différence de marche d est un multiple impaire de la demi-longueur d'onde dans le cas d'une réflexion sur une cuvette. Les interférences sont destructives et l'intensité lumineuse est minimale. Comment les variations d'intensité lumineuse sont-elles associées aux bits ? ( de valeur 0 ou 1). Un bit "1" est associé au passage d'un plat à un creux, c'est à dire quand l'intensité lumineuse reçue par le capteur varie. Un bit "0" est associé à une intensité lumineuse consatnte ( maximale ou minimale). . . Traitement de l'information numérique. Un son est enregistré sous forme d'échantillons à 44,1 kHz avec 16 bits par canal. Sachant qu'il y a deux canaux de son stéréophonique, le débit binaire est donc de 176 ko s-1. Le CD-ROM de capacité 780 Mo, peut contenir 74 minutes de son. Justifier la fréquence d'échantillonnage utilisée pour numériser le son. Echantillonner un signal consiste à capturer des valeurs à intervalles réguliers puis à transmettre celles-ci. L'échantillonnage produit une suite de valeurs discrètes. Le domaine de fréquences audibles par l'homme est limité à 20 kHz. La fréquence d'échantillonnage doit être égale ou supérieure au double de la fréquence maximale contenue dans ce signal, afin de le numériser correctement. On suppose que le convertisseur analogique-numérique utilisé pour l'échantillonnage fonctionne avec une tension maximale Umax = 10 V. Calculer son pas de tension. Le pas "p" en tension d'un CAN est le plus petit écart de tension entre deux points du signal numérisé. Il est relié au nombre de bits n et à la tension maximale Umax du convertisseur par : p =Umax / (2n-1). p = 10 / (216-1)=1,53 10-4 V. A partir de la valeur de la fréquence d'échantillonnage, rerouver par le calcul la valeur du débit binaire. Fréquence d'échantillonnage fois le nombre d'octets =44,1 *4 = 176 ko s-1. Retrouver la capacité de stockage exprimée en Mo d'un CD-ROM audio pouvant contenir 74 minutes de son. Période de l'échantillonnage : 1 / (44,1 103) = 2,268 10-5 s. Nombre de valeurs obtenues en 74 minutes : 74*60 / (2,268 10-5) =1,958 108. Chaque valeur est codée sur 2*16 bits soit 4 octets. Nombre d'octets : 4*1,958 108 =7,83 108 soit 783 Mo. ou bien : 176 103 *60*74 =7,81 108 octets ou 781 Mo. Si on enregistrait un signal purement audio de même débit binaire sur un disque blu-ray affichant une capacité de 22 Go, quelle serait la durée de lecture en heures ? 22 103*74 /780 =2087 min ou  environ 35 heures. . Capacité de stockage d'un disque optique. Proposer une justification de l'appellation blu-ray. La longueur d'onde du faisceau appartient à la teinte violette du domaine visible. 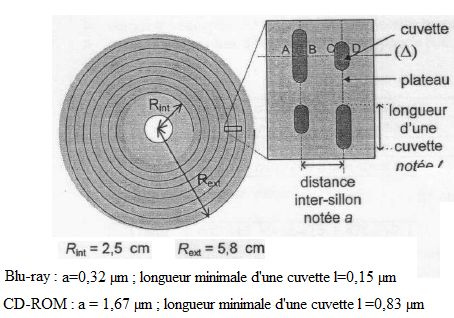Calculer la capacité de stockage ( nombre de bits stockés) d'un CD-ROM. Surface de la couronne : S =(R2ext-R2int) p =((5,8 10-2)2 -(2,5 10-2)2 )*3,14 =8,605 10-3 m2.S urface effective occupée par un bit de donnée : s = l a =1,67 10-6 *0,83 10-6 =1,386 10-12 m2. Capacité de stockage : 8,605 10-3 / (1,386 10-12)= 6,21 109 bits ou 6,21 103 mégabits ou 6,21 103 /8=776 Mo. Quels paramètres physiques du lecteur et du disque blu-ray permettent d'obtenir une capacité de stockage du disque blu-ray bien supérieure à celle du CD-ROM ? La taille du point sur lequel le laser peut être focalisé est limitée par la diffraction. 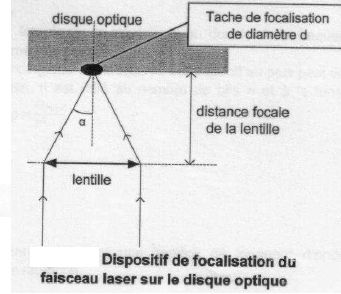Le laser doit être focalisé avec une grande précision sur la surface du disque. Diamètre du spot sur le disque : d =1,22 l / sin a. En diminuant la longueur d'onde du faisceau laser, en utilisant une meilleur ouverture numérique de la lentille ( système à double lentilles ), on diminue la taille du spot, ce qui permet de stocker d'avantage de données. Ajoutons qu'un disque plus fin diminue certains effets d'optiques. On améliore aussi l'encodage des données et on rapproche les pistes entre-elles.

menu