Teneur en cuivre d'une pièce de 5
centimes d'euro.
Bac S
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
La pièce de 5
centimes d’euro est composée d'un centre en acier (constitué
essentiellement de fer et de carbone) entouré de cuivre. Elle a un
diamètre de 21,25 mm, une épaisseur de 1,67 mm et une masse de 3,93 g.
On cherche par une méthode spectrophotométrique à déterminer la teneur
en cuivre d’une telle pièce.
Le cuivre, de masse molaire 63,5 g.mol-1, est un métal qui
peut être totalement oxydé en ions cuivre (II) par un oxydant puissant
tel que l’acide nitrique selon la réaction d’équation :
3 Cu(s) + 8 H+(aq) + 2 NO3-(aq) ---> 3 Cu2+(aq) + 4 H2O(l) + 2 NO(g)
Les ions cuivre (II) formés se retrouvent intégralement dissous en
solution ; le monoxyde d’azote NO est un gaz peu soluble. En pratique,
on dépose une pièce de 5 centimes dans un erlenmeyer de 100 mL, on
place cet erlenmeyer sous la hotte et on met en fonctionnement la
ventilation. Équipé de gants et de lunettes de protection, on verse
dans l’erlenmeyer 20 mL d’une solution d’acide nitrique d’une
concentration environ égale à 7 mol.L-1.
La pièce est alors assez vite oxydée et on obtient une solution notée S1. On transfère intégralement cette solution S1
dans une fiole jaugée de 100 mL et on complète cette dernière avec de
l’eau distillée jusqu’au trait de jauge. On obtient une solution S2 qui contient autant d’ions cuivre (II) qu’il y avait d’atomes de cuivre dans la pièce de départ. La solution S2
contient également des ions fer (III) provenant de la réaction entre
l’acide nitrique et le fer contenu dans le centre en acier de la pièce.
L’absorbance de la solution S2 à 800 nm est mesurée, elle vaut 0,575.
Déterminer, en argumentant
votre réponse, les couleurs attendues pour une solution d’ions cuivre
(II) et pour une solution d’ions fer (III). Pour quelle raison
choisit-on de travailler à une longueur d’onde de 800 nm ?
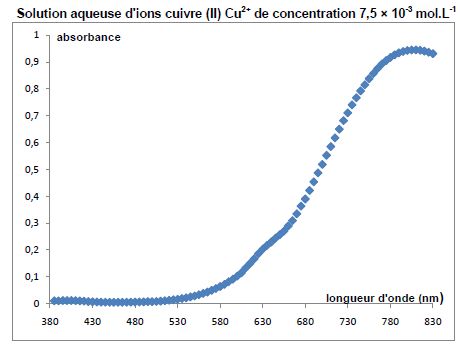
La solution d'ion cuivre II présente un maximum d'absorbtion vers 800
nm : le rouge est donc absorbé ; la solution d'ion cuivre II a la
couleur complémentaire du rouge, c'est à dire le bleu vert. Pour une
meilleur précision, on travaille à une longueur d'onde pour laquelle
l'absorption est maximale.
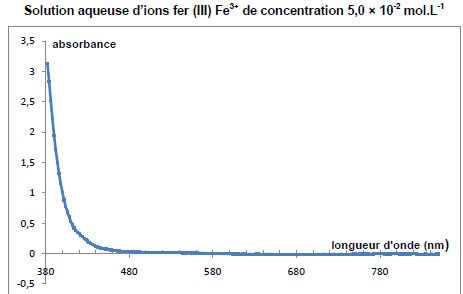
La
solution d'ion fer III présente un maximum d'absorbtion vers 380 nm :
le violet est donc absorbé ; la solution d'ion fer III a la couleur
complémentaire du violet, c'est à dire le jaune vert.
|
.
.
|
|
|
On fait subir à différents échantillons de métal cuivre pur le
même traitement que celui décrit ci-dessus pour la pièce. On obtient
alors des solutions d’ions cuivre (II) dont on mesure l’absorbance à
800 nm.
Montrer que la loi de Beer-Lambert est vérifiée
pour ces solutions d’ions cuivre (II).
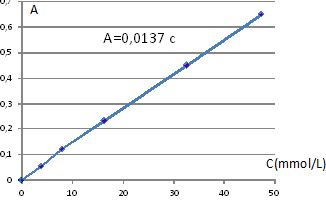
Le graphe A = f(c) est une droite passant par l'origine. Absorbance et
concentration sont proportionnelles : la loi de Beer est bien vérifiée.
Déterminer la masse de cuivre contenue dans la pièce de 5 centimes d’euro.

L’absorbance de la solution S2 à 800 nm est mesurée, elle vaut 0,575.
m = 0,575 / 0,0216 =266 mg.
En déduire la teneur (ou « pourcentage massique ») en cuivre dans la pièce.
100 * masse de cuivre / masse de la pièce = 100 *0,266 / 3,93 =6,77 ~6,8 %.
|
.
|
|
Incertitude.
10 groupes d’élèves ont déterminé expérimentalement la masse de cuivre
présente dans 10 pièces de 5 centimes de même masse. Leurs résultats
sont les suivants :
Groupe
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
Masse de cuivre (mg)
|
260
|
270
|
265
|
263
|
264
|
265
|
262
|
261
|
269
|
267
|
Déterminer, grâce aux valeurs trouvées par les élèves, l’incertitude
élargie (pour un niveau de confiance de 95 %) sur la mesure de la masse
de cuivre dans une pièce.
Ecart type s = 3,30 ; incertitude type sur la moyenne : u= s / n½ = 3,30 / 10½ =1,046 ;
incertitude élargie : U =2 u = 2,1.
En
déduire l’intervalle dans lequel devrait se situer le résultat du
mesurage de la masse de cuivre avec un niveau de confiance de 95 %.
Moyenne : 264,6 ~265 mg ; intervalle : 265 -2 ; 265+2 soit 263 mg ; 267 mg.
|
|
|



