CD et autres
supports de l'information. Bac S Antilles 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Sur
un Compact-disc, les informations sont stockées sous forme de "creux"
et de "plats" le long d'une piste métallique réfléchissante en forme de
spirale. Celle-ci démarre à une distance R 1 = 2,50 cm de l'axe du CD, et se termine à R 2 = 5,8 cm.
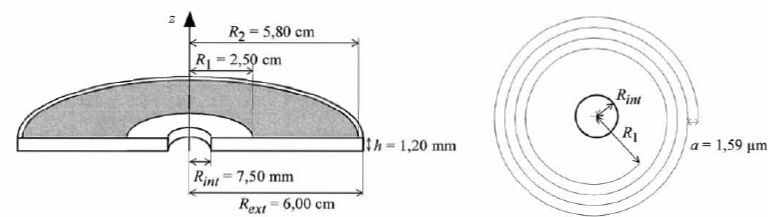
La zone grisée correspond à la portion du CD occupée par la piste
métallique, la partie blanche est le substrat en polycarbonate. Les
spécifications du CD recommandent une vitesse de lecture linéaire v 0 = 1,22 m/s et un pas de spirale a = 1,59 µm. On peut noter que a << R 1.
Etablir
l'expression littérale de la "surface utile " S du CD, c'est à dire la
surface grisée sur laquelle s'étend la piste en spirale.
S = p R22 - p R12 = p(R22-R12).
Donner
sans démonstration, une estimation de la longueur totale L de la piste
en fonction de S et a. Calculer sa valeur numérique.
L~S / a ~ p(R22-R12) / a = 3,14 ( 5,802-2,502 )10-4 / 1,59 10-6 =5411,8 ~5,41 103 m ~5,4 km.
Quelle valeur numérique de la durée de lecture Dt exprimée en minutes, cela représente t-il ?
Dt = L/ v0 = 5411,8 / 1,22 = 4436 s = 73,9 min ~74 min.
Lorsque
le spot laser se réfléchit autour d'une alvéole, il y a interférences
entre la partie de l'onde qui se réfléchit sur la plat et celle qui se
réfléchit sur le creux.
Déterminer la différence de parcours entre ces deux ondes.
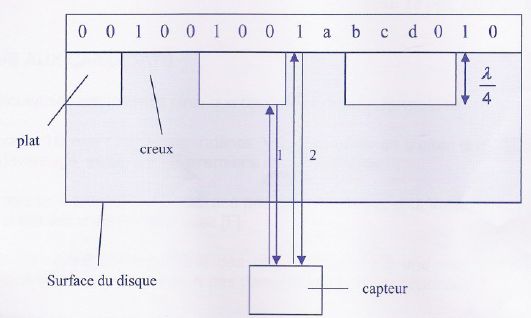 La
différence de parcours est égale à deux fois la hauteur d'un creux,
c'est à dire à la moitié de la longueur d'onde de la lumière
laser dans le polycarbonate soit ½l= 0,5 *503 =252 nm.
La
différence de parcours est égale à deux fois la hauteur d'un creux,
c'est à dire à la moitié de la longueur d'onde de la lumière
laser dans le polycarbonate soit ½l= 0,5 *503 =252 nm.
Déterminer le retard de l'onde réfléchie dans un creux par rapport à l'onde réfléchie sur un plat au niveau du capteur.
Retard t = 2hc / v =l /(2v)=vT /(2v) = ½T = 0,5 *503 10-9 / (1,93 108) =1,3 10-15 s.
La partie du faisceau laser réfléchie au niveau
d'un plat (1) et celle réfléchie au niveau d'un creux (2) arrivent au
capteur avec un déphasage d'une demi-période ou p radian.
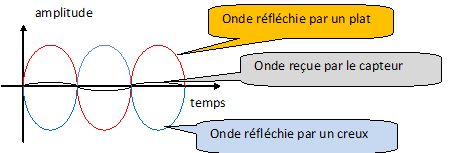
En déduire le type d'interférences.
Si les
radiations lumineuses, qui interfèrent en un point M donné, sont en
opposition de phase, l'intensité lumineuse en M est minimale. Les interférences sont destructives.
|
| .
. |
|
|
Déterminer la capacité totale théorique d'information ( en Mo) que l'on peut enregistrer sur ce CD.
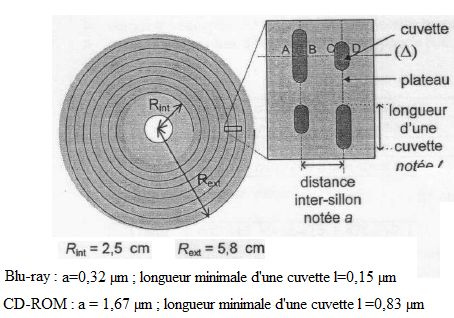
Calculer la capacité totale théorique de stockage ( nombre de bits stockés) d'un CD-ROM.
La taille d'un bit correspond à la distance parcourue par le faisceau
lumineux en 231,4 ns avec une vitesse de lecture linéaire de 1,2 m/s
soit : 231,4 10-9 *1,2 =2,78 10-7 m.
Capacité de stockage : longueur de la spirale / taille d'un bit =5,4 103 / (2,78 10-7)~ 1,9 1010 bits.
Il faut 17 bits sur le CD pour stocker un octet.
1,9 1010 / 17 = 1,1 109 octets ou 1,1 103 Mo.
|
.
|
|
La technologie blu-ray fut développée au début des années 2000. Le principe de fonctionnement est le même que celui d'un CD.
Quelle doit être la profondeur d'un creux sur un disque Blu-ray ?
La profondeur d'un creux est liée à la longueur d'onde du laser dans le polycarbonate: hc= 0,25 l = 0,25 *261 = 65,3 nm.
Pouquoi ne peut-on pas lire un disque blu-ray avec un lecteur CD ?
La largeur du faisceau laser et la profondeur des cuvettes sont différentes.
On suppose que le codage de l'information et la lecture d'un disque Blu-ray sont identiques à ceux d'un CD.
Déterminer la capacité de stockage d'un disque Blu-ray et conclure.
La longueur de la piste est de 27 km au lieu de 5,4 km. Dans l'hypothèse où la taille d'un bit reste identique :
on peut donc stocker 27/5,4 = 5 fois plus de données que sur un CD.
Cette valeur est très inférieure à la capacité annoncée, 25 Go : le
codage de l'information sur le Blu-ray diffère du standard EFM.
|
|
|