Un trou noir au
centre de la galaxie. Bac S Antilles 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Enoncer la première loi de kepler et expliquer comment la trajectoire de l'étoile S2 a permis de justifier l'existence d'un trou noir très massif au centre de la galaxie.
Première loi ou loi des orbites :
dans le référentiel lié au centre de la galaxie, l'orbite de chaque
étoile est une ellipse dont l'un des foyers est le centre de la galaxie.
La trajectoire de l'étoile S2 suit la première loi de Kepler
; le centre de la galaxie, foyer de l'ellipse, est donc très massif.
Seul un trou noir peut avoir une telle masse.
Pour quelle raison doit-on utiliser l'optique adaptative pour mettre en évidence la présence de ce trou noir ?
L'optique
adaptative permet de corriger en temps réel les déformations de l'image
obtenue par un instrument d'optique, déformations provoquées par les
turbulences atmosphériques.
Expliquer pourquoi une étoile guide laser peut être nécessaire pour utiliser l'optique adaptative avec un télescope.
Une
étoile très brillante doit servir de référence dans le champ de l'objet
observé. Or ce type d'étoile ne se trouve pas toujours dans le
champ d'observation. On a donc recourt à une étoile brillante
artificielle installée sur Yepun.
Justifier le choix d'une source laser pour créer une étoile guide.
Le faisceau laser est très directif ; il transporte une grande énergie
par unité de surface. La lumière laser est pratiquement monochromatique.
Comment doit être choisie la longueur d'onde du laser ? Justifier.
La
lumière laser doit exciter les atomes de sodium de la mésosphère afin
de créer une source de lumière artificielle. La longueur d'onde du
laser doit être identique à celle de la lumière émise par la transition
entre deux niveaux d'énergie du sodium.
Interpréter
la création de l'étoile guide à l'aide d'un diagramme de niveaux
d'énergie. Quelle information quantitative cette expérience nous
permet-elle d'avoir sur ces niveaux d'énergie ? 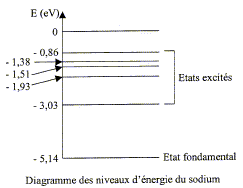
Les niveaux d'énergie d'un atome sont quantifiés. En utilisant le diagramme simplifié des niveaux
d'énergie de l'atome de sodium, on trouve que
l'écart énergétique entre le niveau
excité n=1 et le fondamental vaut : -3,04+5,14 = 2,11
eV ; cette radiation jaune correspond donc à la
transition de l'état excité 1 vers
l'état fondamental.
|
| .
. |
|
|
Pour déterminer un ordre de grandeur de la masse M du trou noir, on considère que l'étoile S2, de masse m, décrit une orbite circulaire de rayon r = 132 heures-lumière, la période de révolution étant T = 15,2 ans.
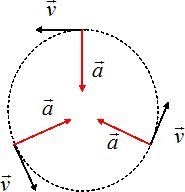
Schématiser
la trajectoire de cette étoile et représenter, en plusieurs points de
la trajectoire, son vecteur vitesse, son vecteur accélération.
Le mouvement est circulaire uniforme et l'accélération est centripète.
|
.
|
|
Montrer que la valeur de la vitesse v de l'étoile S2 a pour expression v = (GM/r)½.

En déduire la période T de révolution de l'étoile.
L'étoile d'écrit la circonférence 2pr à la vitesse v en une durée T.
2pr = vT ; T = 2pr / v = 2pr3/2 / (GM)½.
Déterminer la valeur de la masse M du trou noir.
M =4p2r3 /(GT2) ; r = 132*3600*3,00 108 =1,4256 1014 m ; T = 15,2 *365*24*3600=4,793 108 s.
M = 4*3,142*(1,4256 1014)3 /(6,67 10-11*(4,793 108)2) =7,46 1036 kg.
Le texte indique que la masse du trou noir est égale à 3 ou 4 millions de fois la masse du soleil soit environ :
3,5 106 *2,00 1030 = 7 1036 kg, en accord avec le résultat précédent.
|
|
|


