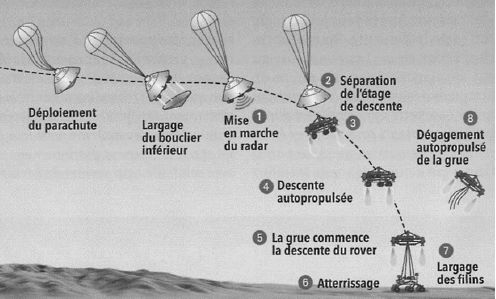
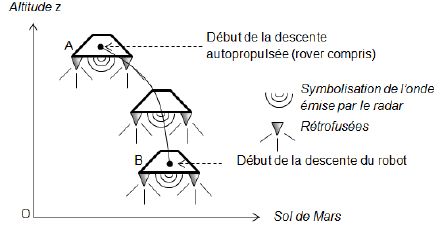
La nouvelle façon de se poser sur Mars. Bac S Afrique 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Les principales étapes de l'atterrissage sur Mars. D'après la recherche n° 471 janvier 2013. La descente autopropulsée. On admet que la masse m de l'étage de descente ( rover compris) est à peu près constante lors de la descente et vaut environ 2,0 103 kg et que le champ de pesanteur martien  est uniforme durant cette phase. Etablir l'expression du travail du poids de l'étage de descente lors de son déplacement du point A à B. 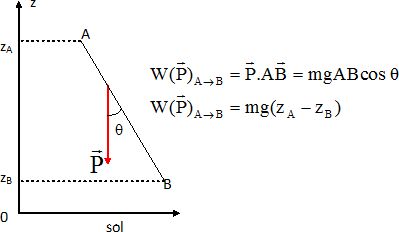A.N : g = 3,7 m s-2 ; zA = 2,0 103 m ; zB = 20 m. L travail du poids est moteur en descente : W = 2,0 103 *3,7 (2,0 103-20) =1,465 107 ~1,5 107 J. . . Evolution de l'énergie mécanique de l'étage de descente. Déterminer l'énergie mécanique en A et en B. vA = 100 m/s ; vB =0,75 m/s. L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. EM(A) = mgzA+½mv2A= 2,0 103(3,7*2,0 103 +0,5 *104)=2,48 107 ~2,5 107 J. EM(B) = mgzB+½mv2B =2,0 103(3,7*20 +0,5 *0,752)=1,48 105 ~1,5 105 J. L'énergie mécanique diminue de la valeur du travail des forces exercées par les rétrofusées. Les forces de frottement sur l'atmosphère ténue  et la poussée d'Archimède sont négligeables. . Estimer la durée Dt de la phase de descente du robot entre le moment où la grue commence à le descendre et son atterrissage martien. A 20 m du sol, l'étage de descente a une vitesse de 0,75 m/s. Il commence alors la descente du robot au bout de trois filins de 7,50 m. Hauteur du robot : 2,2 m Hypothèse : la vitesse de l'étage de descente est constante, égale à 0,75 m/s.Les filins mesurent 7,50 m lorsque le rover touche le sol : l'étage descend donc de 20-7,5-2,2 = 10,3 m. Dt = distance / vitesse =10,3 / 0,75 ~14 s. Une fois le rover déposé, la poussée des moteurs augmente et propulse verticalement l'étage de descente jusu'à une altitude de 50 m au dessus du sol martien. L'étage s'incline alors d'un angle de 45° et les moteurs se coupent. A partir du moment où les moteurs se coupent, justifier que le mouvement est une chute libre. La poussée d'Archimède et les forces de frottement dans une atmosphère ténue sont quasiment nuls. L'étage n'est soumis qu'à son poids et se trouve donc en chute libre. Déterminer la valeur de la vitesse initiale v0 minimale permettant d'écarte l'étage de descente d'au moins 150 m du rover. 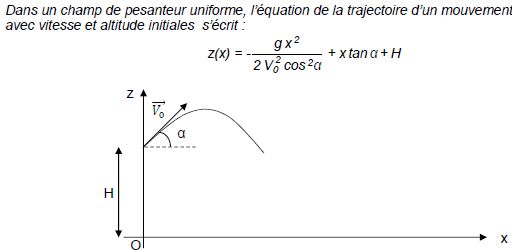0 = -3,7*1502/(2v20 cos245) +150 tan 45 +50. 0 = -8,32 104 /v20 +200 ; v20 =8,32 104 / 200 = 416,25 ; v0 = 20,4 ~20 m/s. .

menu