Rayonnement
fossile de l'univers, ondes, interférences,
concours orthoptie Paris Descartes 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Le rayonnement fossile de l'univers.
Selon
la théorie du big bang, il y a 13,7 milliards d'années, l'univers était
alors extrêmement dense et chaud. Il était constitué de particules qui
ne formaient pas encore les atomes : des protons, des neutrons, des
électrons, des photons.
Les photons étaient en interaction avec les particules chargées : les
photons "rebondissent" sur les électrons et ne peuvent s'éloigner d'eux.
Leur quantité et leurs longueurs d'onde obéisaient aux propriétés du
rayonnement thermique d'un corps dense : la loi de Wien permet de lier
la température d'un corps dense avec la longueur d'onde du rayonnement
qu'il émet : lmax = 2,9 10-3 / T avec T en kelvin et lmax en mètre.
Lorsque l'âge de l'univers a atteint 600 000 an, sa température n'était
plus que de 3000 K et les électrons ont pu se lier aux protons pour
former les premiers atomes. L'univers n'était plus ionisé.
Contrairement aux particules chargées, les atomes neutres laissent
librement voyager les photons. Les physiciens avaient prévu que, selon
la théorie du big bang, les photons devaient remplir l'univers d'un
rayonnement électromagnétique, se propageant dans toutes les
directions. Ce rayonnement n'a pas disparu : il reste un résidu du
rayonnement thermique de l'univers primordial, et devrait devoir une
température très basse, de l'ordre de 5 K, en raison de l'expansion de
l'univers.
En 1965, deux astronomes américains découvrirent un rayonnement
électromagnétique provenant de toutes les directions de l'espace, dont
le maximum d'intensité est celui d'un rayonnement thermique pour une
température de 3 K ( la valeur admise actuellement est 2,73 K). La
communauté scientifique l'identifia comme le rayonnement fossile
attendu.

|
|
|
Comment se trouve la matière au début de la formation de l'univers ?
La
matière est extrêmement dense, constituée de protons, neutrons,
électrons et photons. Les atomes ne sont pas encore formés et les
photons ne sont pas libres.
La lumière peut-elle se propager librement au début de la formation de l'univers ?
La
lumière est constituée de photons : au début de la formation de
l'univers les photons " rebondissent" sur les électrons. La lumière ne
peut donc pas se propager librement dans toutes les directions.
A quelle température les atomes peuvent-ils exister ? Quelle conséquence cela provoque-t-il sur la propagation de la lumière ?
Vers 3000 K les atomes neutres se forment. Ces derniers laissent librement voyager les photons.
Justifier le nom de "rayonnement fossile" que l'on donne souvent au rayonnement primordial.
Le mot "fossile" est lié à très ancien.
Sous quelle forme se présente aujourd'hui le rayonnement le plus ancien que l'on détecte dans l'univers ?
Il s'agit d'un rayonnement électromagnétique.
Quelle est la longueur d'onde du maximum d'émission de ce rayonnement ? A quel type de rayonnement correspond-t-il ?
lmax = 2,9 10-3 / 2,73 = 1,06 10-3 m = 1,06 mm. Ce rayonnement appartient au domaine des ondes radio.
Quelle
était la longueur d'onde du maximum d'émission de ce rayonnement lors
de son émission ? Quel est le type de ce rayonnement ?
lmax = 2,9 10-3 / 3000 = 9,7 10-7 m = 0,97 µm. Ce rayonnement appartient au domaine du proche infrarouge.
Quelle conséquence l'expansion de l'univers a-t-elle sur la lumière émise par les sources très anciennes ou très lointaines ?
On observe un décalage vers les faibles longueurs d'onde.
|
.
|
|
QCM sur les ondes. ( une seule bonne réponse)
Le phénomène suivant n'est pas une onde progressive :
A. la lumière des phares d'une voiture.
B. une bourrasque
de vent. ( phénomène bref et éphémère ne constituant pas la propagation
d'une perturbation, donc ce n'est pas une onde progressive)
C. Le son émis par un piano.
Le phénomène suivant n'est pas une onde sinusoïdale :
A. la voix humaine ( elle est constituée de plusieurs sons ou bruits, ce n'est donc pas ondes sinusoïdale).
B. le son d'un diapason ( c'est un son pur, onde sinusoïdale ).
C. la lumière d'un lase ( elle est quasiment monochromatique ).
La fréquence f d'une onde progressive sinusoïdale de période T =250 ms vaut :
A.1,0 104 s. ( faux f = 1/0,250 = 4,0 Hz). B. 4 s. C. 4 Hz.
Lors d'un orage, on voit l'éclair 30 secondes avant d'entendre le
tonnerre. A quelle distance de l'observateur se produit l'orage ?
A. 1,0 104 m ( 340*30 =1,0 104 m ~10 km). B. 11 m. C. 88 m.
Une onde de fréquence 5 103 Hz et de célérité 5000 m/s a une longueur d'onde de :
A. 5 m ( 5000 / (5 103) = 1 m ). B. 106 m. C. 1 m.
Interférences.
Un groupe d'élèves souhaite étudier le phénomène d'interférences
lumineuses. Ils disposent d'un laser de couleur rouge mais dont ils ne
connaissent pas la longueur d'onde avec précision, de fils calibrés de
diamètre connu, de fentes doubles séparées d'une distance b et de
largeurs d.
Première partie : détermination de la lon,gueur d'onde du laser.
Ils réalisent un montage et recueillent les résultats suivants. La
distance entre le dispositif d'étude ( fils ou fentes ) et l'écran est
D = 3 m.
Largeur de la tache centrale de diffraction L (cm)
|
1,9
|
2,5
|
3,8
|
7,6
|
9,5
|
12,5
|
a(mm)
|
0,2
|
0,15
|
0,1
|
0,05
|
0,04
|
0,03
|
Schématiser le montage réalisé, placer la distance D et les grandeurs a et L. Desiner la figure obersée sur l'écran.
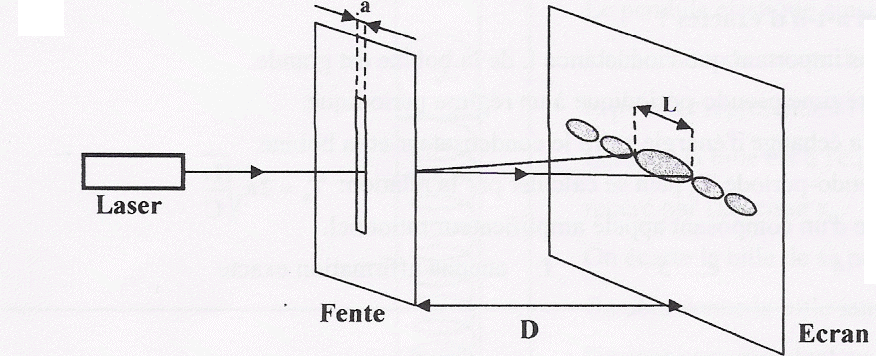 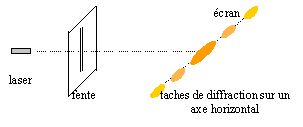
|
Définir le phénomène de diffraction.
Lorsque la lumière rencontre un obstacle ( fil ou fente) dont les
dimensions sont de l'ordre de grandeur de la longueur d'onde, on
observe un éparpillement de la lumière. C'est à dire une tache centrale
brillante, et de part et d'autre une alternance de taches sombres et
brillantes.
Quelle relation existe-t-il entre le diamètre des fils et la longueur d'onde l de la lumière ? Montrer que L = 2lD/a.
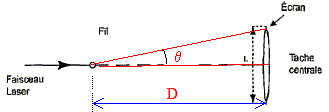
tan q = ½L/D voisin de
q radian pour les angles
petits.
d'autre part q
= l/a.
avec : l longueur d'onde (m)
et a : largeur de la fente (m).
en tenant compte des deux relations ci-dessus :
½L/D=l/a soit
a=2lD/L
ou L = 2l
D/a.
Tracer L en fonction de 1/a. Calculer le coefficient directeur de la droite et en déduire l.
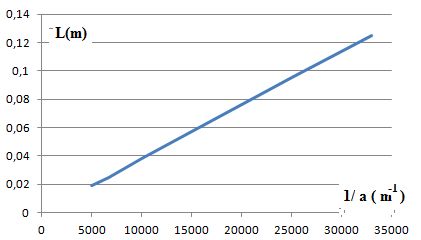
L = 3,79 10-6 / a. On identifie 3,79 10-6 à 2lD d'où l = 3,79 10-6 / 6 =6,32 10-7 m = 0,632 µm.
Deuxième partie : étude des interférences.
En plaçant une fente double à la place des fils, les élèves observent
une figure d'interférences. Ils mesurent les interfranges i.
Décrire la figure l'interférences.
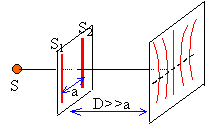
Connaissant l'interfrange i = 1,0 mm, en déduire la valeur de b. On donne i = lD/b.
b = lD/i = 6,32 10-7 *3/(1,0 10-3) =1,9 10-3 m = 1,9 mm.
|
|