Mouvement d'un électron dans un champ électrique uniforme, concours Manipulateur électroradiologie médicale Clermont 2013. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Deux plaques conductrices planes, horizontales A1 et A2, distantes de d sont reliées à un générateur de tension U, la plaque A1 étant reliée au pôle plus. Quelles sont les caractéristiques du champ électrique qui apparaît entre les plaques ? 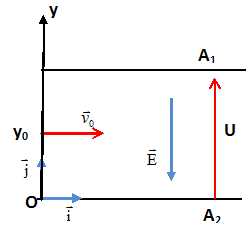Le champ électrique est uniforme, vertical, dirigée vers A2, de valeur E = U/d. Un électron pénètre en B( 0, y0) dans ce champ avec une vitesse horizontale v0. Calculer les valeurs approchées de son poids P et de la force électrique F qui s'exercent sur cet électron. Conclure. Masse de l'électron : m = 9,1 10-31 kg ; charge élémentaire e = 1,6 10-19 C ; g = 9,81 m s-2 ; E = 5000 V m-1. P = mg = 9,1 10-31 *9,81 ~ 9 10-30 N. F = eE = 1,6 10-19 *5000 = 8 10-16 N. Le poids est négligeable devant la force électrique. Etablir, en citant la loi utilisée, l'expression vectorielle de l'accélération de l'électron en fonction de e , m et E. En déduire les expressions littérales des coordonnées de l'accélération. La seconde loi de Newton conduit à : . 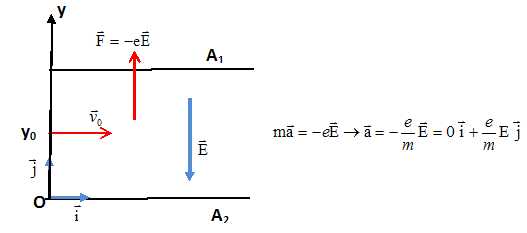En déduire les expressions littérales des coordonnées de la vitesse. La vitesse est une primitive de l'accélération. vx = A ; vy = e/mE t +B avec A et B des constantes. Les conditions initiales v0x=v0 et v0y=0 permettent de déterminer A et B : vx =v0 et vy = e/mE t. En déduire les expressions littérales des coordonnées du vecteur position. La position est une primitive de la vitesse : x = v0 t + C ; y = ½e/mE t2 +D avec C et D des constantes. Les conditions initiales x=0 et y=y0 permettent de déterminer C et D : x = v0 t ; y = ½e/mE t2 +y0. Etablir l'équation de la trajectoire de l'électron. Conclure. t = x/v0, repport dans y : y = ½e/mE (x/v0)2 +y0. Il s'agit d'une branche de parabole. .

menu