La station
spatiale internationale ( ISS) : détermination de la masse d'un
astronaute, concours
Audioprothésiste Rennes 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Par
rapport au référentiel géocentrique, la station ISS effectue 16
révolutions par jour sur une orbite circulaire, inclinée de 21,6 ° par
rapport à l'équateur et située à une altitude h ( environ 40 km ).
Masse de la terre M = 5,97 1024 kg ; rayon de la terre R =
6380 km ; masse de la station m ; G = 6,67 10-11 SI ;
h = 400 km.
Représenter
sur un schéma la force gravitationnelle que la terre exerce sur la
station puis donner son expression vectorielle.
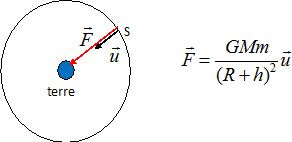
Etude de la
vitesse.
On suppose que seule la force gravitationnelle s'exerce sur la station.
Montrer que le
mouvement est uniforme et établir l'expression de la vitesse en
fonction des données.
La seconde loi de Newton conduit à :
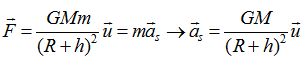
La force de gravitation,
perpendiculaire à la vitesse, ne travaille
pas. En conséquence l'énergie cinétique et la valeur de la vitesse du
satellite ne sont pas modifiées. La valeur de la vitesse étant
constante, le mouvement est uniforme.
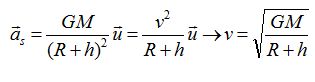
La masse m de la station croît au fur et à mesure de
sa construction.
La
vitesse de la station sur son orbite sera-t-elle modifiée ? Justifier.
La vitesse de la station est indépendante de sa masse. Cette vitesse
restera donc constante.
|
|
|
Définir puis établir
l'expression de la période de révolution de la station en fonction des
données.
La période de
révolution T est la durée nécessaire pour décrire la circonférence 2p(R+h) à la vitesse v constante.
2p(R+h) = v T = (GM / (R+h))½T.
T =2p(R+h)1,5 /
(GM)½.
Satellite
géostationnaire.
Définir un satemmite
géostationnaire.
Un
satellite géostationnaire décrit une orbite circulaire dans le plan
équatorial, à une altitude proche de 36 000 km. Il tourne dans le même
sens que la terre avec la même vitesse angulaire que la terre. Il
paraît fixe pour un observateur terrestre.
La station est-elle
géostationnaire ? Justifier.
Non : son altitude n'est que de 400 km et son orbite est inclinée par
rapport au plan équatorial. De plus il effectue 16 révolution par jour.
|
.
|
|
Détermination de la masse d'un astronaute dans
la satation ISS.
La mesure de la masse est l'un des élément du bilan médical auquel doit
s'attreindre un astronaute. Mais comment se peser dans une navette
spatiale où règne l'apesanteur ? L'utilisation d'un pèse personne
n'étant pas possible, les scientifiques ont utilisé le dispositif de la
chaise oscillante : un siège de masse m0 mobile sur un rail
à coussin d'air est fixé à l'extrémité d'un ressort, l'autre extrémité
étant reliée à un point fixe de l'engin spatial.
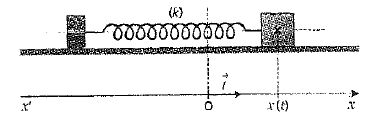
Système solide-ressort à un instant t quelconque.
Ecarté de sa position d'équilibre puis lâché sans vitesse initiale à
t=0 s, le solide (S) oscille avec une période propre T0 = 2p(m/k)½.
On donne m = 100 kg et k = 6,1 102 N /m.
Le choix des états de référence est tel que :
L'énergie potentielle de pesanteur Epp est nulle à
l'altitude du centre d'inertie G et l'énergie potentielle élastique Epe
a pour expression Epe = ½kx2.
Donner l'expression
de l'énergie mécanique Em du système solide-ressort
horizontal à la position d'abscisse x quelconque.
Em = Ecinétique + Epp + Epe
= ½mv2 + ½kx2.
On donne les courbes de l'énergie mécanique, de l'énergie potentielle
élastique et de l'énergie cinétique.
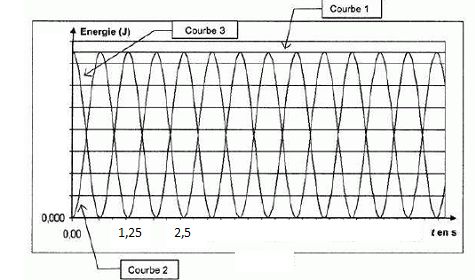
Attribuer à chaque
courbe la forme d'énergie représentée en justifiant. Justifier
l'hypothèse consistant à négliger les frottements.
Courbe 1 :
en absence de frottement l'énergie mécanique est constante.
Courbe 2 :
la vitesse initiale, donc l'énergie cinétique est nulle.
Courbe 3 :
l'énergie mécanique initiale est sous forme potentielle élastique.
Comparer
la période des évolurions de Ec(t) ou de Epe(t)
avec T0. Justifier.
x(t) est de la forme A cos ( 2pt/T0)
avec A une constante.
Epe(t) est proportionnelle à x2 donc à cos2( 2pt/T0).
La période de Epe(t) est donc égale à ½T0.
|
La
période propre T1 des oscillations de la chaise à vide de
masse m0 est égale à 1,28 s.
Lorsque l'astronaute de masse M est arrimé sur la chaise, la période T2
des oscillations est égale à 2,39 s.
Donner
l'expression littérale de T1 et de T2 puis vérifier que
la masse de l'astraunote M vérifie l'expression M =m0(T22/T12-1).
T1 = 2 p (m0/k)½
; T2 = 2 p ((m0+M)/k)½
;
T12
= 2 p (m0/k) ; T22 = 2 p ((m0+M)/k) ;
T22 / T12 = (m0+M)/m0 = 1 +M/m0
; M =m0(T22/T12-1).
Calculer
M si m0 = 25,2 kg.
M = 25,2 ((2,39/1,28)2-1) =62,7 kg.
|
|