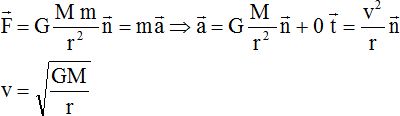|
|
|
|
Document
A. Principe du GPS.
Le
GPS est un système fondé sur la transmission de signaux radio émis par
une trentaine de satellites et de stations au sol. Les satellites
jouent le rôle de points de référence et servent au GPS pour calculer
les coordonnées d'un utilisateur, en fonction des distances qui le
séparent d'au moins trois satellites.
Le principe d'une mesure est le suivant : un utilisateur détermine sa
distance à un premier satellite. Il peut alors affirmer qu'il se trouve
sur la surface d'une sphère de rayon égal à cette distance et centrée
sur ce satellite. L'utilisateur détermine ensuite sa distance à un
deuxième satellite, ce qui lui permet de déduire qu'il se trouve à
l'intersection de deux sphères, c'est à dire sur un cercle.
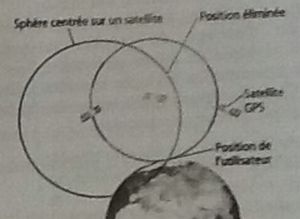
Enfin
, la détermination de sa distance à un troisième satellite place
l'utilisateur sur une troisième sphère, ce qui réduit ses positions
possibles à deux points, l'utilisateur peut soit effectuer une
quatrième mesure, soit rejeter le point dont l'altitude est aberrante.
Pour la science n°320, juin 2004.
Document B
: GPS et incertitude.
Le
GPS permet de repérer un lieu géographique à la surface de la terre
avec une précision de 20 m. Ce dispositif utilise des satellites
émettant toutes les millisecondes des ondes radio de fréquence de
l'ordre de 1,5 GHz, dont la réception au sol permet de calculer la
position du récepteur. Cette précision sur la mesure chute
avec
la vitesse du récepteur si celui-ci est en mouvement.
Célérité des ondes radio dans le vide ou dans l'air c = 3 108
m/s ; 1 GHz = 109 Hz.
Document
C1. GPS et horloge.
Si
on considère n'importe quel phénomène se produisant dans le satellite
en mouvement, sa durée telle qu'elle est mesurée par
l'horloge du
satellite est inférieure à la durée du même phénomène telle que le
mesurent les horloges terrestres au repos. C'et la fameuse dilatation
des temps prévue par la relativité restreinte.
La dilatation des temps est-elle notable pour les satellites GPS ? Ces
satellites ne sont pas sur une orbite géostationnaire et se déplacent à
plus de 20 000 km d'altitude à la vitesse de 3874 m/s. Leurs horloges
retardent, par rapport aux horloges terrestres, de 7,1 µs par jour, ce
qui correspond à une erreur de position de 2 km par jour si elle
n'était pas corrigée. S'y ajoute en outre un effet plus important dû à
la relativité générale. Pour la science n°326, déc 2004.
Document
C2.
Relation entre durées dans différents référentiels.
L'intervalle de
temps propre Dtp
entre deux évenements,mesuré dans le référentiel propre, est lié à
l'intervalle de temps Dtm
entre ces mêmes événements mesuré dans un autre référentiel galiléen,
se déplaçant à la vitesse v par la relation :
Dtm
= Dtp
/ [1-(v/c)2]½. Dans le
cas d'une faible vitesse v devant c le rapport v/c est petit.
L'expression peut s'approximer par : Dtm
= Dtp
[1+0,5(v/c)2]
Document D.
Satellite et gravitation.
La constelleation GPS est constituée de 30 satellites ( y compris des
satellites de réserve ) évoluant dans 6 plans orbitaux différents, ces
plans étant régulièrement répartis autour du globe. Chaque plan
contient le centre O de la terre et présente un angle d'inclinaison
identique de 55° par rapport au plan équatorial. Les satellites
parcourent leurs orbites circulaires situées à 20300 km d'altitude en
11 h 58 min, à la vitesse de 13000 km/h.
Données
terrestres RT =6,36 103
km ; MT = 5,97 1024 kg.
Atmosphère environ 200 km d'épaisseur.
G = 6,67 10-11 SI ; valeur de l'accélération
pour un mouvement
circulaire uniforme en fonction de la vitesse v et du rayon R de la
trajectoire a = v2/R.
|
.
|
GPS
et incertitudes.
Quelle
est la longueur d'onde dans le vide des ondes émises par les satellites
?
l
= c / f = 3,00 108 / (1,5 109) =0,20 m.
Quelle est
la durée t1
mise par le signal pour aller du satellite (S) au récepteur (R) si le
satellite est situé à la verticale de (R) à l'altitude h = 20180 km
?
t1 =2,018 107 / (3,00 108)
= 6,727 10-2 ~6,73 10-2 s.
Pour une mesure unique, l'incertitude sur la distance verticale est Dd= 20 m.
Calculer
l'incertitude Dt
sur la durée de propagation du signal. Comparer t1 et
Dt,
commenter.
Dt
/ t1 = Dd
/ d ; Dt
= t1
Dd
/ d = Dd / c = 20 /
(3,00 108) ~6,7 10-8 s,
valeur très inférieure à t1.
L'horloge atomique du satellite doit être d'une grande précision.
Pour une série de N mesures, les lois de la statistiques montrent que
l'incertitude est divisée par un facteur N½.
Calculer
N pour que l'incertitude Dd
passe de 20 m à 20 cm.
L'incertitude Dd
doit être divisée par 20/0,2 =100 ; On doit donc effectuer N =104
mesures.
Le signal GPS étant émis toutes les
milliseconde, calculer
la durée t2
nécessaire pour effectuer ces N mesures.
t2 =10-3 *104
= 10 s.
Quel
autre paramètre peut influencer la précision sur la position du
révepteur mobile ?
Cette précision sur la
mesure chute avec la vitesse du récepteur si celui-ci est en mouvement.
GPS
et horloges.
En approximant le mouvementcirculaire du satellite à un mouvement
rectiligne uniforme ( valable sur de petiites distances), estimer
l'écart entre la durée mesurée par l'horloge embarquée et la durée
propre de un jpour, mesurée sur terre.
v
=13000 km/h = 13000 /3,6 m/s= 3,6 103 m/s ;
[1-(v/c)2]½= [1-(3,6103/
(3,00 108))2]½
=0,999 999 999 855.
Dtm
= Dtp
/0,999 999 999 855 ; Dtm
=1,000 00 000 145 Dtp.
Dtm
- Dtp
=0,000 00 000 145
jour ou 0,000 00 000
145*24*3600 ~1,3 10-5 s~13 µs.
Autre
méthode ( pour les vitesses faibles devant c ) : Dtm
= Dtp
[1+0,5(v/c)2] = Dtp +0,5(v/c)2Dtp.
Dtm
- Dtp
=0,5(v/c)2Dtp = 0,5
(3611,1 / (3,00 108))2
=7,2 10-11 jour ou 6,3 10-6
s = 6,3 µs.
Est-t-elle
du même ordre de grandeur que la valeur du retard indiquée dans le
texte C1
?
Le texte indique 7,1 µs par jour. Le résultat trouvé est donc du même
ordre de grandeur.
Montrer
que la dérive journalière de 7,1 µs engendre bien une incertitude
d'environ 2 km sur la position du récepteur.
7,1 10-6 *3,00 108 =2,1 103
m.
Pourquoi
est-il nécessaire de prendre en compte les effets relativistes
?
Un GPS qui n'est pas suffisamment précis ( précision 2 km )
ne sert plus à grand chose lors de la circulation en ville, par
exemple, où les carrefours sont nombreux.
Citer
au moins une autre source d'erreurs éventuelles.
Cette précision sur la
mesure chute avec la vitesse du récepteur si celui-ci est en mouvement.
S'y ajoute en outre un effet plus
important dû à
la relativité générale.
|
|
GPS
et gravitation. En vous appuyant sur les informations du
document D.
En précisant
le système étudié et le référentiel choisi, établir
l'expression vectorielle de l'accélération du satellite en fonction de
la masse de l'astre attracteur et du rayon "r" de la trajectoire.
Donner les caractéristiques de ce vecteur accélération.
 |
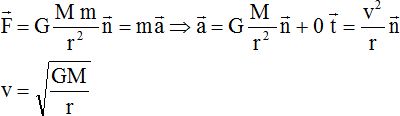 |
Le système
éttudié est le satellite. On se place dans le référentiel géocentrique.
l'accélération est centripète, dirigée vers le centre de la terre ; sa
valeur est GM/r2.
M : masse de la terre ; r : rayon de l'orbite circulaire.
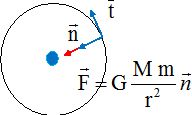
Représenter
sans souci d'échelle dans un plan : la terre, la trajectoire du
satellite, les vecteurs vitesse et accélération, ainsi que la ( les)
force(s) en présence.

Dans
quel référentiel est mesurée la vitesse du satellite ?
La vitese est mesurée dans le référentiel géocentrique.
Montrer
que les données sont compatibles avec la vitesse annoncée à 13 000 km/h.
Les satellites
parcourent leurs orbites circulaires situées à 20300 km d'altitude en
11 h 58 min, à la vitesse de 13000 km/h.
Circonférence : 2p(R+h)
=6,28( 6,36 103 +20300) 103
=1,675 108 m.
Durée du parcours : 11*3600+58*60=4,308 104 s.
Le mouvement étant uniforme :
1,675 108 / (4,308
104)
=3,89 103 m/s ou 3,89 103*3,6
=1,4 104 km/h. Ecart relatif (1,4-1,3) / 1,3
~7,5 %. Les données sont compatibles.
Rappeler
la 3è loi de Kepler.
Pour des satellites en orbite autour d'un astre, le carré de la période
de révolution est proportionnelle au cube du rayon de l'orbite.
T2 = 4 p2
/ (GM) r3.
Montrer
que les données fournies sont compatibles avec la masse de l'astre
attracteur.
M = 4 p2
r3 / (GT2).
T = 4,308
104 s ; r = (
6,36 103 +20300) 103 =
2,67 107 m.
M = 4 *3,142
(2,67
107)3
/ (6,67 10-11 *(4,308
104)2)
=5,94 1024 kg. Les données sont donc compatibles.
|
|