|
|
|
|
Pendule
électrostatique.
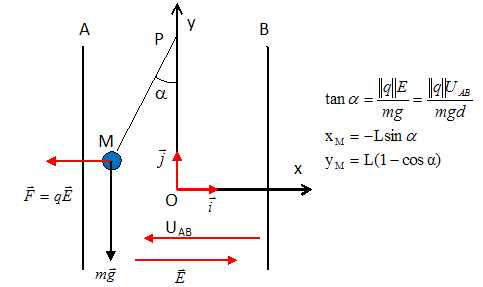
On réalise un pendule électrostatique en reliant une sphère métallique
de masse m, à l'extrémité d'un fil inextensible, de masse négligeable
et de longueur L. l'extrémité supérieure du fil est fixée en un point
P. La sphère métallique, de petite dimension sera considérée comme
ponctuelle et portant la charge q.
On place la shère métallique entre les armatures verticales A et B d'un
condensateur plan non chargé.
la distace des armatures est AB = d. La sphère métallique se trouve
alors en O, situé à égales distances des armatures A et B. On applique
une tension UAB entre les armatures A et B. Il
règne un champ électrostatique entre les armatures.
Le pendule prend une position d'équilibre, en s'écartant de
la verticale d'un angle a
et la sphère se situe en M.
Données : la direction du champ électrostatique est perpendiculaire aux
armatures et le sens de ce champ va de l'armature positive vers
l'armature négative. La valeur du champ est E = |UAB|
/ d.
UAB = 1,0 kV ; q = -15 µC ; L = 25 cm ; d = 12
cm ; m = 27 g ; g = 9,81 m s-2.
Déterminer
les coordonnées xM, yM du
point M ( en cm ). (-10,7 ; 2,4 ) ; (-10,7 ; 3,8 ) ; (0, 0
) ; (10,7 ; 2,4 ) ; (10,7 ; 3,8 ) ; aucune
réponse exacte ).
tan a =
15 10-6 *1000 /(0,027*9,81*0,12)
=0,472 ; a
=25,26°.
xM =-25 sin 25,26 = -10,7
cm ; yM = 25(1-cos25,26) =2,4 cm.
Dipole
électrostatique.
La molécule de chlorure d'hydrogène HCl constitue un dipole
électrostatique. L'atome d'hydrogène porte une charge électrique
partielle ponctuelle positive +
d
et l'atome de chlore une charge électrique partielle ponctuelle -d. Ces deux atomes
sont séparés
par une distance d et la force d'interaction électrique entre eux a
pour valeur 4,4 10-10 N dans le vide. O est le
milieu du
segment joignant les deux atomes.
d
= 2,8 10-20
C ; d = 0,128 nm ; 4,4 / 2,8 =1,6 ; 2,8 / 4,4 = 0,64.
A) Les forces d'interaction électrique entre les deux atomes sont
modélisées par des vecteurs de mêmes normes et de même sens. Faux.
Les forces
sont opposées
: même direction, même norme, sens contraire.
B) Une ligne de champ
électrique reliant
l'atome de chlore, symbolysé par le point N, et l'atome d'hydrogène,
symbolysé par le point P, est orientée de P vers N. Vrai.
C) L'expression littérale de la valeur de la force
d'interaction
électrique entre les deux atomes dans le vide est : F = kd2/d2
avec k
= 9 109 SI. Vrai.
D)
Le vecteur
champ électrique crée par P ou par N au point milieu O est le même.
Vrai.
E ) La valeur du champ électrique créé par le dipole au point O vaut
1,3 1011 V / m environ. Vrai.
Champ créé
par chaque
charge en O : E = kd / (½d)2 =9 109 *2,8
10-20
/ (0,064 10-9)2 =6,1 1010
V/m
Soit pour
les deux
charges, les champs étant égaux ( même direction, sens et norme ) : 1,2
1011 V/m.
|
.
|
Pendule électrostatique.
Soient deux pendules électrostatiques chargés P1 et P2 de formes identiques, tels que : q1 = 1,0 10-9 C et q2 = -q1/9.
Dans une première expérience on observe la position suivante :
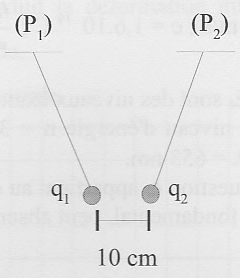
A) La force électrostatique exercée par P1 sur P2 est neuf fois plus intense que celle exercée par P2 sur P1. Faux.
Ces forces ont même valeur.
B) La valeur de F1 de la force électrostatique exercée par P1 sur P2 vaut 1,0 10-7 N. Vrai.
F1 = k q1 |q2| / d2 =9 109 * 1 10-18 / (9*0,12) =1,0 10-7 N.
Dans
une deuxième expérience on provoque le contact entre les deux boules.
On admet la conservation de la charge électrique totale du système, et
on admet que celle-ci se répartit identiquement sur les deux boules. On
observe la nouvelle disposition des pendules :
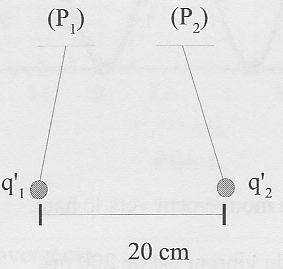
C) Les deux nouvelles charges sont positives. Vrai.
q = ½(q1 + q2 ) =½(1 10-9 - 1 10-9 / 9) =4/9 10-9 = 4,44 10-10 C soit q = 4/9 q1.
D) Les deux nouvelles charges sont négatives. Faux.
E) La nouvelle valeur F2 de la force électrostatique exercée par P1 sur P2 est telle que F2 / F1 = 4/9. Vrai.
F1 = k (1/9) q12 / d2.
F2 = k q q / (2d)2 = k (4/9)2 q12 / (4 d2) =4/9 F1.
|
|