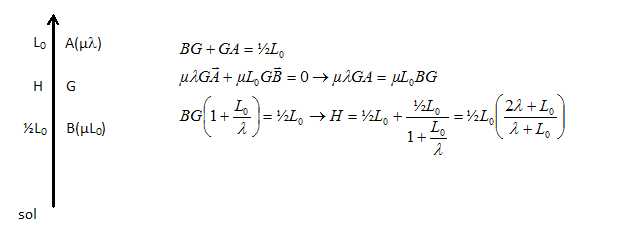|
|
|
|
Le
Jokari est un jeu où l'on frappe une balle en caoutchouc avec une
raquette en bois. La balle est reliée à un socle par un élastique de
masse négligeable. L'élastique ne produit aucun effet lorsque sa
longueur est inférieure à sa longueur à vide L0.
Quand
l'élastique est tendu il se comporte comme un ressort de raideur k,
permettant ainsi à la balle de revenir. Le socle est fixé au sol en un
point O pris comme origine. L'étude du mouvement s'effectue dans le
référentiel terrestre assimilé à un référentiel galiléen. On donne g =
9,80 m s-2.
Mouvement
sans dissipation.
Dans cette partie il n'y a aucun frottement à faire intervenir.
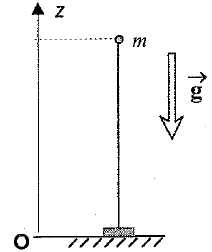
A l'instant initial, on lance la balle avec ue vitesse v0
suivant l'axe Oz ascendant depuis une hauteur h = 1 m ( h <L0).
Quelle
doit être la vitesse minimale vmin au départ
pour que l'élastique se tende ?
L'altitude de la
balle doit être égale à L0 lorsque la vitesse de
la balle s'annule.
Energie mécanique initiale de la balle : ½mv2min
+ mgh.
Energie mécanique finale : mgL0.
Conservation de l'énergie mécanique : ½mv2min
+ mgh = mgL0.
v2min
=2g(L0-h) ; vmin = (2g(L0-h))½.
Dans l'hypothèse où v0 < vmin,
donner
l'expression de lavitesse vz(t) à un
instant t.
La balle est en
chute libre verticale : vz(t) = -gt + v0.
On posera t2
= v02/g2
+2h/g.
En
déduire la fonction z(t). Préciser les expressions de la itesse vs
et de l'instant ts quand la balle touche le sol.
z(t) = -½gt2 + v0t + h.
Au sol, l'énergie mécanique est sous forme cinétique : ½mvs2
;
La conservation de l'énergie mécanique conduit à : ½mvs2
=½mv20
+ mgh.
vs2
= v20
+2gh ; vs2
= g2(v20
/ g2 +2h / g ) = g2
t2
; vs =g t.
vs(t)
= -gts + v0 ; ts
= (v0
- vs(t)
) / g = v0/g - t.
Exprimer
z en fonction de g, v0, vz
et h.
t = ( v0
- vz) / g ; z = -½ ( v0
- vz)2 / g + v0( v0
- vz) / g + h.
z =-½ ( v02
-2v0vz+ vz2)
/ g + (v02
- v0vz)
/ g + h.
z = ½ (v02
- vz2)
/ g + h.
A partir de l'énergie mécanique donner une autre expression de z en
fonction de g, vz et vs.
½mvs2
=½mv2z
+ mgz ; ½vs2
=½v2z
+ gz ; z = ½(vs2
-½v2z
) / g.
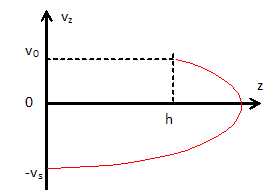
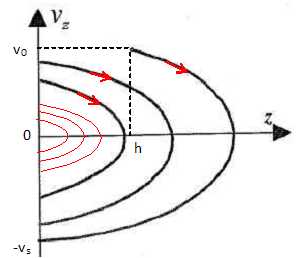
L'espace des phases est un plan où l'on porte en abscisse z et en
ordonnée vz.
Tracer
la courbe correspondante au mouvement de la balle M dans l'espace des
phases pout t appartenant à [0, ts].
Quand la balle touche le sol, on admet que sa vitesse change de sens
instantanément et que l'on peut écrire 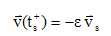 où e est une
constante tel que 0 < e
<1. On pose t' = t-ts. où e est une
constante tel que 0 < e
<1. On pose t' = t-ts.
Quelle
est la nouvelle vitesse vz(t') et la
nouvelle position z(t') ?
vz(t') = -gt' + evs
; z(t') = -½gt'2 + evs t'.
Exprimer
z en fonction de g, vz, e et vs. Comment
pourrait-on mesurer expérimentalement e
?
L'énergie mécanique est sous forme cinétique juste après le rebond : ½m
(-evs)2.
Conservation de l'énergie mécanique : ½m (-evs)2= ½mv2z
+ mgz ; ½ (-evs)2= ½v2z
+ gz.
z = ½((-evs)2-v2z
) / g.
Au point le plus haut vz = 0 : zmax
= ½((-evs)2/ g avec vs
=g t.
La mesure de zmax permet le calcul
de e.
|
On représente
ci-dessous la trajectoire dans l'espace des phases après plusieurs
rebonds.
Compléter
ce graphique. Préciser le sens de parcours.
Pourquoi
a-t-on des tangentes verticales sur l'axe des z ? Par quelle
propriété graphique se traduit la conservation de l'énergie
?
vz = dz/dt ; vz = 0 au
point le plus haut.
Au cours d'un rebond, la trajectoire est symétrique par raport à l'axe
des z.
|
Mouvement
avec dissipation.
La résistance de l'air sur la balle animée d'une vitesse v se traduit
par une force qui en norme vaut f = ßmv2 où
ß est une constante. On lance encore la balle d'une hauteur h
avec une vitesse v0 < vmin,
l'élastique n'étant pas tendu.
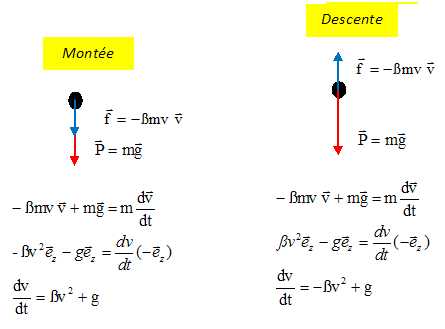
Ecrire
l'équation différentielle vérifiée par v(t) en fonction de g et ßdans
la phase ascendante puis dans la phase descendante.
Montrer
que dans la phase ascendante du/dz = 2g+2ßu. Expliciter
u(z) en fonction de g, ß, v0 et h. En
déduire l'altitude maximale atteinte.
On pose v2 = u ; 2v dv/dt = du/dt ; du/dt
= g(2v) +ßu(2v).
v = dz/dt ; du/dt = 2g dz/dt+2ß u dz/dt ; du/dz = 2 g+2ßu. (1).
Solution générale
de du/dz -2ßu = 0 :
u(z) = A exp(2ßz) ; A est une constante.
Solution particulière de (1) : u(h) =-g/ß.
Solution générale de (1) : u(z) = A exp(2ßz) -g/ß.
u(h) =v20 =A exp(2ßh)-g/ß ; A =(v20 +g/ß)exp(-2ßh).
u(z) =(v20 +g/ß)exp(2ß(z-h))-g/ß.
u(zmax) =0 =(v20 +g/ß) exp(2ß(zmax-h))-g/ß ; 2ß(zmax-h) =ln (g / (ßv20 +g) ; zmax= h +1/(2ß) ln(g / (ßv20 +g).
Expliciter
u(z) dans la phase descendante. En déduire la vitesse vs
quand la balle touche le sol à l'instant ts.
On pose v2
= u ; 2v dv/dt = du/dt ; du/dt = g(2v) +ßu(2v).
v = dz/dt ; du/dt = 2g dz/dt+2ß u dz/dt ; du/dz = 2 g - 2ßu.
(2).
Solution générale
de du/dz +2ßu = 0 :
u(z) = B exp(-2ßz) ; B est une constante.
Solution particulière de (2), régime permanent : u = g / ß.
Solution générale de (2) : u(z) = B exp(-2ßz)
+ g / ß.
u(zmax) = 0 = B exp(-2ßzmax)
+g/ß ; B =-g/ß exp(2ßzmax).
u(z) = -g/ß exp(2ß(zmax-z)+g/ß
= g/ß(1-exp(2ß(zmax-z))). (3).
u(z) = g/ß(1-exp(2ß(zmax-h +h-z))) = g/ß(1-exp(2ß(zmax-h) exp(2ß(h-z))) =g/ß(1-(g / (ßv20 +g)exp(2ß(h-z))).
Au sol z = 0, vz
= vs ; u = vs2 = g/ß(1-(g / (ßv20 +g)exp(2ßh)).
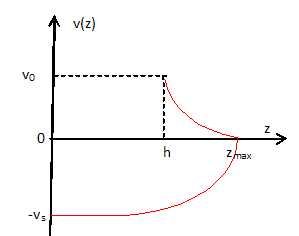
Tracer
l'allure de la trajectoire dans l'espace des phases entre t=0 et ts.
|
Influence
du fil.
Dans cette partie on reprend l'hypothèse de non frottement mais on
considère que le fil possède une masse µL0 ( µ
masse linéïque du fil ) et on écrit la masse de la balle m = l µ.
La balle est lancée verticalement vers le haut depuis le sol avec la
vitesse initiale v0.
Montrer
que si 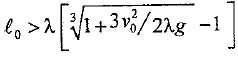 le fil
ne se tend pas. le fil
ne se tend pas.
Le fil ne se tend pas : la balle est à l'altitude L0, le centre de gravité du fil est à l'altitude ½L0 et le barycentre G du système balle + fil est à l'altitude H.
La conservation de l'énergie mécanique donne : v02 = 2g H. Le carré de la vitesse initiale doit être inférieure à 2 gH.
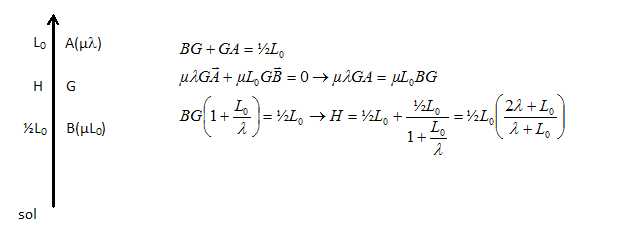
H > v02/(2g) ; ½L0(2l+L0) / (l+L0) > v02/(2g) ; L0(2l+L0) > v02/g (l+L0). On pose X = L0 / l et A =v02/(lg) :
X(2+X) > v02/(lg)(1+X) ; X(2+X) > A(1+X) ; X2 +(2-A)X-A >0.
X étant positif doit être supérieur à la racine positive de cette équation.
D = (2-A)2+4A =(2+A)2 ; D½ = ±(2+A).
X =½ (A-2 +2+A) =A ; L0 / l > v02/(lg).
Etudier le
cas limite µ-->0.
|
|



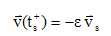 où
où 

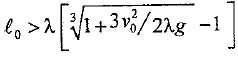 le fil
ne se tend pas
le fil
ne se tend pas