|
|
|
|
Les
diodes laser ont permis de réaliser des instruments capables de
produire un rayonnement ayant toutes les caractéristiques des lasers
traditionnels. Le principal avantage de ces dispositifs réside, outre
leurs faibles dimensions, leurs moindre coûts et leur facilité
d'emploi, dans la possibilité de piloter très simplement la fréquence
d'émission et modifiant l'intensité du courant électrique traversant la
diode. On ne prend pas
en compte l'effet Doppler dans cette question.
Condition
d'accord de phase.
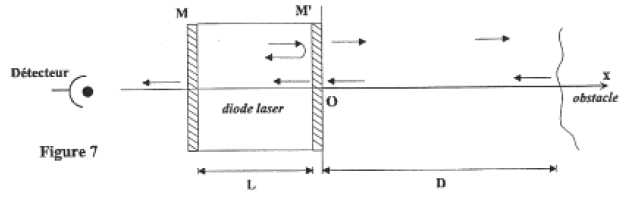
La diode
laser émet une onde lumineuse de pulsation w vers un obstacle
en mouvement rectiligne uniforme de vitesse V suivant un axe Ox.
M
et M' sont des miroirs à haut pouvoir réflecteur. Toutefois, une faible
fraction de l'intensité lumineuse parvient à les traverser. Cette
petite portion de lumière capable de sortir de la diode suffit au bon
fonctionnement de l'expérience.
On note D = D0+Vt, la distance qui sépare
l'obstacle de la diode. L'espace qui sépare l'obstacle de la diode peut
être asimilé à une cavité.
Quand
le rayonnement rétrodiffusé revient, après un aller-retour de longueur
2D entre la diode et l'obstacle, en phase avec l'onde lumineuse émise,
alors la puissance à l'intérieur de la diode augmente et le détecteur
enregistre ce maximum de signal.
On admet que cela se produit
lorsque la distance parcourue par le signal lumineux lors de cet
aller-retour est un multiple de la longueur d'onde du signal. On dit
alors qu'on a réalisé la condition d' accord de phase.
Montrer
que la condition d'accord de phase se traduit par la relation D = p p c / w. (
p entier positif )
On note f la
fréquence : w
= 2 p f ;
f = c/ l
et 2D = p l.
w = 2 p c / l =p p c / D ; D = p p c / w.
Mesure
de vitesse.
Pendant un intervalle de temps Dt
le détecteur enregistre N maxima. En supposant que la vitesse reste
constante pendant le temps de la mesure, montrer que
N = E {VwDt
/( pc) }
où E{ } désigne la fonction partie entière.
D =VDt = p p c / w ; p=VwDt /( pc)
N = E {VwDt /( pc) }.
Pendant Dt = 20 ms avec l = 845 nm, on
détecte 473 372 maxima de puissance. Calculer V.
w = 2 p c / l
; V = N p c /( w Dt) =N l / (2 Dt).
V = 473 372 *845 10-9
/ (2 *0,020) ~10,0 m/s.
Si l'erreur de mesure correspond à une unité de comptage, quelle est
l'incertitude sur la vitesse calculée.
On considère que c et l
sont suffisamment précis.
L'incertitude relative sur la vitesse est égale à l'incertitude
relative sur N soit 1 / 473 372 ~ 2 10-6.
DV
= 10,0 * 2 10-6 ~ 2 10-5
m/s. La mesure de la vitesse est très précise.
|
.
.
Télémétrie.
La technique d'accord de phase est très efficace pour mesurer une
distance.
D
est fixe et on module la fréquence d'émission de la diode laser à
l'aide d'une rampe de courant électrique. L'évolution de la pulsation
lors de la modulation est représenté :
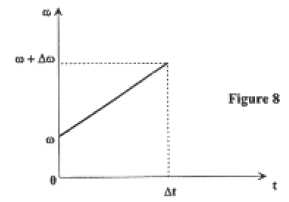
On appelle N' le nombre de maxima enregistré entre 0 et Dt au cours d'une
rampe de modulation. La longueur d'onde associée à la pulsation w est notée l et vaut 845 nm.
Déterminer la relation entre N', Dw, c et D.
D = N' p c / Dw.
Calculer D. N' = 6668 ; Dw = 3,14 1011 rad/s.
D = 6668 *3,14*3,0 108 / (3,14 1011) =20,0 m.
Quelle est est l'incertitude sur la mesure en prenant à nouveau une erreur d'une unité de comptage ?
L'incertitude relative sur la distance est égale à l'incertitude
relative sur N' soit 1 / 6668 ~ 1,5 10-4.
DD
= 20,0 * 1,5 10-4 ~ 3,0 10-3
m.
|
|