Système GPS :
mesure du temps, synchronisation des horloges, dilatation des durées,
Capes 2014.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Mesure du temps.
A l'heure actuelle,
à partir de quel phénomène physique est définie la seconde ? Depuis quelle année
cette définition est-elle en application ?
Depuis 1967, la seconde est la durée de 9 192 631 770 périodes de la radiation
correspondant à la transition entre les niveaux hyperfins F=3 et F=4 de
l’état fondamental 6S ½ de l’atome de césium 133.
La
précision des GPS courants est à l'heure actuelle de l'ordre du mètre.
On suppose que les signaux du GPS se déplacent dans le vide, de façon
rectiligne et à la vitesse c ; en déduire la
précision exigée sur le temps.
On suppose que c = 3,00 108 m/s.
Précision= 1 /(3,00 108) =3,3 10-9 s.
Quel
est l'ordre de grandeur de la précision des horloges atomiques ?
Conviennent-elles pour la mesure des durées dans le système GPS ?
La
précision des horloges atomiques est de l'ordre de 10-15 s.
Elles conviennent pour la mesure des durées dans le système GPS.
Problème
de la synchronisation des horloges.
Pour aborder le problème du positionnement par mesure du temps, on
étudie tout d'abord le repèrage d'un promeneur le long d'une route
étroite.
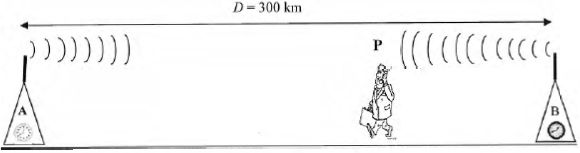
Ce
repérage nécessite deux balises fixes émettrices A et B, situées aux
extrémités de la route de longueur AB=D = 300 km. Le signal émis par
chaque balise contient l'heure d'émission du signal. On suppose ici,
pour simplifier, que la vitesse de propagation du signal est v = 10 km
/min.
Au point P, le promeneur reçoit simultanément un signal de A contenant
l'heure d'émission t0 et un signal de B contenant lui
aussi l'heure à laquelle B a envoyé son signal t0 + Dt ( Dt = 10 min). Les deux balises
sont supposées parfaitement synchronisées.
Donner l'expression
littérale de la distance d1 séparant P de A. Calculer d1.
d 1 = v(t-t 0) ; D-d 1 = v(t-( t0 + Dt)) = d 1-v Dt.
d 1 =½(D+ vDt) =0,5(300+10*10)=200 km.
Lorsque le
promeneur reçoit les deux signaux, sa montre indique tp=10
h24 min. L'heure d'émission des signaux étant connue ( t0 =
10 h 05 min ) on peut déterminer l'avance ou le retard de la montre de
P par rapport aux horloges des balises.
Déterminer l'heure
théorique que devrait indiquer la montre du promeneur lorsqu'il reçoit
les signaux en fonction de D, t0, v et Dt.
d1 =
v(t-t0) ; d2
= v(t-(t0 + Dt))
; d1+d2 = D =v(t-t0) +v(t-(t0
+ Dt)).
D = 2v(t-t0)-vDt ; t-t0 = (D +vDt) / (2v) ; t = t0
+ D/(2v) +½Dt.
En
déduire la valeur numérique du retard t de la montre du
promeneur.
t - t0
= D/(2v) +½Dt = 300 /
20 +0,5 *10 =15 +5 =20 min.
t = 10 h05 +20= 10 h25 min ; t
= tP-t = - 1 min.
La question précédente sous-entend que les horloges A et B sont
synchronisées. Intéressons nous dans un premier temps à la
synchronisation des deux horloges immobiles.
|
|
|
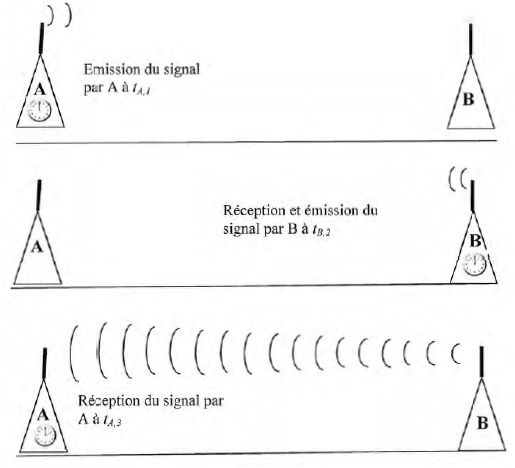
A l'instant tA1 ( selon l'horloge A) l'horloge A émet
un signal lumineux vers l'horloge B. Dès réception, l'horloge B lui
renvoie un signal contenant son heure de réception tB2
( selon l'horloge B) ; l'horloge A reçoit ce second signal à l'instant tA3
( selon A).
A
quelle condition les horloges A et B sont-elles synchronisées ?
D = v(tB2-tA1) ; D = v(tA3-tB2) ; tB2-tA1 =tA3-tB2 ; tB2 = ½(tA3-tA1).
Si tA1 = 10h00 min, tB2 = 10h07 min et tA3
=10h10 min, déterminer
le retard de l'horloge de A sur celle de B.
Si les horloges étaient
synchronisées, tB2 serait égal à : 10h05 min.
A retarde de 2 min par rapport à B.
|
.
|
|
Correction due à la vitesse des satellites : dilatation des durées.
Les horloges atomiques embarquées dans les satellites du GPS sont en
mouvement par rapport à celles situées sur terre. La théorie de la
relativité restreinte permet de montrer que les horloges embarquées
affichent un reatrd par rapport aux horloges terrestres.
En quelle année Einstein a-t-il postulé le principe d'invariance de la vitesse de la lumière ? Enoncer ce principe.
En
1905 : la vitesse de la lumière dans le vide est égale à c dans tous
les référentiels inertiels. Elle ne dépend pas du mouvement de la
source ni de l’observateur.
L'utilisation d'une" horloge de lumière " permet de justifier le
phénomène de dilatation des durées en s'appuyant sur le principe de
l'invariance de la vitesse de la lumière.
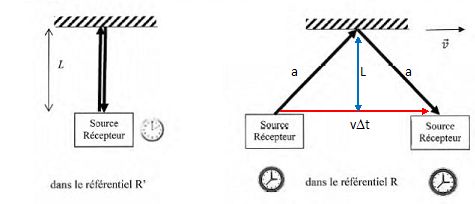
Considérons un ensemble "MSR = miroir ; source; récepteur" en
translation à la vitesse v constante dans le référentiel galiléen du
laboratoire R. On nomme R' le référentiel lié à l'ensemble MSR. Un
observateur lié à l'ensemble MSR détermine l'intervalle de temps Dt'
entre l'émission et la réception d'une impulsion lumineuse, après
réflexion sur le miroir. Pour un observateur lié au référentiel
galiléen du laboratoire R, la durée mise par la lumière pour faire
l'aller-retour est notée Dt.
L désigne la distance fixe entre le miroir et le système source-récepteur.
Définir les notions d'événement et de durée propre.
Un événement est un phénomène
physique localisé, dans un référentiel donné, à la fois dans le temps et dans
l’espace. Un événement est caractérisé par ses coordonnées d'espace et de temps.
Le temps propre d'un
observateur est le temps qui s'écoule dans un référentiel dit "
référentiel propre" dans lequel l'observateur est immobile. Ce temps
propre est mesuré par une horloge fixe placé dans un référentiel
galiléen où se déroule l'événement.
L'intervalle de temps mesuré par deux horloges diférentes situées en
deux lieux différents de l'espace est appelée durée mesurée.
Exprimer la distance parcourue par l'impulsion lumineuse du point de vue des deux observateurs. En éliminant L, en déduire Dt en fonction de Dt', c et v. Justifier le terme de dilatation des durées.
Dans le référentiel R' : Dt' = 2L/c. Dans le référentiel R, l'impulsion parcourt la distance 2a telle que : a2 = L2 +(½vDt)2.
Dt =2a / c = 2 (L2 +(½vDt)2))½ / c =2 ((L/c)2 +(½ v/ c Dt)2))½.
Dt = 2((½Dt' )2 +(½ v/ c Dt)2))½ ; Dt2 =Dt' 2 + v2/ c2 Dt2 ;
Dt 2 (1-v2/ c2)=Dt' 2 ; Dt =Dt' /(1-v2/ c2)½.
Pour un observateur immobile, le temps propre s'écoule plus lentement
dans le référentiel propre en mouvement que dans un référentiel
immobile. Le temps est dilaté.
On suppose que l'on peut appliquer ce résultat pour comparer une durée
propre mesurée par une horloge atomique embarquée dans un satellite à
celle mesurée par un observateur situé dans le référentiel terrestre.
La vitesse du satellite est notée v.
Exprimer le retard t1 de l'horloge embarquée au bout d'une journée T0 = 24 heures mesuré sur terre.
Dt = Dt' /(1-v2/ c2)½ ~ Dt' (1+½v2/ c2)) , v2/ c2 étant petit devant 1.
t1=T0 (Dt-Dt') ~½T0v2/ c2. Dt -Dt' est positif, l'horloge embarquée retarde.
A.N : v = 3,9 km/s.
t1=0,5 *24*3600(3,9 103 / (3,0 108)2 =7,3 10-6 ~7,6 µs.
Doit-on tenir compte de ce retard dans la mise en oeuvre du GPS ?
Au bout d'une journée t1 conduit à une imprécision de 7,3 10-6 *3,0 108 ~2,2 km.
Il faut donc prendre en compte ce retard dans la mise en oeuvre du GPS.
|
Correction due à l'altitude : effet gravitationnel.
Les
satellites se meuvent à l'altitude h de l'ordre de 20000 km. Il s'agit
ici de comparer la période d'une horloge embarquée à celle d'une
horloge restée au sol en prenant en compte uniquement la différence de
potentiel de gravitation ressenti. Cet effet gravitationnel est à
traiter dans le cadre de la relativité générale que nous sllons aborder
ici de façon très simplifiée.
Soit T' la période de l'horloge embarquée mesurée dans le satellite et
T la période d'une horloge identique mesurée sur terre. La correction
gravitationnelle est donnée par : (T-T') / T' = (U-U0)/c2 où U désigne l'énergie potentielle massique de gravitation terrestre au niveau de l'horloge embarquée et U0 celle au niveau de la surface de la terre.
Exprimer U. En déduire l'expression U-U0.
U0 =Ep0 / m = -GM/R avec R : rayon terrestre. L'origine de l'énergie potentielle de gravitation
est prise à l'infini.
U = -GM / (R+h).
U-U0 = GM (1/R -1/(R+h) = GM h / (R(R+h)).
Or g, intensité du champ de gravitation au sol, est égal à : g = GM/R2, d'où : U-U0 =g R h / (R+h).
Comparer T et T' et
justifier l'avance d'une horloge embarquée par rapport à une horloge
restée au sol résultant de la prise en compte de l'effet de gravitation.
(T-T') / T' = (U-U0)/c2 = g R h / ((R+h)c2).
T-T' est positif, T > T', l'horloge embarquée avance par rapport à celle restée au sol en considérant l'effet de gravitation.
Calculer cette avance, notée t2 au bout d'une journée. Commenter.
g R h / ((R+h)c2) = 9,81*6,37 106*2,0 107 / (6,37 106+2,0 107 ) *9,0 1016) =5,27 10-10 s.
t2=T-T' ~24*3600*5,27 10-10 ~ 4,56 10-5 s ~ 45 µs par jour.
Comparer t1 et t2 et conclure.
t2 est environ 7 fois supérieur à t1.
Imprécision au bout d'une journée : (45-7,3) 10-6 *3,0 108 ~11 km
Les satellites sont équipés d'un synthétiseur de fréquence qui permet de corriger les deux effets précédents.
|
|