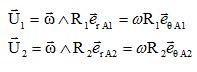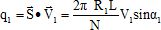|
|
|
|
Le réservoir du haut a une superficie de 6,6 105 m2 et un volume total lorsqu'il est plein de 8,5 millions de m3, le réservoir du bas a un volume total de 9 millions de m3.
L'altitude de la surface libre du réservoir du haut varie entre sa valeur maximale zh max = 406 m et l'altitude minimale zh min
= 395 m. La différence d'altitude entre les surfaces libres du
réservoir du haut et du réservoir du bas est en moyenne égale à H = 225
m. La station possède 4 groupes réversibles turbine- pompe identiques.
Chaque groupe, en mode turbine, développe une puissance de 180 MW et,
en mode pompe, consomme une puissance de 164 MW.
Une STEP est une installation qui fonctionne de façon réversible.
Lorsque le réseau produit un excès d'énergie, elle fonctionne comme une
pompe qui fait remonter l'eau dans le bassin supérieur. Lorsque le
réseau présente une période de surconsommation qui affecte la tension
ou la fréquence délivrée, elle fonctionne comme une turbine qui génère
de l'énergie électrique fournie au réseau.
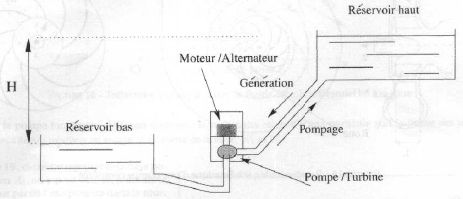
En mode turbine, le débit volumique QT de chaque turbine est 100 m3
/ s. La durée maximale du turbinage en continu est de 5 heures. Avant
le début du turbinage, le réservoir du haut était à son niveau maximum.
Sous quelle forme l'énergie est-elle stockée avant le turbinage ?
Initialement l'énergie est stockée sous forme d'énergie potentielle de pesanteur.
Calculer numériquement la valeur de l'énergie qui a été déstockée pendant les 5 heures de turbinage.
La
masse d'eau qui a quitté le réservoir du haut était à une altitude
moyenne de 225 m au dessus du point qui sert de référence pour
l'énergie stockée.
Masse totale d'eau : m = 4 *100 *103 *3600 *5 =7,2 109 kg.
Variation d'énergie potentielle ( en valeur absolue) :
ESTEP =mgH = 7,2 109 *9,81*225 =1,59 1013 ~1,6 1013 J.
Estimer la puissance moyenne récupérable par chaque turbine.
ESTEP / (4*5*3600) =2,21 108
W =221 MW, valeur un peu supérieure, mais du même ordre de grandeur que
celle donnée dans le texte. La majeure partie de l'énergie potentielle
est convertie en énergie électrique, une faible part est convertie en
chaleur lors des frottements dans les tuyaux.
Considérons un groupe turbo-pompe, notons P0 la puissance
développée par le moteur qui actionne la pompe lorsque le régime
permanent de pompage est établi, et le débit correspondant est Q0.
Soit Hth la hauteur de pompage théorique qui serait obtenue s'il n'y avait aucune perte dans les tuyaux, d'aucune sorte.
Exprimer Hth en fonction de P0, Q0, g et µ0, masse volumique de l'eau.
On considère le système constitué de toute l'eau comprise dans les deux réservoirs et les tuyaux.
P0 = Q0 µ0 g Hth.
Quelle est la relation d'ordre entre Hth et H ?
Hth > H.
Pour interpréter la diffrence entre ces deux hauteurs, on prend en compte l'ensemble des pertes qui peuvent se produire, soit Pp la puissance totale perdue par une pompe.
Etablir le lien entre P0, Pp, H et Hth.
Pp = Q0 µ0 g (Hth -H) = P0 (1-H / Hth).
On définit le rendement de la pompe h = H / Hth.
Calculer h en fonction de P0 et Pp.
Pp =P0 (1-h ) ; h = 1 - Pp / P0.
Calculer Hth et Q0. P0 = 164 MW; h = 0,95.
Hth = H / h =225/0,95 = 236,8 m.
Q0 = P0 / (µ0 g Hth) =164 106 / (1000*9,81*236,8)=70,6 m3 s-1.
|
Examinons
le fonctionnement interne de la pompe centrifuge. L'eau est considérée
comme un fluide parfait incompressible. L'axe de la pompe est vertical,
de sorte que le fluide pompé s'écoule pratiquement dans un plan
horizontal, on négligera les effets de la pesanteur sur le fluide dans
la pompe. Trois éléments essentiels de la pompe sont :
- la roue sur laquelle sont fixées des aubes qui entraînent le fluide. Elles tournent à la vitesse angulaire w autour de son axe,
- le diffuseur, partie fixe dans laquelle le fluide est ralenti et la pression augmentée,
- la volute, en forme de spirale qui assure l'arrivée du fluide dans le réservoir récepteur.
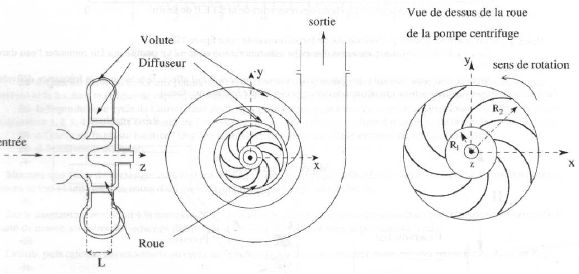
Nous n'étudierons que l'évolution du fluide dans la roue, afin
d'établir la puissance du couple qui s'exerce sur elle au cours du
pompage, en régime permanent. Il faut distinguer deux référentiels,
celui lié à la roue Rr et celui lié au corps de pompe Rp.
La roue possède N aubes; l'indice 1 est réservé aux grandeurs liées au
fluide à l'entrée de la roue, l'indice 2 aux mêmes grandeurs en sortie
de la roue. La vitesse absolue, soit la vitesse dans Rp d'une particule du fluide sera notée V, sa vitesse relative ou vitesse dans le référentiel Rr,
sera notée W. La vitesse d'entraînement d'une particule est notée U.
Les rayons intérieur et extérieur de la roues sont notés R1 et R2. La profondeur de la roue est notée L.
On adopte les coordonnées polaires pour repérer une particule le long de sa trajectoire dans le référentiel relatif.
Etude cinématique du fluide dans la roue.
Le référentiel Rp est supposé galiléen. Qu'en est-il du référentiel Rr ?
Le référentiel Rr n'est pas en mouvement retilligne uniforme par rapport à Rp : Rr n'est pas galiléen.
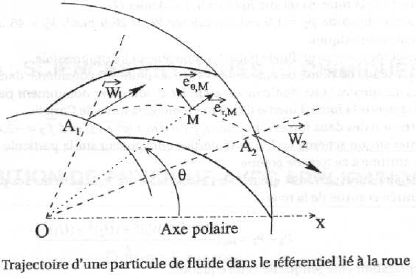
Exprimer les vitesses U1 et U2 en fonction de w, R1, R2 dans la base polaire.
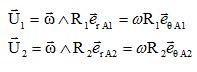
En sortie des relations similaires existent.
|
Calculer le débit volumique q1 rentrant dans la roue en empruntant le tube de courant entre deux aubes consécutives dans le référentiel Rp, en fonction de V1, R1, L, N et a1.
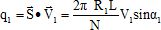
Le débit total à l'entrée vaut : Q1 = Nq1 = 2 p R1L V1 sin a1.
De même, à la sortie : Q2 = 2 p R2L V2 sin a2.
Soient les débits volumiques totaux Q'1 et Q'2 rentrant et sortant de la roue dans le référentiel Rr.
Montrer que Q1 = Q'1 et que Q2 = Q'2.
Il suffit de remplacer V1 sin a1 par W1 sin ß1 : Q'1 = 2 p R1L W1 sin ß1.
Or V1 sin a1 = W1 sin ß1 d'où Q1 = Q'1. De même Q2 = Q'2.
Montrer que Q1 = Q2.
Il y a conservation du débit volumique.
Désormais on notera Q0 le débit volumique.
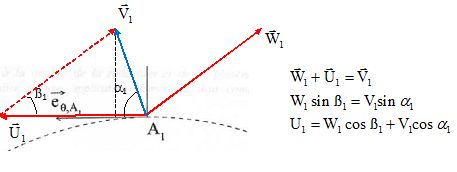
A.N : a1 = 90° ; L = 20 cm ; R1 = 1,0 m. Q0 = 71 m3 s-1. ß1 = 1,2 rad.
V1 = Q0 / ( 2 p R1L) = 71 / (6,28 *1,0*0,20) = 56,50 ~56 m/s.
W1 = V1 / sin ß1 = 56,5 / sin 1,2 =60,62 ~61 m/s.
U1 = W1cos ß1 +V1 cos 90 = W1cos ß1 = 60,62 cos 1,2 = 21,97 ~22 m/s.
w = U1/ R1 = 21,97 / 1,0 ~22 rad/s ou 22 / 6,28 =3,5 tr/s ou 2,1 102 tr/min.
Le dimensionnement de la roue est tel que R1/R2 = 0,4. Calculer U2.
U2 = w R2 = 21,97 / 0,4 =54,92 ~55 m/s.
Pour ß2 = 1,0 rad, on calcule W2 = 26,9 m/s, V2 = 46,3 m/s et a2 = 0,51 rad.
Vérifier la cohérence de ces valeurs.
V2 sin a2 = Q0/( 2 p R2L) = 71 / (6,28/0,4 *0,2)=22,61 m/s ; W2 =V2 sin a2 / sin ß2 =22,61 / sin 1,0 =26,87 ~26,9 m/s.
V2 cos a2 =U2 -W2 cos ß2 =54,92-26,87 cos 1,0 = 40,4 m/s ;
V2 sin a2 / (V2 cos a2) = tan a2 = 22,61 / 40,4 = 0,5596 ; a2 = 0,51 rad.
V2 = 22,61 / sin a2 =22,61 / sin 0,51 = 46,3 m/s.
|
Soit une particule de fluide de masse dm située au point M, considérée dans le référentiel de la roue Rr.
Faire l'inventaire des forces auquelles cette particule est soumise. Représenter ces forces sur un schéma et justifier le nom de pompe " centrifuge".
La particule est soumise à son poids, à la force d'inertie d'entraînement et à la force d'inertie de Coriolis.
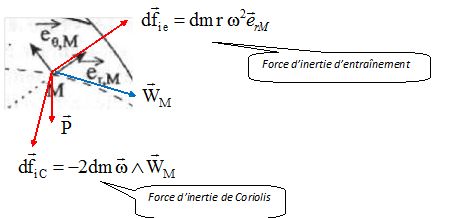
La puissance de la force de Coriolis est nulle ( la force
de Coriolis est perpendiculaire au vecteur vitesse).
Par contre la force d'inertie d'entraînement à tendance à éloigner la
particule de l'axe de rotation, d'où le qualificatif " centrifuge".
On admet la relation suivante, qui relie les pressions P1 et P2 au niveau des points A1 et A2 respectivement, aux vitesses définies en entrée et sortie de la roue.
P2-P1 = ½µ0(W12-W22 +U22 - U12).
Donner une interprétation énergétique de cette équation.
La relation de Bernoulli traduit la conservation de l'énergie le long d'une ligne de
courant.
½µ0(W12-W22 +U22 - U12) : énergie cinétique par unité de volume ou
densité d'énergie cinétique
r g (z2-z1) =0, le fluide pompé s'écoule dans un plan horizontal : densité d'énergie potentielle de
gravitation
P2-P1 : densité d'énergie élastique.
A.N : P2-P1 = 500 ( 60,622 -26,92 +54,922-21,972 ) =2,74 106 Pa.
La surface de sortie étant plus grande que la surface d'entrée, en sortie la vitesse diminue et la pression augmente.
L'étude plus avancée du fluide dans la roue permet d'établir
l'expression de la puissance du couple exercé par la roue sur le fluide
qu'elle entraîne :
Pm =Q0µ0(U2V2 cos a2 -U1V1 cos a1). Relation d'Euler des turbo-machines.
Calculer la puissance du couple.
Pm =71 *1000 (54,92 *46,3 cos 0,51 -21,97 *56,5 cos (½p) =1,58 108 W = 158 MW.
|
|