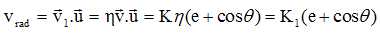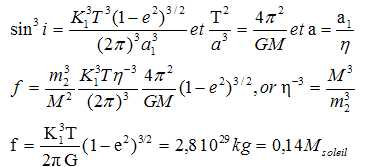.
|
Les lois de Kepler.
Enoncer les 3 lois de Kepler dans le cadre du système solaire.
1ère loi : les planètes décrivent des trajectoires elliptiques autour du soleil ; ce dernier est l'un des foyers des ellipses.
2ème loi : pendant des temps égaux le rayon vecteur balaye des aires égales.
3ème loi : le cube du demi grand axe de l'ellipse est proportionnel au carré de la période ( temps mis pour effectué une révolution ).
Décrire brièvement la démarche de keler pour aboutir à ces lois.
Kepler reprend la théorie héliocentrique de Copernic.
Kepler exploite les données de Tycho Brahe de manière empirique. Newton, 50 ans plus tard demontrera ces lois.
Montrer
que le mouvement de la particule fictive est coplanaire.
La
particule fictive P est isolée ; son moment cinétique est constant : le
rayon vecteur r est à chaque instant perpendiculaire à la direction du
moment cinétique.
Le mouvement s'effectue dans un plan perpendiculaire au moment cinétique.
Par la suite on travaillera dans ce plan et on choisira le repère polaire ( r, q) centré en G.
Démontrer la deuxième loi de Kepler, loi des aires.
On note dA l'aire balayée par le rayon vecteur durant le temps dt.
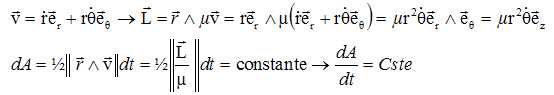
On pose C = L/µ avec L le module du moment cinétique.
Montrer que dans le cas d'une trajectoire élliptique, on a la relation : C = 2pab/T.
a
et b sont respectivement le demi-grand axe et le demi-petit axe de
l'ellipse de la particule fictive et T la période de révolution du
système binaire.
Aire de l'éllipse pab ; vitesse aréolaire dA/dt =pab/T =½C ; C = 2pab/T.
Troisième loi de Kepler : on considère le mouvement circulaire d'une masse m autour d'une masse M >> m.
Etablir que le rayon de l'orbite R et la période de révolution T sont reliés par : R3/T2 = Cste.
L'accélération est centripète dans le cas d'un mouvement circulaire.
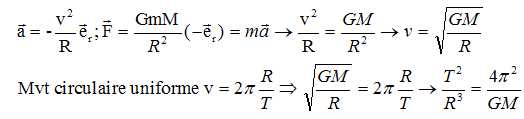
On
admettra que cette relation est valable dans le cas d'un système
binaire quelconque de trajectoire elliptique à condition de remplacer R
par le demi-grand axe a de l'ellipse et M par la masse totale du
système binaire.
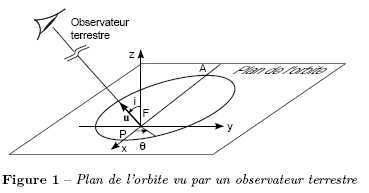
Etablir que :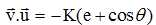
où K = C sin i / p et e est l'exentricité de l'orbite.
Dans le repère (Fxyz) :
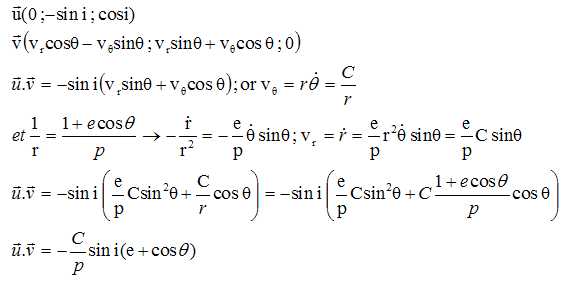
Montrer que K = 2pa sin i / (T(1-e2)½) où T est la période orbitale du pulsar.
p = C2/(GM) ; la 3è loi de Kepler donne : GM = 4 p2 a3/T2.
Or C = 2pab/T avec b = a(1-e2)½ ; par suite : C = 2pa2(1-e2)½/T.
K =C sin i / p = GM sin i / C = 2pasin i / ((1-e2)½/T).
On note v1 la vitesse du pulsar et sa vitesse radiale 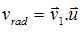 . Montrer que : . Montrer que :
vrad = -K1(e + cos q) avec K1 =2pa1sin i / ((1-e2)½/T) où a1 est le demi-grand axe de l'orbite du pulsar.
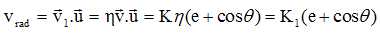
L'orbite de la particule (1) se déduit de celle de la particule fictive par une homothétie de centre G et de rapport h : a1 = ha.
|
Analyse du graphe donné par Hulse et Taylor.
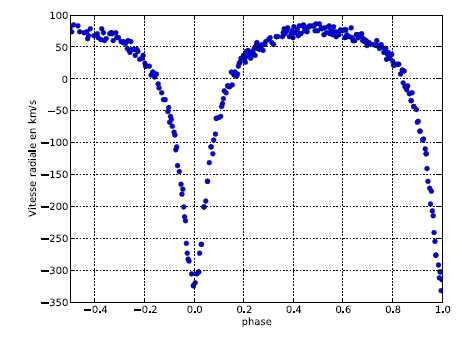
Discuter de la forme de la courbe.
D'après
la seconde loi de kepler, on remarque que la vitesse est d'autant plus
grande que la durée de passage dans une région est plus courte ( au
périastre ).
L'orbite étant une ellipse, la figure est asymétrique.
Déterminer K1 et e.
Graphiquement Vmin = -330 km/s ; Vmax =80 km/s.
Vmin = -K1(1+e) et Vmax = K1(1-e). Par suite K1 = ½(Vmax-Vmin) ~200 km/s et e = (Vmax+Vmin) / (Vmin-Vmax) ~0,61.
La période de révolution T vaut 7 h 45 min. Calculer a1 sin i.
L'expression de K1 donne : a1 sin i = K1 T(1-e2)½/ (2p) =2,0 105 *2,79 104(1-0,612)½/6,28 = 7,2 108 m.
Un paramètre important des systèmes binaires est la fonction de masse f = (m2 sin i)3/M2.
Montrer que f = TK13(1-e2)3/2 / (2pG).
A partir de l'expression de K1 et de la troisième loi de Kepler :
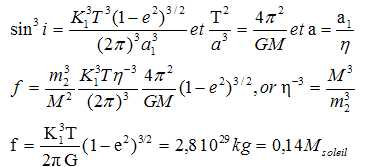
On a pu mesurer que i = 46°. Faire l'hypothèse que m1 = m2 et en déduire la masse du pulsar.
m1 = m2 = m = 4 f / sin3i = 1,5 Msoleil.
|
|
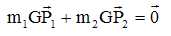
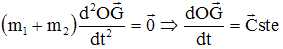
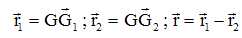
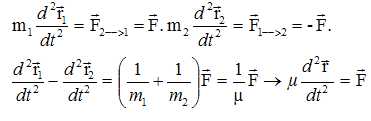
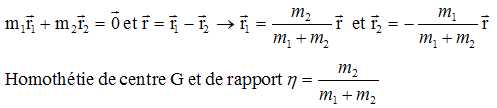
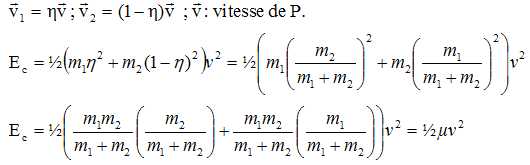
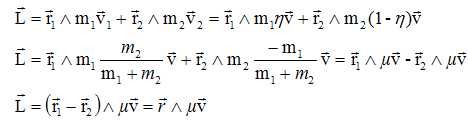
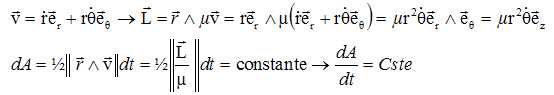
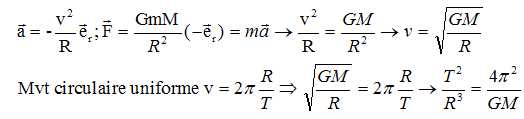

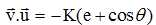
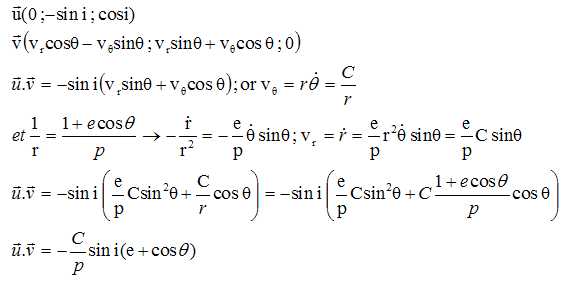
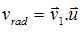 .
.