|
|
Dans le cas d'un accident nucléaire, de nombreux radionucléides
volatils, produits de fission, peuvent être relâchés. L'un d'eux est
liode 131 qui a la particularité d'être fortement assimilé par la
thyroïde, pouvant mener à des cancers de la thyroïde. En saturant
celle-ci, avant exposition, avec un autre isotope de l'iode non
radioactif, l'iode 127, par ingestion de comprimé d'iodure de potassium
KI, on observe une diminution de l'absorption d'iode radioactif d'un
facteur supérieur ou égal à 90. En pratique, les comprimés d'iodure de
potassium sont préparés par la pharmacie centrale des armées sous la
forme de plaquettes de 10 comprimés sécables dont la durée de
conservation est de 5 ans. Chaque comprimé contient 130 mg d'iodure de
potassium.
On se propose de doser, par précipitation, les ions iodures contenus
dans un comprimé de façon à vérifier la validité des comprimés, la
solution titrante étant une solution étalonnée de nitrate d'argent.
L'iodure d'argentAgI(s) est un solide ionique jaune peu soluble dans
l'eau dont le pKs vaut 16,2 à 25°C.
Ecrire l'équation de dosage et justifier qu'elle est quantitative.
Ag+aq + I-aq ---> AgI(s). K = 1 / ([Ag+aq][I-aq]) = 1/Ks = 1016,2.
K est très grand, la réaction est donc quantitative.
Par dissolution d'un comprimé d'iodure de potassium dans V0 = 100 mL d'eau, on obtient une solution S.
Dosage par conductimétrie.
On dose les ions iodures contenus dans le volume V0 de solution S à l'aide d'une solution de nitrate d'argent de concentration CAg+
= 0,130 mol/L placée dans une semi-microburette.On effectue un suivi
conductimétrique du milieu et on obtient la courbe suivante.
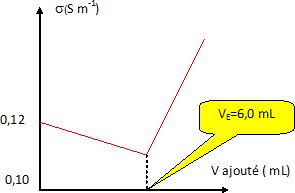
Justifier qualitativement l'allure de la courbe.
Ion
|
Ag+aq
|
NO3-aq
|
I-aq
|
K+aq
|
l( mS m2 mol-1)
|
6,19
|
7,14
|
7,68
|
7,35
|
Le volume de la solution varie peu et sera considéré comme constant.
Avant l'équivalence : l'ion argent est en défaut.
Les ions iodures disparaissent et des ions nitrates sont ajoutés. Du
point de vue de la conductivité, on remplace des ions iodure par des
ion nitrate de conductivité ionique molaire moindre. La conductivité de
la solution diminue lentement.
Après l'équivalence : l'ion argent est en excès.
On ajoute des ions argent et des ion nitrate. La conductivité de la solution croît rapidement.
|
| .
. |
.
|
Définir l'équivalence et en déduire la relation existant entre la quantité n0 d'ion iodure contenus dans un comprimé, VE et CAg+.
A l'équivalence les quantités de matière des réactifs sont en
proportions stoechiométriques. Avant l'équivalence, l'un des réactifs
est en excès, après l'équivalence, l'autre réactif est en excès. n0 = VE CAg+.
En déduire la masse m d'iodure de potassium contenu dans le comprimé. Le comprimé est-il conforme à l'inscription de la boîte ? M(KI) = 166 g/mol.
n0 = VE CAg+= 6,0 *0,130 = 0,78 mmol = 7,8 10-4 mol.
m = n0 M(KI) =7,8 10-4 *166 =0,1295 ~0,13 g ~130 mg.
Cette valeur confirme l'indication de l'étiquette.
Calculer la concentration en ion iodure de la solution S.
[I-aq] = n0 / V0 = 7,8 10-4 / 0,100 = 7,8 10-3 mol/L.
Une goutte a un volume de 0,05 mL.
Montrer qu'il y a précipitation de AgI(s) dès la première goutte versée.
Il y a précipitation dès que le produit de solubilité est atteint, c'est à dire dès que :
[Ag+aq] = Ks / [I-aq] = 10-16,2 / ( 7,8 10-3 )=8,1 10-15 mol/L.
Quantité de matière d'ion argent apportée par une goutte de solution titrante : 5 10-5 *0,130 = 6,5 10-6 mol dans V0 = 0,100 L.
[Ag+aq] = 6,5 10-5 mol, valeur bien supérieure à 8,1 10-15 mol/L.
|
Dosage par potentiométrie.
Il est aussi possible de faire le dosage des ions iodures contenus dans le volume V0
de la solution S à l'aide de la même solution de nitrate d'argent par
potentiométrie. On mesure la différence de potentiel DE entre une
électrode d'argent et une électrode de référence en fonction du volume
de nitrate d'argenr versé. On obtient la courbe suivante.
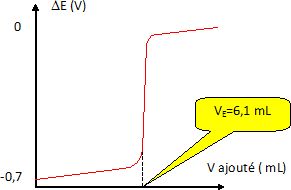
Les deux dosages donnent-ils des résultats concordants ?
n0 = VE CAg+= 6,1 *0,130 = 0,793 mmol = 7,93 10-4 mol.
m = n0 M(KI) =7,93 10-4 *166 =0,1316 ~0,13 g ~130 mg.
Les deux dosages donnent des résultats concordants. |
|

