|
|
Document 1 : présentation de l'ascenseur spatial.
Il a été envisagé dans les années 1970 comme alternative aux lanceurs
classiques de satellites que sont les fusées et navettes spatiales.
Dans certains ouvrages, l'ascenseur culminerait à l'altitude de 36000
km au-dessus du sol. Cette hauteur n'est pas due au hasard. En effet un
satellite en orbite équatoriale à cette altitude apparaît immobile au
dessus d'un point de l'équateur : c'est un satellite géostationnaire.
La particularité de l'orbite géostationnaire suggère une façon de
relier le sol et l'espace : il suffit de laisser pendre un câble d'un
satellite géostationnaire. Ce dernier restera toujours à l'aplomb du
même point de la surface terrestre d'où l'on pourra construire une base
de départ de cabines qui escaladeront le câble, transportant des
satellites directement jusqu'à l'orbite géostationnaire en quelques
jours, environ cinq selon certaines hypothèses retenues.
Et inversement les satellites en fin de vie pourraient être redescendus
par l'ascenseur et récupérés sur terre. Comment déployer le câble
depuis l'espace ? La réponse semble simple : il suffit de dérouler une
bobine de câbles préalablement mise en orbite géostationnaire.
Mais il y a un problème. Sur la partie basse du câble l'attraction
terrestre dépasse la force centrifuge due à son mouvement de rotation
autour de la terre. Conséquence : le câble est irrémédiablement tiré
vers la terre et ne peut maintenir sa position initiale. Pour pallier
ce problème, il suffit de déployer le câble simultanément dans deux
directions opposées, c'est à dire vers la terre et vers l'espace. Dans
ce cas, l'astuce consiste à ce que la partie supérieure du câble
"retienne" la partie inférieure.
L'ascenseur spatial permettrait aussi d'utiliser l'énergie de rotation
de la terre pour lancer des sondes depuis l'orbite géostationnaire vers
des orbites plus hautes. La vitesse orbitale tout en haut de
l'ascenseur serait si grande qu'un satellite qui y serait largué
n'aurait pas besoin de moteur pour échapper à l'attraction terrestre.
Vénus, Mars, Jupiter et même la sortie du système solaire seraient
accessibles sans énergie supplémentaire que celle requise pour
atteindre l'orbite géostationnaire. D'après http :
//blog.belial.fr/post/2010/04/18/Ascenseur-vers-l'espace, article de
R.Lehoucq.
Document 2 : vitesse de libération et vitesse orbitale.
La vitesse de libération VL est la vitesse minimale à
communiquer à un projectile non motorisée dans le référentiel
géocentrique ( référentiel lié au solide imaginaire contenant le centre
de la terre et trois étoiles séloignées ) pour qu'il puisse
échapper à l'attraction terrestre. Elle dépend de son altitude initiale
z.
La vitesse orbitalaire Vo d'un point due l'ascenseur
spatial, vitesse par rapport au référentiel géocentrique, qu'il possède
sur son orbite dans une direction perpendiculaire au fil de l'ascenseur.
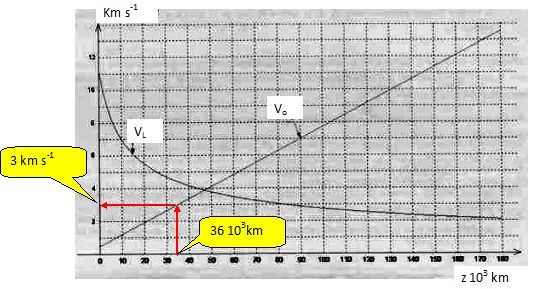
Graphe représentant la vitesse de libération et la vitesse orbitale
d'un point de l'ascenseur spatial en fonction de l'altitude z.
|
| .
. |
.
|
Pourquoi utiliser un satellite géostationnaire pour ce projet ?
D'après
les documents, définir un satellite géostationnaire puis donner les
valeurs de sa vitesse et de sa période dans le référentiel terrestre et
dans le référentiel géocentrique ?
Un
satellite géostationnaire se trouve en orbite circulaire dans le plan
équatorial de la terre à l'altitude de 36 000 km. Ce satellite tourne
dans le même sens que la terre et possède la même vitesse angulaire que
la terre. En conséquence il paraît fixe pour un observateur terrestre.
Dans le référentiel géocentrique : Vo ~3 km s-1 ; période T= 23 h 56 min.
Dans le référentiel terrestre il est immobile. V=0 ; T = 0.
Dans le référentile géocentrique, suppoosé galiléen, le satellite géostationnaire a une trajectoire circulaire.
A partir de la seconde loi de Kepler ( loi des aires), montrer que le mouvement de ce satellite est uniforme.
Le mouvement du satellite est tel que le segment de droite reliant le centre de la terre et le satellite balaie des aires égales
pendant des durées égales.
Pendant la durée dt, le segment OA balaie d'aire dA. L'angle dq étant petit, on peut assimiler le sinus à l'angle exprimé en radian.
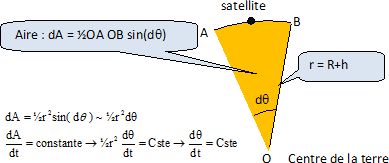
dq/dt étant constant, le mouvement est uniforme.
Donner
la direction et le sens du vecteur accélération du satellite
géostationnaire dans le référentiel géocentrique. Montrer que ces
résultats sont en conformité avec la seconde loi de Newton.
Le mouvement étant circulaire uniforme, l'accélération est centripère, dirigée vers le centre de la terre.
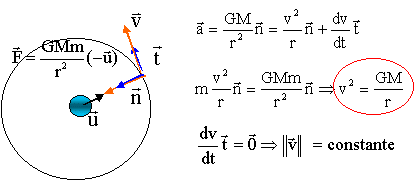
Etablir
l'expression de la vitesse v du satellite dans le référentiel
géocentrique en fonction de sa période T, du rayon R de la terre et de
son altitude h, puis calculer sa valeur. R = 6,4 103 km. T ~ 24 h ou 86400 s.
Le satellite décrit la circonférence 2p(R+h) à la vitesse v en T seconde.
v = 2p(R+h) / T = 6,28(6,4 106 + 3,6 107) / 86400 ~3,1 103 m /s.
D'après
le texte, que faut-il rajouter à un satellite géostationnaire pour
réaliser un ascenseur spatial ? Pour quelle raison est-il essentiel de
placer un satellite à 36000 km ?
Il suffit de laisser pendre un câble d'un satellite géostationnaire. Ce dernier restera toujours à l'aplomb du même point de la surface terrestre.
Un satellite en orbite équatoriale à cette altitude apparaît immobile au dessus d'un point de l'équateur.
|
L'ascenseur spatial.
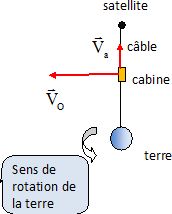
Sans souci d'échelle, représenter sur un schéma :
La terre de rayon équatorial R = 6,4 103 km ;
le satellite géostationnaire en orbite à l'altitude h = 36000 km ; le câble reliant le satellite à la terre ;
la cabine de l'ascenseur à l'altitude h' = 20 000 km ;
le vecteur vitesse ascensionnelle VA de la cabine le long du fil ainsi que son vecteur vitesse orbital VO.
Un point de l'ascenseur spatial situé à l'altitude z possède dans le référentiel géocentrique la vitesse orbitale VO(z) = 2p(R+z) / T.
Montrer
que cette expression est cohérente avec l'allure de la courbe de la
vitesse orbitale présentée dans le document ci-dessus.
VO(z) = 2pR / T + 2pz / T = A + Bz avec A = 2pR / T = constante et B = 2p / T = constante.
Il s'agit d'une fonction affine. La courbe la représentant est une
droite ne passant pas par l'origine, en accord avec le document 2.
En faisant référence au document 1, calculer la valeur de la vitesse moyenne ascensionnelle.
Distance à parcourir : 36000 km = 3,6 107 m ; durée du parcours, environ 5 jours ou 5*24*3600 =4,32 105 s.
3,6 107 /(4,32 105 ) ~83 m /s.
Comparer la vitesse ascensionnelle à la vitesse orbitale à l'altitude h'.
La vitesse orbitale à 20 km d'altitude est voisine de 2 km /s
soit environ 2/0,083 ~25 fois plus grande que la vitesse ascensionnelle.
"La vitesse tout en haut de l'ascenseur serait si grande qu'un
satellite qui y serait largué n'aurait pas besoin de moteur pour
échapper à l'attraction terrestre".
Estimer l'altitude minimale de l'ascenseur spatial pour que le satellite s'échappe de l'attraction terrestre.
Le graphe du document 1 indique que la vitesse orbitalaire devient
supérieure à la vitesse de libération à partir d'une altitude proche de
48 000 km.
Estimer l'énergie cinétique à communiquer à un satellite de masse m = 1,5 103
kg en orbite géostationnaire, pour qu'il s'échappe de l'attraction
terrestre. Comment cette énergie peut-elle lui être communiquée ?
D'après le graphe du document 1, la vitesse orbitalaire du satellite
est 3 km/s et la vitesse de libération à cette altitude est voisine de
4,5 km/s. Un moteur doit donc fournir l'énergie cinétique :
½mV2L-½mV2O = 0,5 *1,5 103 ( (4,5 103)2-(3 103)2) ~8 109 J.
|
|