|
|
Exercice 1.
On
considère une source sonore S qui se déplace rectilignement à la
vitesse v, en direction d'un récepteur immobile au point O. S émet des
bips sonores qui se succèdent périodiquement : soit f la fréquence
d'émission et T la période correspondante. On note d la distance qui
sépare S de O, à la date t1 d'émission du premier bip
sonore. Le son se propage à la célérité c.
Donner
la relation entre T et f.
La période T ( s) est égale à l'inverse de la fréquence f (Hz) : T =
1/f.
Ecrire t' la date de
réception du premier bip en O.
Le son parcourt la distance d à la célérité c : t' = d /c + t1.
Ecrire t" la date de
réception du premier bip en O.
La source parcourt la distance vT en T seconde.
Distance entre la source S et O lors de l'émission du second bip : d2
=d-vT
Le son parcourt la distance d2
à la célérité c : t" = d2 /c + t1+ T = (d-vT) / c+
t1+ T
Ecrire T ' la
période du son reçu en O.
T ' = t"-t' =(d-vT) / c+
t1+ T-(
d /c + t1)
T ' =T -vT / c = T
( 1-v/c).
En
déduire la fréquence f' de la succession des bips sonores reçus en O en
fonction nottament de f.
f ' = 1/T '
= f c / (c-v)).
Sans justifier,
donner l'expression de la fréquence f' pour une source qui
s'éloignerait du récepteur.
Le sens positif des vitesses est celui de la propagation du son.
Changer le signe de v, si la source s'éloigne de O : f ' =
f c / (c+v)).
|
.
analyse de l'effet Doppler.
Une source S, qui émet des " bips " à la période T se d�éplace
à vitesse constante vs vers un observateur fixe situé en O.
Le bip se propage à la célérité c dans l'air. A l'instant initial (t =
0), la source (distante de d1 du point O) émet son premier
bip.
A quel instant t1
l'observateur reçoit-il le premier bip ?
t1 = d1/c.
La source émet, tout en se déplaçant, des bips
régulièrement avec une période T.
A quelle distance d2 de
l'observateur se trouve la source lorsqu'elle émet son deuxième bip
?
d2 = vsT.
A quel instant t2 (compté
depuis l'émission de premier bip) l'observateur reçoit-il son deuxième
bip ?
t2 =T+ d2/c = T
+vs/cT.
Trouver une relation entre la période T'
des bips reçus par l'observateur et la période T des bips émis pas la
source.
T' = t2-t1 = T (1-vs/c).
Déterminer ensuite la relation entre la
fréquence ƒ' et la fréquence ƒ émise ?
La fréquence est l'inverse de la période : f'
= (c-vs ) / c f.
Le spectre de la lumière des galaxies lointaines est décalé vers le
rouge et ce décalage augmente avec la distance des galaxies au système
solaire.
Peut-on appliquer à la lumière l'étude
précédente ? Si oui, donner une explication à ce phénomène.
L'effet Dopler s'applique à la lumière.
Les fréquences des radiations rouges sont plus petites que celles de la
lumière visible.
Or f' = (1-vs/c) f conduit à f ' < f , décalage vers des
fréquences plus faibles.
Mesure du débit sanguin.
On
souhaite mesurer le débit sanguin dans une veine en mettant à profit
l'effet Doppler. La sonde fonctionne en mode pulsé à la fréquence f =
4,3 MHz. On se place dans le cas où l'épaisseur du milieu ( peau
graisse ) est négligeable devant celle de la veine. La célérité des
ultrasons dans le sang est c = 1,5 103 m/s.
Définir succinctement l'effet Doppler.
La fréquence reçue par un récepteur est différente de la fréquence émise par un
émetteur quand émetteur et récepteur sont en mouvement relatif.
L'effet Doppler est le décalage de fréquence entre la mesure à
l'émission et la mesure à la réception lorsque l'émetteur et le
récepteur sont en mouvement relatif.
L'écart en fréquence est donné par la relation : fr-f0 = 2 v cos q / c f0.
Définir tous les termes de cette relation.
fr : fréquence ( Hz) de l'onde réfléchie ; f0 : fréquence (Hz) de l'onde incidente ;
v : vitesse (m/s) du sang ; c : célerité ( m/s) des ultrasons ; q : angle formé entre les directions de la veine et le faisceau d'ultrasons
Calculer la vitesse du sang pour fr-f0 =0,50 kHz et q = 60°.
v =c(fr-f0 ) / (2f0 cos q ) = 1500*500 / (2*4,3 106 *cos60)=0,1744 ~0,17 m/s.
Pour quelle valeur de q, cet écart serait théoriquement maximum ? Cette valeur est-elle réaliste en pratique ?
Si q=0, cos q= 1 : en pratique il est impossible que le faisceau d'ultrasons ait la même direction que la veine.
Les ondes ultrasonores sont déviées à l'interface de deux milieux : sin i1 / c1 = sin i2 / c2.
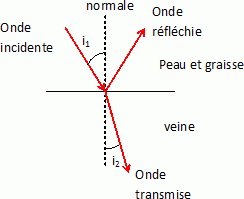
Si i1 = 30 °, calculer i2.
sin i2 = c2 sin i1 / c1 =1,5 103 *sin 30 / 1,4 103=0,536 ; i2 =32,3 ~32°.
Comparer les valeurs de i1 et i2. En déduire si le phénomène de réfraction est préjudiciable pour déterminer la vitesse du sang dans la veine.
Les angles i1 et i2 sont à peu près identique ( à 6 % près ). La réfraction n'est donc pas préjudiciable pour déterminer la vitesse du sang.
|
|
