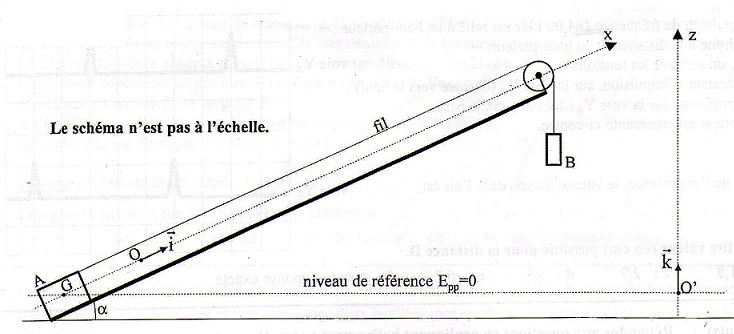
Solide sur un plan incliné : concours kiné Berck 2012.

. .

Répondre aux questions en expliquant brièvement votre démarche. Un solide A de masse M peut glisser suivant la ligne de plus grande pente d'un plan incliné d'un angle a par rapport à l'horizontale. Il est relié par un fil inextensible et de masse négligeable à un solide d'entraînement B de masse m. Le fil passe sur une  poulie sans frottement et de masse négligeable. On admmettra que la valeur de la tension du fil est la même de part et d'autre de la poulie. On négligera l'action de l'air sur les solides A et B. Le solide A est soumis sur le plan incliné à une force de frottement s'opposant au mouvement et de valeur constante f inconnue. L'abscisse x du centre d'inertie G du solide A est repéré sur un axe ascendant dont la direction est parallèle au plan. L'origine des dates est choisie à l'instant ou G passe en O. Un dispositif informatisé a permis pour deux positions différentes de mesurer plusieurs grandeurs relatives au solide A. Grandeur Position 1 Position 2 date t ms) 400 800 abscisse x (cm) 33,9 76,4 énergie cinétique (mJ) 343 517 énergie potentielle ( J) 1,83 2,76 M =752 g ; m = 325 g. . . . Déterminer la valeur de l'angle a. Altitude h1 de G à la position 1 : Epp1 / Mg =1,83 / (0,752*9,81)=0,248 m. Altitude h2 de G à la position 2 : Epp2 / Mg =2,76 / (0,752*9,81)=0,374 m. sin a = (h2-h1) / (x2-x1) =(0,374-0,248) /(0,764-0339) =0,126 / 0,425 =0,2964 ; a =17,25 ~17,2°. Calculer la valeur de l'accélération a du solide. Vitesse v1 de G à la position 1 :( 2Ec1 / M )½=(2*0,343 /0,752)½=0,95511 m/s. Vitesse v2 de G à la position 2 :( 2Ec2 / M )½=(2*0,517 /0,752)½=1,1726 m/s. a =(v2-v1) /(t2-t1)= (1,1726-0,95511) / 0,400=0,5437  0,544 m s-2. En déduire la valeur de la force de frottement f ( en mN). 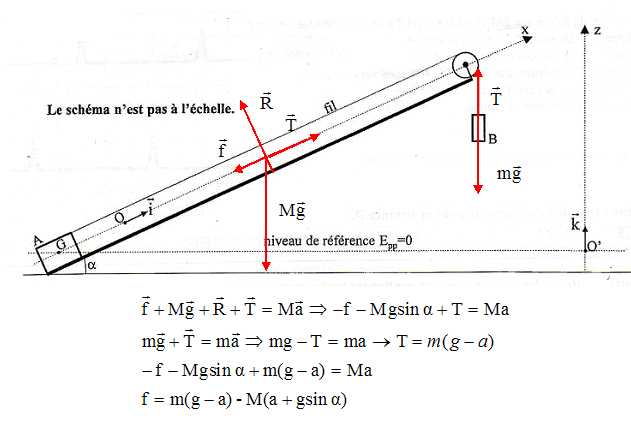f= 0,325(9,81-0,544)+0,752(0,544+9,81 sin17,2)= 0,421 N = 421 mN. Déterminer la valeur de la vitesse v0 à la date t=0. x(t) = ½at2 +v0t ; v0 = x(t) / t -½at = 0,339 / 0,400 -0,5*0,544*0,400 =0,739 m/s. ou bien : v0 = x(t) / t -½at = 0,764 / 0,800 -0,5*0,544*0,800 =0,738 m/s. Déterminer la valeur de l'énergie cinétique à la date t = 600 ms. v = at + v0 =0,5436 *0,600 +0,739 =1,0652 m/s. ½Mv2 =0,5*0,752*1,06522 =0,427 J.

menu