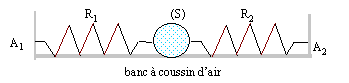
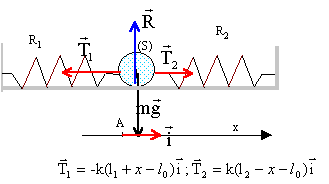
Solide maintenu par deux ressorts identiques : concours Audioprothésiste Nancy 2004.

. .

. Un solide S de masse m reposant sur un banc à coussin d'air est maintenu par deux ressorts identiques de raideur k. La position du centre d'inertie G de S est repérée au cours du temps par son abscisse x(t) sur un axe Ox horizontal. Les deux ressorts restent étirés au cours du mouvement. L'origine O de l'axe correspond à l'abscisse de G à la position d'équilibre. Les deux ressorts étant identiques : l1=l2. l1+l2+ 2R= L ; A1A = A2A = l1+ R = ½L = 37,5 cm. longueur de R1 : l1+x = ½L-R+x longueur de R2 : l2-x = ½L-R-x la seconde loi de Newton s'écrit en projection sur l'axe Ax : -T1 + T2 = mx" -k(½L-R+x-l0) + k(½L-R-x-l0)=mx" 2kx=mx" soit x" + 2k/m x=0 on pose w²= 2k/m ; w = 2pf soit f = 1/(2p)[2k/m]½ ; T= 1/f = 2p[2k/m]-½ . . Montrer que la fonction x(t) = A cos ( 2pt / T +f) , où A et f sont des constantes, est solution de l'équation différentielle pour une expression particulière de T que l'on précisera. x'(t) = -A 2p/ T sin ( 2pt / T +f) ; x"(t) = -A (2p/ T)2 cos ( 2pt / T +f) = -(2p/ T)2 x(t). Repport dans l'équation différentielle : -(2p/ T)2 x(t) + k/m x(t) = 0, égalité vérifiée quel que soit le temps si : (2p/ T)2 = k/m ; T = 2 p (m / k)½. Calculer T. On donne m = 900 kg ; k = 2,25 104 N m-1. T = 2*3,14 ( 900 /(2,25 104) )½ =1,256 ~1,26 s. On appelle vx(t) la coordonnée du vecteur vitesse du mouvement du solide S sur l'axe Ox. A l'instant t=0, un choc est donné au solide S. Il possède alors une vitesse vx(0) = 1,5 m/s. On supposera qu'à cet instant t=0, x(0) = 0. Etablir les valeurs des constantes A et f ainsi que l'expression numérique de x(t). Que représente la constante A ? x(0) = A cos ( f) = 0 soit, A: amplitude non nulle, f = +½p ou -½p. x'(0) = -A 2p/ T sin ( f) = vx(0) = 1,5 m/s. A 2p/ T étant positif, alors f = -½p. A 2p/ T = vx(0)  ; A = vx(0) T / (2p) =1,5 * 1,256 / 6,28 ~0,30 m. x(t) = 0,30 cos (5 t -½p) =0,30 sin (5 t ). Tracer l'allure de la courbe x(t).( sans graduer les axes ). .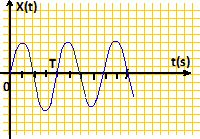

menu