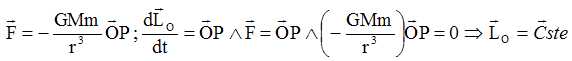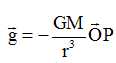Vaisseau spatial dans un champ newtonien : concours ITPE 2012

Aurélie 02/10/12

Vaisseau spatial dans un champ newtonien : concours ITPE 2012.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

.

On considère un vaisseau assimilé à un point matériel noté P, de masse m, mobile par rapport à un astre de masse M, de centre O et de rayon R. Le champ de gravitation de cet astre est à symétrie sphérique. La constante de gravitation est notée G. La distance entre le vaisseau et le centre de l'astre est notée r > R. On se placera dans le référentiel ( supposé galiléen ) lié à l'astre. Sauf mention contraire, le meteur de la fusée est éteint, c'est à dire que le vaisseau est en vol balistique.
Montrer que le moment cinétique ( calculé en O) du vaisseau est une constante du mouvement.
L'interaction de type newtonienne s'exprime sous la forme k/r². ( k est une constante). Les forces newtoniennes sont des forces centrales. Ecrire le théorème du moment cinétique en O :

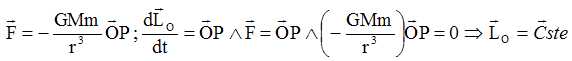
Cette constance de L₀ a deux conséquences sur la trajectoire du vaisseau. Lesquelles ?
Le moment cinétique étant un vecteur constant, la trajectoire est plane, contenue dans un plan perpendiculaire au vecteur moment cinétique.
La trajectoire est parcourue suivant la loi des aires. Dans un mouvement à force centrale, le rayon vecteur balaie des aires égales pendant des durées égales.
Donner l'expression du champ gravitationnel crée par un astre en un point P extérieur à l'astre à la distance R de O.

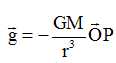
Quelle est l'expression de l'énergie potentielle E_p du vaisseau en la choisissant nulle à l'infini ? Que devient cette expression au niveau du sol ?
A la distance r de O : E_p = -GMm / r. Au niveau du sol : E_{p sol}= -GMm / R.
Or g₀ = GM/R² ; GM = g₀ R² ; E_{p sol}=- g₀ R²m / R = -g₀ R m.
Dans le cas d'une orbite circulaire de rayon r₀, exprimer l'énergie mécanique E_m du vaisseau et sa période de révolution T_rev en fonction de g₀, R, r₀ et, si nécessaire de m. Commenter le signe de E_m.
Dans le cas d'une orbite circulaire, le mouvement est uniforme, la norme de la vitesse est constante.
Energie cinétique : E_c = ½mv² avec v² = GM/r₀ ; E_c = ½mGM/r₀ ;
E_m = E_p+E_c = -GMm / r₀ + ½mGM/r₀ = -½mGM/r₀.
Le satellite décrit la circonférence 2pr₀ à la vitesse v en T_rév secondes.
2pr₀ = v T_rév =(GM/r₀)^½ T_rév; T_rév = 2p r₀^1,5/(GM)^½.
L'énergie mécanique est négative : le satellite reste lié à la terre.
Dans le cas de la terre, on considère une masse m = 1 kg, initialement au repos à la surface de la terre ( R = 6400 km), puis placée en orbite circulaire de rayon r₀ = 7000 km. En prenant g₀ = 10 m s^-2, évaluer numériquement la différence d'énergie mécanique DE_m entre ces deux états.
Au niveau du sol : E_{M sol} = -½mGM / R ; à l'altitude h = 7000 km : E_{M h} = -½mGM / r₀.
DE_m = E_{M h}- E_{M sol}= -½m GM( 1/r₀- 1/R) = ½m GM (r₀-R) / (r₀R).
Or g₀ R² = GM : DE_m =½m g₀ R(r₀-R) / r₀.
DE_m =0,5 *10*6,4 10⁶ *6,0 10⁵ / (7,0 10⁶) =2,7 10⁶ J ou 2,7 10⁶ / ( 3,6 10⁶) ~ 0,75 kWh
1 kWh électrique revient environ à 0,15 € ; en déduire numériquement le coût théorique de la satellisation d'un kg de charge utile. Le coût réel est de l'ordre de 1000 € par kg. Commenter ces valeurs.
Coût théorique ~ 0,10 €, très nférieur à 1000 €.
Dans la réalité il faut prendre en compte les frottements sur les couches d'air de l'atmosphère lors du lancement de la fusée. Il faut de plus propulser la fusée, carburant, comburant et prendre en compte le coût du matériel.

.
.

.

.

On peut montrer que la trajectoire d'un vaisseau ( moteur coupé ) dans le champ gravitationnel de l'astre est une conique, d'équation polaire 1/r = (1+e cos q) p,où e est l'exentricité de la conique et p le paramètre. On se limitera ici au cas où la trajectoire est fermée, donc elliptique.
Dessiner l'allure de la trajectoire du satellite en plaçant l'astre attracteur, l'apogée, le périgée. Exprimer le demi-grand axe "a" en fonction de e et p.

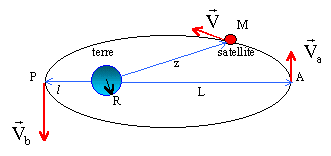
A : apogée ; P : périgée.
r_apogée = p / (1-e) et r _périgée = p / (1+e) ; a = ½(r_apogée+r _périgée) = ½p( 1/(1-e) +1/(1+e) = p/(1-e²).
Donner l'expression de la 3^ème loi de Kepler.
T²/a³ = 4p²/(GM).
Supposons qu'à une distance r₀ du centre de l'astre, la norme V de la vitesse d'un vaisseau soit le même que pour une orbite circulaire mais que l'angle a entre le support de la vitesse et la tangente au cercle de centre O et de rayon r₀ appartienne à [0 ; ½p]. Quelle est la nature de la trajectoire du vaisseau ?
La vitesse et la distance sont identiques à celle d'un mouvement circulaire : l'énergie est donc la même. La trajectoire sera elliptique de demi-grand axe a = r₀.
En utilisant la relation entre le demi-grand axe "a" de la trajectoire et l'énergie mécanique du vaisseau, déterminer l'expression de "a" en fonction de r₀ et a.
Le point de la trajectoire étant à la distance "a" du foyer de l'ellipse, il se trouve sur l'un des sommets du petit axe de l'ellipse.

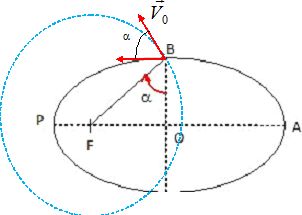
e = c / a = OF / BF = sin a ; or a = p/(1-e²) ; r_A = a+c = a(1+e) ; r_P = a-c = a(1-e) ; a = r₀.
Par suite p = r₀(1-sin²a) = r₀ cos²a ; r_A = r₀(1+sin a) ; r_P = r₀(1-sin a).
Quelle est l'expression de la constante des aires de la trajectoire, notée C, en fonction de r₀, V et a ? En utilisant l'expression du paramètre p de la conique en fonction de la constante des aires, g₀ et R, déterminer l'expression de p en fonction de r₀ et a.
En utilisant l'expression de"a" en fonction de p et de l'excentricité e de la trajectoire, déterminer l'expression de e en fonction de r₀ et a.
En utilisant les expressions des distances r_A du centre O à l'apogée et r_P du centre O au périgée, en fonction du paramètre e et du paramètre p, déterminer les expressions de r_A et r_P en fonction de r₀ et a.

Vitesse de libération.
Le vaisseau est initialement sur une orbite circulaire de rayon r₀ décrite à la vitesse V₀. On allume le moteur pendant un temps très court, de sorte que la vitesse varie mais pas la distance au centre de l'astre.
Evaluer la vitesse V₁ minimale qu'il faut communiquer au vaisseau pour qu'il échappe au champ gravitationnel de l'astre en fonction de G, M et r₀.
Si l'énergie mécanique du vaiseau devient positive, ce dernier échappe au champ gravitationnel de l'astre.
½mV₁²-GMm/r₀ >=0 ; V₁ >= (2GM / r₀)^½.
Le commandant de bord dispose d'un "budget de vitesse " DV = 4V₀ ; cela signifie que la quantité de carburant disponible lui permet de faire varier la vitesse du vaisseau, en une ou plusieurs fois, pourvu que la somme des valeurs absolues des variations de vitesse n'excèdent pas 4 V₀.
Option 1 : le commandant utilise tout son budget d'un seul coup en amenant sa vitesse initiale à 5 V₀.
Evaluer sa vitesse finale à l'infini en fonction de V₀.
Conservation de l'énergie mécanique entre l'instant de départ et l'infini : ½m(5V₀)²-GMm / r₀ = ½m V²_infini.
Or sur une orbite circulaire : mV₀²/r₀ = GMm/r₀² ou GMm / r₀ =mV₀².
Par suite : ½m(5V₀)²-mV₀² = ½m V²_infini ; 23 V₀²= V²_infini; V_infini = (23V₀)^½.
Option 2 : on utilise 1/8^è du budget pour ralentir le vaisseau de V₀ à ½V₀ en un temps très court devant la période, le vecteur vitesse gardant la même direction.
Décrire la nouvelle trajectoire : le demi-grand axe "a", les distances r_A et r_P, les normes des vitesse V_A et V_P en fonction de r₀. Quelle condition doit vérifier r_P ?
A une distance égale au grand axe, l'énergie mécanique est égale à l'énergie potentielle.
Conservation de l'énergie mécanique : ½m(0,5 V₀)²-mGM/r₀ =- mGM / (2a).
Or sur une orbite circulaire : mV₀²/r₀ = GMm/r₀² ou GMm / r₀ =mV₀².
D'où : GMm / (8r₀) -mGM/r₀ =- mGM / (2a) soit : 1/ r₀ -1/ (8r₀) = 1 / (2a) ; 7/(8r₀) = 1 / (2a) ; 7/(4r₀) = 1 / a ; a = 4r₀/7.
Au périgée et à l'apogée le rayon vecteur est perpendiculaire à la vitesse. Le point de départ de la manoeuvre est l'apogéee : r_A = r₀ ; V_A = ½V₀.
2a = r_P + r_A ; r_P = 8r₀/7-r₀ = r₀/7.
Conservation du moment cinétique entre l'apogée et le périgée : r_AV_A = r_PV_P ; V_P = r₀½V₀ / (r₀/7) = 3,5 V₀.
Il faut bien sûr que le rayon de l'astre soit inférieur à r_P pour éviter l'impact sur la planète.
On utilise ensuite le reste du budget vitesse au passage au périgée pour augmenter au maximum la vitesse du vaisseau. Justifier la nouvelle trajectoire et déterminer la vitesse finale ( à l'infini )en fonction de V₀.
Conservation de l'énergie entre le périgée et l'infini :
½m(7V₀)²-GMm / (r₀/7) = ½m V²_infini.
Or sur une orbite circulaire : mV₀²/r₀ = GMm/r₀² ou GMm / r₀ =mV₀².
Par suite : ½m(7V₀)²-7mV₀² = ½m V²_infini ; 35 V₀²= V²_infini; V_infini = (35V₀)^½.
L'énergie du vasiseau étant devenu positive, la nouvelle trajectoire est une branche d'hyperbole.
Comparer les deux options et commenter.
L'option 2 permet d'obtenir une vitesse plus importante à l'infini. Il est plus efficace de produire une variation de vitesse près d'un astre que très loin de lui.

menu