|
|
On désire étudier le comportement d'un
circuit RLC série. On dispose d'un
générateur basse tension ( GBF), d'un
oscilloscope, d'un ampèremètre (A) et d'un
voltmètre ( V). R = 500 ohms ; L = 0,300 H ; C = 20,0 nanofarad.
Le GBF délivre une tension alternative sinusoïdale u(t) = Um sin (wt).
Faire figurer les branchements de l'oscilloscope permettant d'obtenir l'oscillogramme ci-dessous.
On visualise à l'aide d'un oscilloscope la tension aux bornes du générateur sur la voie B ( 2 V / div ) ainsi que celle uR(t) aux bornes du conducteur ohmique R sur la voie A( 0,5 V/ div ).
Quelle est l'amplitude Umax de u(t) ? Quelle est la valeur maximale Imax de l'intensité du courant i(t) ?
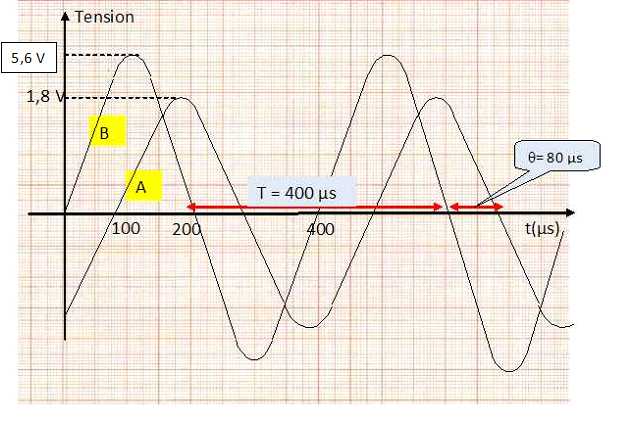
URmax = RImax = 1,8 V ; Imax = URmax / R =1,8 / 500 =3,6 10-3 A.
Calculer l'impédance Zexp du dipole à partir des valeurs expérimentales.
Zexp = Umax / Imax = 5,6 / (3,6 10-3) =1,56 103 ~ 1,6 103 ohms.
Déterminer la période T et en déduire la fréquence f des tensions.
T = 400 µs = 4,0 10-4 s ; f = 1/T = 1/(4,0 10-4) =2,5 103 Hz.
Indiquer si u(t) est en avance ou en retard de phase sur i(t).
Lorsque
les deux sinusoïdes varient dans le même sens, la première qui passe
par un maximum est en avance sur l'autre. B est en avance sur A : u(t)
est en avance sur i(t).
Montrer que le déphasage f de u(t) sur i(t) vaut 0,40 p rad.
q = 80 µs ; T = 400 µs ; q =0,2 T.
Or une période correspond à 2 p radians : f = 0,2*2p = 0,40 p rad.
|
.
.
On
maintient la valeur de la tension efficace aux bornes du générateur
constante U = 4,0 V et on effectue un balayage en fréquence : on relève
les valeurs lues sur l'ampèremètre. On obtient la courbe suivante
représentant l'évolution de l'intensité efficace I du courant en
fonction de la fréquence.
Donner les valeurs de l'intensité efficace I0 et de la fréquence f0 correspondant au sommet de la courbe.
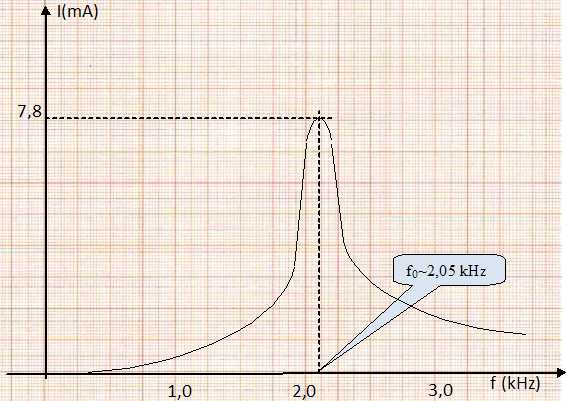
I0 = 7,8 10-3 A et f0 = 2,05 kHz.
De quel phénomène s'agit-il ? Résonance d'intensité.
Calculer la valeur de l'impédance Z0 correspondant au sommet de la courbe. Comparer cette valeur à R et proposer une explication pour interpréter la différence.
Z0 = U/I0 = 4,0 / (7,8 10-3)=5,13 103 ~5,1 103 ohms, valeur un peu supérieure à R. la résistance de la bobine n'est pas nulle mais voisine de 10 ohms.
Lorsque la courbe de réponse atteint son maximum, quel est le déphasage entre u(t) et i(t) ?
u(t) et i(t) sont en phase à la résonance d'intensité.
|
.
|