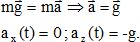Il
s'agit dans cet exercice de chercher l'ordre de grandeur des vitesses
d'éjection de blocs de matière émis lors de cette éruption volcanique
et de déterminer l'altitude maximale atteinte par un bloc dans une
situation donnée.
|
|
On
considère dans le référentiel terrestre supposé galiléen, un bloc de
matière de masse m. Ce bloc est assimilé à un point matériel. l'origine
des dates est l'instant où le bloc quitte le point O.

On néglige la poussée d'Archimède et les forces de frottement dues à l'air. On prendra g = 9,8 m s-2.
Equations horaires du mouvement.
Pourquoi peut-on dire que le bloc est en cghute libre ?
La
poussée d'Archimède et les forces de frottement dues à l'air étant
négligées, le bloc n'est soumis qu'à son poids : la chute est donc
libre.
En
appliquant la seconde loi de Newton, établir la relation entre le
vacteur accélération du centre d'inertie du bloc et le vacteur champ de
pesanteur puis donner l'expression des composantes ax(t) et az(t) dans le repère d'étude.
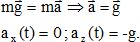
En déduire les expressions littérales vx(t) et vz(t) du vecteur vitesse du bloc.
Le vecteur vitesse est une primitive du vecteur accélération.
vx(t) = Constante ; vx(0) = v0 cos a donc vx(t) =v0 cos a.
vz(t) = -gt + constante ; vz(0) = v0 sin a donc vz(t) = -gt +v0 sin a.
Montrer que les expressions des équations horaires du mouvement x(t) et z(t) sont :
x(t) =v0 cos a t et z(t) = -½gt2 +v0 sin a t.
Le vecteur position est une primitive du vecteur vitesse et la position
initiale est confondue avec l'origine du repère. Les constantes
d'intégration sont donc nulles.
Par suite : x(t) =v0 cos a t et z(t) = -½gt2 +v0 sin a t.
Bloc éjecté du cratère avec une vitesse initiale verticale v01.
Texte 1
: les observations les plus directes concernent la hauteur h
atteinte par de gros blocs lancés verticalement lors de l'éruption. de
cette hauteur h, on tire la vitesse v = (2gh)½.
L'épouvantable éruption de la Montagne Pelé n'a réussi à lancer des
pierres de volume un peu considérable qu'à 400 m. D'après le
Journal des Observateurs ( janvier 1940).
Préciser les expressions de vx(t), vz(t), x(t) et z(t) dans la situation étudiée.
a = 90 ° ; sin 90 = 1 et cos 90 = 0, d'où :
vx(t) = 0 ; vz(t) = -gt + v01 ; x(t) = 0 ; z(t) = -½gt2 + v01t.
A partir de l'expression de vz(t), déterminer l'expression littérale de la date tS à laquelle l'altitude maximale est atteinte.
vz(tS) = 0 ; -gtS + v01 =0 ; tS = v01/ g.
En déduire que l'expression de la vitesse initiale est v01 = (2gh)½.
Repporter tS = v01/ g dans l'expression de z(t) :
z(tS) = h = -½g(v01/ g)2 + v01(v01/ g) = -½v012/g + v012/g = ½v012/g ; v012 = 2gh ; v01 = (2gh)½.
Calculer v01 si h = 400 m.
v01 = (2*9,8*400)½ = 88,54 ~89 m/s.
|
.
.
Bloc éjecté du cratère avec une vitesse initiale oblique v02.
Texte 2 :
Nous avons, pour cette éruption, un cas observé le 7 mai 1902, où la
trajectoire parabolique " d'énormes roches nettement visibles" peut,
d'après les données notées par un témoin oculaire, être grossièrement
calculée. la vitesse initiale était environ 110 m/s et elle était
inclinée sur l'horizon de 43°. D'après le Journal des Observateurs ( janvier 1940).
Le point d'impact A est situé sur le flanc du volcan 800 m plus bas que
le point O. Le bloc a parcouru horizontalement une distance environ
égale à 1,8 km.
Etablir l'expression de la trajectoire.
x(t) =v02 cos a t soit t = x / (v02 cos a) ; repport dans l'expression de z(t) :
z(t) = -½g[ x / (v02 cos a)]2 +v02 sin a x / (v02 cos a).
z(t) = -½g x2 / (v02 cos a)2 + x tan a.
En déduire l'expression littérale de v02. Calculer sa valeur et la comparer à celle indiquée dans le texte 2.
x tan a -z(t) = ½g x2 / (v02 cos a)2 ; (v02 cos a)2 =½g x2 /( x tan a -z(t)) ;
v022 = ½g x2 /[( x tan a -z(t)) cos a)2]
v02 = x / cos a [½g / ( x tan a -z(t))]½.
v02 =1,8 103 / cos 43 [0,5*9,8 / (1,8 103 tan 43 -(-800)]½ ;
v02 =2461,2 * [4,9 / 2478,5]½ = 109,4 ~1,1 102 m/s, valeur en accord avec celle indiquée.
On suppose que l'énergie mécanique du système se conserve. La masse m du bloc ejecté est égale à 500 kg.
Exprimer littéralement puis calculer les valeurs initiales des énergies cinétique, potentielle et mécanique du bloc.
On choisit une énergie potentielle nulle pour z = 0 : l'énergie potentielle initiale mgz est nulle.
Energie cinétique initiale: ½mv022 =0,5 *500 *1102 = 3,025 106 ~3,03 106 J.
L'énergie mécanique est la somme des énergies cinétique et potentielle : mgz + ½mv022 =3,03 106 J.
Déterminer
les valeurs de l'énergie cinétique et de l'énergie potentielle du bloc
au point le plus élevé de la trajectoire noté C.
En C la composante verticale de la vitesse est nulle : vC = v02 cos 43 = 110 cos 43 = 80,45 m/s.
Energie cinétique en C : ½mvC2 = 0,5*500 *80,452 = 1,618 106 ~1,62 106 J.
L'énergie mécanique se conserve ; l'énergie potentielle en C vaut : 3,025 106 - 1,618 106 = 1,407 106 J ~1,4 106 J.
En déduire l'altitude h' maximale atteinte.
1,407 106 = mg h' ; h' = 1,407 106 / (mg ) = 1,407 106 / (500*9,8 ) ~2,9 102 m.
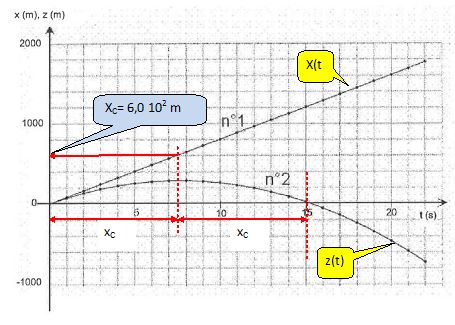
Identifier les courbes x(t) et z(t) et déterminer graphiquement la distance xC parcourue horizontalement par le bloc lorsqu'il atteint son altitude maximale.
x(t) =v02 cos a t : équation d'une droite.
z(t) = -½g x2 / (v02 cos a)2 + x tan a : équation d'une parabole.
|
|