.
|
|
Etude
du moteur asynchrone triphasé.
Le moteur qui équipe le shredder est un moteur triphasé asynchrone dont
les caractéristiques sont rassemblées ci-dessous : puissance absorbée Pa
=2,5 103 kW ; tensions d'alimentation 7500 /
13000 V ; vitesse nominale nn = 1440 tr/min ;
facteur de puissance ks = 0,80. Résistance
mesurée entre phases aux bornes du moteur : R = 1,11 ohms ; pertes
magnétiques stator : Pf =83,3kW ; pertes
mécaniques Pm =87,2 kW.
Il est alimenté par un réseau de tension triphasée 4300 V / 7500 V ; 50
Hz. L’étude se fait en fonctionnement nominal.
Couplage
:
Quel
est la nature du couplage du moteur au réseau ? Justifier la réponse.
La tension maximale
que peut supporter un enroulement correspond à la plus petite des
tensions indiquées sur la plaque signalétique; soit 7500 V.
Pour
un couplage triangle,
la tension aux bornes d'un enroulement correspond à une tension
composée.
Compléter
le schéma en représentant le couplage du moteur et sa
connexion au réseau.
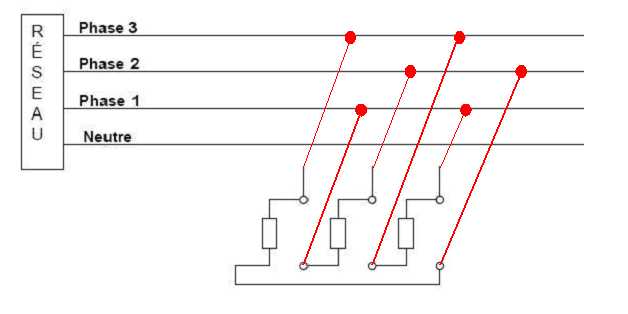
Déterminer
le nombre de pôles et la vitesse de synchronisme ns.
ns est légèrement supérieure à nn
; ns = 1500 tr/min = 1500/60 =25 tr/s ; p = f / ns
= 2 paires de pôles.
Calculer
le glissement g du moteur.
g = 1-nn / ns =
1-1440/1500 =0,040 (4,0 %)
Montrer
que l'intensité du courant qui arrive aux bornes du moteur est égale à
I = 241 A ; en déduire l'intensité J qui traverse un enroulement du
stator.
Pa = 3½U I ks
; I = Pa
/( 3½U ks ) =2,5 106
/ (1,732*7500*0,80) =241 A.
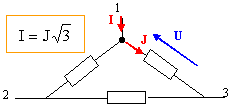
Chaque
impédance est alimentée sous une tension composée
; l'intensité du courant dans un fil de ligne I diffère de
l'intensité du courant J dans une impédance.
J
=IN /3½ =241 / 1,73
=41,97 = 139,14 ~139
A.
Calcul des pertes.
Calculer
la puissance perdue par effet Joule au stator, PJS.
PJS =
3 R J2 = 3*1,11*139,142
=64465 W ~64,5 kW.
Montrer
que la puissance transmise du stator au rotor, Ptr, prend la
valeur de 2,32 x 103 kW.
Ptr = Pa -PJS
-Pf= 2,5 103-64,5
-83,3=2352 ~2,35 103 kW.
Calculer
la puissance perdue par effet Joule au rotor PJR.
PJR = g Ptr
= 0,04*2,35 103
~94 kW.
Bilan de puissances.
Calculer
la puissance utile du moteur Pu.
Pu = Ptr -PJR
- Pm =2,35 103-94-87,2
=2168 ~2,17 103 kW.
En déduire
son rendement η.
n
= Pu */ Pa = 2168 / 2500
=0,866 ~0,87 ( 87 %).
Calculer
le moment du couple utile Tu.
w
= 2 p nn/60
= 2*3,14 * 1440/ 60 =150,7 rad/s ; Tu = Pu
/ w =2,17
103 / 150,7 ~14,4 N m.
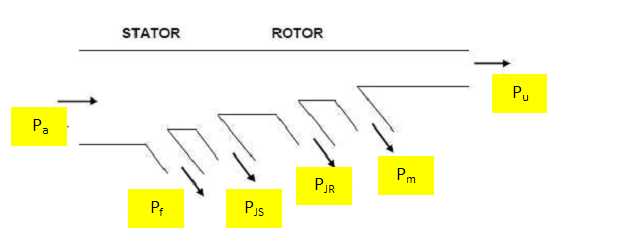
Compléter
le bilan de puissances en précisant les puissances mises en jeu.
|
.
Les
cannes défibrées sont acheminées aux moulins par un tapis roulant. La
masse de canne acheminée en une heure a pour valeur 375 tonnes et on
considère ce débit constant. La vitesse du tapis vaut v = 7,2 km.h-1.
La distance à parcourir est D = 10 m et le tapis est incliné d'un angle
de 11° par rapport à l'horizontale selon le schéma ci dessous.
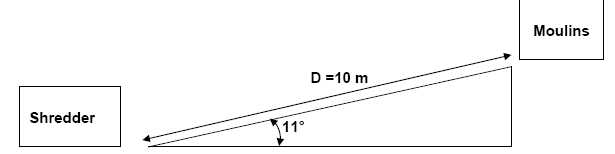
On donne : g = 9.81 N.kg-1.
Calculer
la durée d'acheminement de la canne entre le shredder et les moulins, Δt.
Dt =
D / v avec v = 7,2 / 3,6 = 2,0 m/s ; Dt = 10 / 2,0 =
5,0 s.
Déterminer
la masse de canne défibrée transportée pendant cette durée.
Débit : 375/3600 =0,104 t s-1 ; m =
0,104*5 =0,5208 t = 520 kg.
Calculer
le poids correspondant à cette masse, P.
P = m g = 520,8 *9,81 =5,1 103 N.
On suppose que le travail mécanique WU que doit
produire le moteur qui entraîne le tapis correspond au travail du poids
des cannes transportées entre le shredder et les moulins. Montrer
qu’il est égal à 9,75 kJ.
WU = mgD sin 11 = 520,8*9,81*10*sin 11 =9,75 103
kJ.
Calculer
la puissance utile de ce moteur, Pu.
Pu = WU / Dt = 9,75
103 / 5 = 1,95
kW.
Installation
triphasée.
Les caractéristiques électriques des
trois types de moteurs asynchrones triphasés utilisés dans cette
installation sont regroupées dans le tableau ci-dessous.
|
Nombre
de moteurs |
Puissance
absorbée par moteur (kW) |
Facteur
de puissance |
| Shredder |
1 |
Pas
= 2500 |
ks
= 0,80 |
| Moulin |
5 |
Pam
= 700 |
km
=0,75 |
| Tapis |
1 |
Pac
=2,50 |
kc
= 0,85 |
L'installation est alimentée par un
réseau triphasé 4300 V / 7500 V ; 50 Hz.
Calculer
la puissance active totale de l'installation, Pt, la puissance réactive totale de
l'installation, Qt, la
puissance apparente de l'installation, St.
Pt = Pas + 5 Pam +Pac =2500+5*700+2,50 =6,0 103
kW.
fas
=cos-1(0,80) =36,8 ; sin 36,8 =0,60 ; Sas
= Pas / ks ; Qas
=0,6 Pas
/ ks =06*2500/0,8 = 1,875 103
kvar.
fam
=cos-1(0,75) =41,4 ; sin 41,4 =0,661 ; Sam
= 5Pam / km ; Qam
=0,661 *5 Pam
/ km =0,661*5*700/0,75 = 3,085 103
kvar.
fac
=cos-1(0,85) =31,79 ; sin 31,79 =0,527
; Sac = Pac
/ kc ; Qac
=0,527
Pac / kc =0,527*2,5/0,85
= 1,55 kvar.
Qt = Qas +Qam +Qac =1,875 103
+3,085 103
+1,55 =4,96 103 kvar.
St = (Pt2
+Qt2)½
=((6,0 103)2 +(4,96 103)2)½
=7,78 103 kVA.
Déterminer
l'intensité du courant I qui traverse les lignes de l’installation.
I = St /(3½U) =7,78 103
/ (1,732*7500) =0,60 kA = 6,0 102 A.
Déterminer
le facteur de puissance global de l’installation k. Commenter la valeur
obtenue.
k = Pt / St =6,0 103
/ (7,78 103) =0,77. Cette valeur est trop
faible, elle doit être supérieure ou égale à 0,90.
Comment
doit-on procéder pour améliorer cette valeur ?
Brancher à l'entrée de
l'installation une batterie de condensateurs.
Le sirop est chauffé dans les
chaudières de la température initiale θi = 30 °C
à la température finale θf = 55 °C.
En une journée, les chaudières fonctionnent pendant huit heures et
traitent une masse m = 375 tonnes de sirop.
Données
: chaleur massique du sirop : c = 4,18 kJ.kg-1.K-1.
Relation : Q = m.c.Δθ
Calculer
la quantité de chaleur Q nécessaire au chauffage du sirop traité
quotidiennement.
Q = 375 103*4,18 (55-30) =3,92 107
kJ.
En
déduire la puissance P des chaudières.
P = Q / durée (s) = 3,92 107 /
(8*3600) =1,36 103 kW.
|
-
|
|



