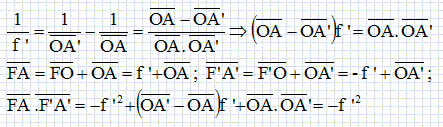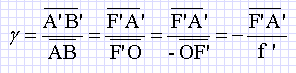Appareil photographique, profondeur de champ : concours Mines  2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

La bille effectue des oscillations sinusoïdales d’amplitude A voisine de 10 cm à une fréquence proche de f = 1 Hz. On veut photographier l’ensemble du dispositif expérimental (de hauteur totale h = 1 m). On utilise un objectif photographique assimilable à une lentille mince convergente de distance focale image f’ = 50 mm. L’image est enregistrée sur une pellicule notée Π de dimensions 50 mm* 50 mm. A quelle distance mettre l'apareil photo ?  Pour une lentille convergente de centre O, construire l’image A’B’ d’un objet réel AB perpendiculaire à l’axe optique, A appartenant à l’axe optique, placé avant le foyer objet F. 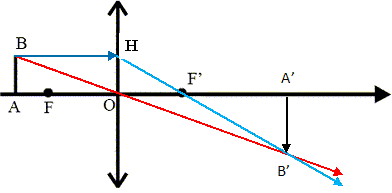 Utiliser cette construction pour démontrer la relation de conjugaison de Newton 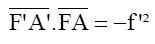 d’une lentille mince et l’expression du grandissement transversal γ : 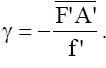Les triangles A'B'F' et OHF' sont semblables.     A quelle distance minimale de F peut-on mettre le dispositif expérimental pour le voir entièrement sur la pellicule ? Hauteur de l'objet h = 1,0 m ; hauteur maximale de l'image 0,050 m. Grandissement transversal g = -0,050/1,0 = -0,050. 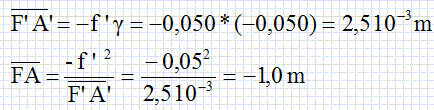L'appareil doit se situer au moins à 1,05 m du dispositif. Quel diaphragme utiliser ? Pour obtenir une photo bien nette, sur laquelle la bille apparaît figée, on estime que la bille ne doit pas se déplacer de plus de d = 1 mm pendant la durée de la prise de vue τ. D’autre part, la quantité totale de photons atteignant la pellicule doit être à peu près constante pour obtenir une photo ni sous-exposée (sombre car pas assez de photons pour impressionner la pellicule) ni surexposée (blanchie par un excès de photons). Pour pouvoir remplir cette condition à plusieurs durées de prise de vue τ, on accole un diaphragme à l’objectif. Le diamètre D du diaphragme est réglable afin de laisser entrer plus ou moins de lumière suivant l’intensité de l’éclairage et la durée de la prise de vue τ. Pour l’objectif (de distance focale image f’ = 50 mm) et la pellicule utilisés, on doit choisir D = 10 mm pour une durée de prise de vue de τ = 4.10-3 s dans les conditions d’éclairage de l’expérience. Calculer la vitesse maximale de la bille. vmax = d  / t =  1 10-3 / 4 10-3 = 0,25 ~ 0,3 m/s.  Estimer la durée maximale τmax de la prise de vue pour avoir une photo nette, sans flou de bougé en fonction de d, ω et A (ω est la pulsation des oscillations). Faire l’application numérique. z = A sin (wt) ; z' = v = Aw cos (wt) ; vmax = Aw = d /τmax ;  τmax = d / (Aw). τmax = 10-3 / (0,1 *2*p*1) ~0,01 / 6 ~1,7 10-3 s.  Justifier que la quantité de photons atteignant la pellicule est proportionnelle à τ et D2. En déduire le diamètre D du diaphragme qu’il faut alors utiliser pour obtenir une photo sans flou de bougé. La quantité de photons atteignant la pellicule est proportionnelle à la surface ( p D2) de l'ouverturedu diaphragme et à la durée de l'ouverture du diaphragme. D2 t =   0,0102*4.10-3 = 4.10-7 ; D'2 τmax =4.10-7 ; D'2  =4.10-7 / 1,66 10-3 = 4.10-4 / 1,6 ~2,5 10-4 ; D' = 0,016 m. Profondeur de champ. La profondeur de champ est l’intervalle de valeurs de la distance OA sur lequel les images peuvent être considérées comme nettes sur la pellicule Π. Les grains de la pellicule ont un diamètre a = 10 μm donc les images les plus petites ont un diamètre a = 10 μm (petite tache et non un point). Le dispositif photographié est à la distance 1 m de l’objectif. Sur la figure en annexe, la pellicule est dans le plan de l’image A’ d’un objet A à 1 m du foyer F de l’objectif. La distance focale de l’objectif est toujours f’ = 50 mm mais l’échelle n’est pas respectée afin que la construction soit lisible. Le diaphragme a pour diamètre D = 15 mm. On a tracé le rayon incident A1I le plus incliné par rapport à l’axe optique où A1 est un objet sur l’axe optique différent de A. Tracer la marche du rayon A1I après l’objectif.  L’image A’1 de A1 sur la pellicule n’est pas un point mais une tache de rayon r. En utilisant le théorème de Thalès (ou toute autre méthode), donner r en fonction de D, OA1’ et A’A1’. 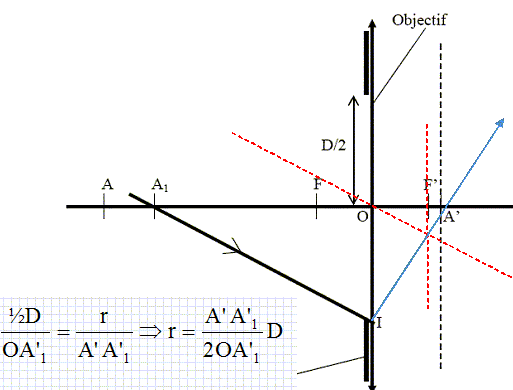 En déduire la valeur numérique maximale acceptable de A’A1’ pour que l’image de A1 soit vue nette sur la photo. OA' ~ f '. rmax = 10 10-6 m ; A'A'1max = 2 rmax OA'1 / D =2 10-5 *5 10-2 / 1,5 10-2 =6,66 10-5 ~ 7 10-5 m. Cette valeur permet ensuite de remonter à la valeur maximale de AA1. On trouve (calcul non demandé) AA1 < 2,3 cm. Cela convient-il pour photographier le dispositif ? Diamètre de la bille d ; section du tube s = p d2/4  = 2 cm2 ;  d ~( 8 / 3)½ ~ 1,6 cm Cette valeur étant inférieure à 2,3 cm, l'image de la bille sera nette. .

menu