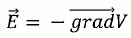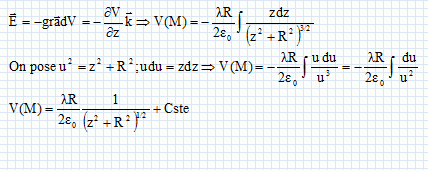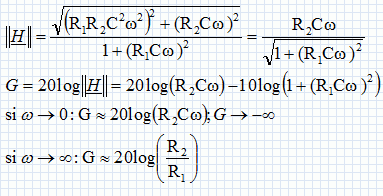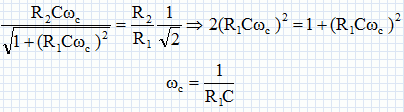Effet Doppler, champ d'une spire circulaire, filtre actif passe haut : concours ITPE 2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

Effet Doppler : Un objet mobile appelé cible noté M, se déplace avec une vitesse uniforme v le long d'un axe Oz. Au point O se trouve un dispositif qui permet d'envoyer des impulsions, très brèves, à une fréquence donnée et de détecter le signal renvoyé par la cible. On note c la vitesse de  ces impulsions dans le milieu considéré. Cette vitesse n'est pas modifiée par la cible. Les impulsions sont considérées comme une suite de bips émis à la fréquence f ( on note T la durée entre deux bips ). Le but de cette question est de déterminer la fréquence du signal détecté après réflexion sur la cible. A l'instant t1, l'émetteur émet un bip qui se dirige vers la cible. Celle-ci reçoit la signal alors qu'elle se trouve au point de côte z1. Exprimer l'instant t'1 auquel la cible reçoit la bip en fonction de t1, z1 et c. On compte positive, les vitesses dans le sens du signal. En t'1, le bip parcourt la distance ct'1 et se trouve au point de côte z1 = ct'1 ; t'1 = t1 + z1 / c. A l'instant t2 = t1+T l'émetteur émet un nouveau bip qui se dirige vers la cible. Celle-ci reçoit la signal alors qu'elle se trouve au point de côte z2. Exprimer l'instant t'2 auquel la cible reçoit la bip en fonction de t2, z2 et c. En t'2, le bip parcourt la distance ct'2 et se trouve au point de côte z2 = ct'2 ; t'2 = t2 + z2 / c. Exprimer la durée T ' = t'2-t'1 en fonction de T, z1, z2 et c. T ' = t2 + z2 / c -t1 - z1 / c = T+ z2 / c- z1 / c= T +(z2-z1) / c. Exprimer l'écart z2-z1 en fonction de v et T '. En déduire l'expression de T ' en fonction de T. Interpréter ce nouveau résultat. z2-z1 = v T ' = c(T '-T ) ; T ' ( c-v) = cT ; T ' = c / (c-v) T = 1 / (1-v/c) T. T ' est supérieur à T. En déduire la fréquence f' du signal au niveau de la cible en mouvement.  f ' = 1 / T ' = (1-v/c)  / T. On suppose que la cible renvoie instantanément le bip qui possède la fréquence f '. Par un raisonnement analogue, montrer que les bips détectés en O après réflexion sur la cible ont une fréquence 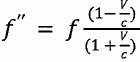 . Le récepteur reçoit le premier bip à l'instant t"1 =t'1 + z1 / c et le second bip à l'insatnt t"2 = t'2 + z2 / c. T" = t"2- t"1=t'2 + z2 / c-t'1 - z1 / c = T ' +(z2-z1) / c ; or z2-z1 = v T '. T" = T ' +v/ c T '= (1+v/c) T ' =(1+v/c) / (1-v/c) T. f " = 1 / T " = (1-v/c) / (1+v/c) f. Dans le cas où v << c : 1 / (1+v/c) ~ 1-v/c et  (1-v/c) / (1+v/c) ~ (1-v/c)(1-v/c) = (1-v/c)2. (1-v/c)2~1-2v/c. Par suite f " ~ f (1-2v/c). Dans les conditions précédentes, un cinémomètre émet des bips à la fréquence f0 = 1,00 GHz ; on mesure un écart |f "-f0| = 2,05 Hz. Déterminer la vitesse de l'avion visé. ( c = 3,00 108 m/s). 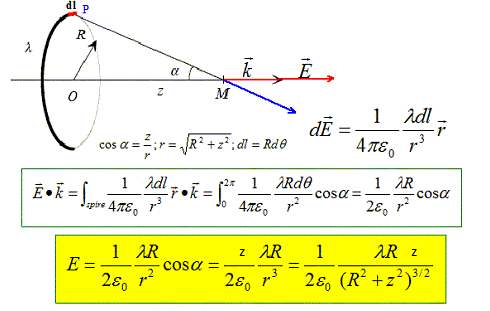|f "-f0| ~2v f0 /c ; v ~|f "-f0| c / (2f0 ) = 2,05 *3,00 108 / 2,00 109 =0,3075 ~0,308 m/s.   Champ électrique crée sur l'axe d'une spire circulaire. On considère une spire circulaire de centre O et de rayon R. Cette spire porte une charge électrique de densité linéïque l supposée positive. On note e0 la permitivité du vide. On note z la coordonnée du point M sur l'axe de la spire. Par des considérations qualitatives précises, déterminer la direction du champ électrique en M..   Déterminer  E. k est un vecteur unitaire porte par l'axe Oz.  Tout plan défini par le point M et un diamètre de la spire ne modifie par la distribution de la charge : E appartient à l'intersection de tous ces plans, c'est à dire que E est porté par l'axe Oz. Dans une symétrie par raport au plan contenant la spire, z devient -z : donc E(-z) = -E(z). Tracer l'allure de la fonction E(z). Détermination du potentiel électrostatique. Donner la signification du signe moins dans où V représente le potentiel électrostatique. Le sens du champ électrique est dirigé dans le sens des potentiels décroissants. Etablir l'expression de V(M) en fonction de z et des données.Tracer l'allure de V(z). Le potentiel est choisi nul à l'infini : dans ce cas la constante d'intégration est nulle. On place en M une charge q astreinte à se déplacer uniquement sur l'axe Oz. Exprimer l'énergie potentielle de la charge q. 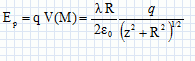Déterminer la position d'équilibre de la charge q. A quelle condition cette position d'équilibre est-elle stable ? A une position d'équilibre, l'énergie potentielle est minimale : sa dérivée par rapport à z est nulle. 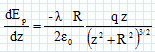Le point z=0 est une position d'équilibre. Cette position d'équilibre est stable, si en écartant la charge de cette position, elle est soumise à une force de rappel vers z=0. Ecartée de cette position d'équilibre, la charge est soumise à la force 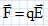. 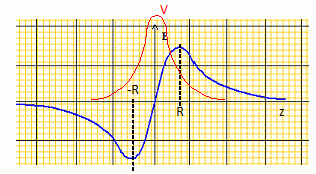Le champ étant dirigé dans le sens de l'axe, pour z >0, la force sera dirigée vers z=0 si la charge q est négative. Tracer la courbe représentative de l'énergie potentielle et retrouver les résultats précédents. 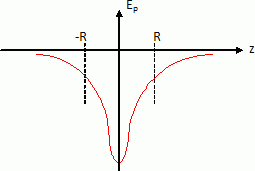On observe bien un puits de potentiel au point z = 0. On souhaite étudier le mouvement de la charge autour de sa position d'équilibre. Etablir l'équation différentielle du mouvement dans l'hypothèse des faibles amplitudes. Le poids de la charge est négligeable devant la force électrique 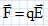. Ecrire la seconde loi de Newton suivant l'axe z. 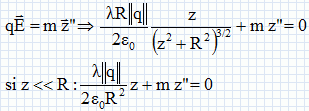Quelle est la nature du mouvement ? Donner une caractéristique de ce mouvement. On retrouve l'équation différentielle d'un oscillateur harmonique : le mouvement est sinusoïdal périodique. Electronique. On considère le montage ci-dessous alimenté par une tension sinusoïdale u(t) = Ue0 sin (wt). L'A.O est idéal et fonctionne en régime linéaire. Exprimer la tension de transfert H = Vs/ Ve. On note i l'intensité traversant R1 et R2. Vs= -R2 i ; i =- Vs/R2. Ve = (R1 + 1/ (jCw) i ; i  = Ve jCw / (R1Cjw + 1). - Vs/R2 = Ve jCw / (R1Cjw + 1). H = - R2Cjw / (R1Cjw + 1) = - R2Cjw  ( 1-R1Cjw ) / (1+(R1Cw)2). H = -(R1R2C2w2+R2Cjw )/ (1+(R1Cw)2). Exprimer le gain en tension , en décibel, G du montage. Il s'agit d'un filtre passe haut. Déterminer la pusation de coupure à une atténuation du gain de 3 dB. Hmax =R2 / R1 ; à la fréquence de coupure H =Hmax / 2-½. Donner l'allure de la courbe G(log w).

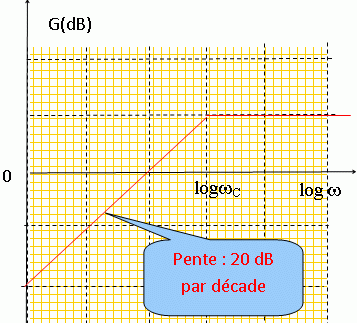
A.N : R2 = 10 kW; Gmax = 40 dB ; fc = 1500 Hz. Hmax = R2 / R1 ; R1  = R2 / Hmax avec Hmax = 10Gmax/20 =100 ; R1  = 104 / 100 = 100 ohms. wc = 2 p fc =6,28*1500 = 9425 rad/s ; C = 1/(R1wc )= 1/(100*9425) =1,06 10-6 F. Exprimer le déphasage F de la tension de sortie par rapport à la tension d'entrée. Donner l'allure de la courbe F (logw). F = arg H = 1/(R1Cw) ;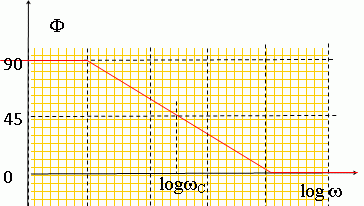

menu