Aurélie 01/05/11
 

 

   Emulsions : centrifugation fractionnée : concours général 2011.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
. .
.
.

Sédimentation.
On parle de sédimentation lorsque de petits objets tombent au fond d'un fluide.
Soit un grain sphérique, de volume Vg, de masse volumique µ, dans l'eau ( solvant de l'émulsion ), de masse volumique µeau qui remplit un tube à essai placé verticalement. O note a le coefficient de frottement visqueux dans l'eau. Ce coefficient dépend de la forme de l'objet et de la viscosité du fluide. Dans ce cas a = 6 p heau a. ( a : rayon du grain ).
Effectuer un bilan des forces appliquées à ce grain au cours de sa chute au sein du liquide.
Le grain est soumis à son poids, verticale, vers le bas, valeur mg = Vg µ g
à la poussée d'Archimède, verticale, vers le haut, valeur Vg µeau g
à la force de frottement visqueux, verticale, vers le haut, valeur : 6 p heau a v ( v : vitesse de chute du grain ).
Pourquoi la force de frottement visqueux est-elle ( en général ) négligeable dans l'air et pas dans l'eau ?
La viscosité de l'air est très inférieure à celle de l'eau.
On observe expérimentalement une vitesse limite de chute vlim du grain.
 Déterminer son expression.
Lorsque la vitesse limite est atteinte, la somme vectorielle des forces appliquées au grain est nulle.
Vg µ g = 6 p heau a vlim +Vg µeau g.
6 p heau a vlim = Vg µ g-Vg µeau g = Vg  g (µ -µeau )
vlim =Vg  g (µ -µeau ) / (6 p heau a). On note m* = Vg   (µ -µeau ) d'où : vlim =m*  g / (6 p heau a) = m*  g / a.


Interpréter qualitativement l'appellation " masse apparente". Que se passe t-il si m* < 0 ?
La différence entre le poids et la poussée d'Archimède est le poids apparent ( le poids de l'objet plongé dans un liquide, paraît plus faible ). A ce poids apparent, on associe une masse apparente. Si la masse apparente est négative, l'objet flotte à la surface du liquide.
Calculer la vitese limite pour les grains suivants  : heau = 1,0 10-3 Pa s ; g = 9,81 m s-2.
a ( µm )m* ( kg )a ( SI)vlim ( m/s )
a1 =1,0 m*1=8,126 10-161,88 10-84,24 10-7
a2 =0,5m*2=1,016 10-169,4 10-91,06 10-7
 

Justifier le facteur relatif ainsi obtenu entre vlim1 et vlim2, en exprimant le rapport vlim1 / vlim2 en fonction de a1 et a2 .
vlim1 = m*1  g/ a1. vlim2 = m*2  g/ a2. vlim1 / vlim2 =m*1a2 /( m*2 a1) = 8 a2/a1.
On vérifie : vlim1 / vlim2  = 4 ;  a2/a1  =0,5  ; vlim1 / vlim2  = 8 a2/a1  ;

En appliquant la seconde loi de Newton au système grai de masse m, montrer que l'équation différentielle du mouvement suivant un axe vertical descendant peut se mettre sous la forme : dv/dt +v/t = m*/m g.
Vg µ g -Vg µeau g-6 p heau a v = mdv/dt ; Vg  g (µ- µeau )-6 p heau a v = mdv/dt
m*g-a v = mdv/dt ; dv/dt +a/m v = m*/m g. On pose t = m/a.
On constate que le grain de rayon a1 = 1,0 µm et de masse m1 = 5,0 10-15 kg atteint immédiatement sa vitesse limite. Justifier.
t1 = m1 / a1 avec a1 =1,88 10-8 ; t1 =5,0 10-15 / 1,88 10-8  =2,66 10-7 s.
La vitesse limite est atteinte au bout d'une durée supérieure ou égale à 5 t1 soit 5*2,66 10-7 =1,3 10-6 s = 1,3 µs.
En déduire la durée Dt1, mise par le grain de masse apparente m*1 pour atteindre le fond du tube de hauteur h = 10 cm.
Dt1 = h / vlim1  = 0,10 /4,24 10-7 =2,36 105 s ~65,5 heures.
On rappelle qu'on cherche à sélectionner les sphères de même taille. Commenter ce résultat. Pour une émulsion donnée, quel paramètre faut-il modifier ?
Même en divisant la hauteur de chute par deux ou par trois, la durée mise par le grain pour atteindre le fond du tube est bien trop grande.


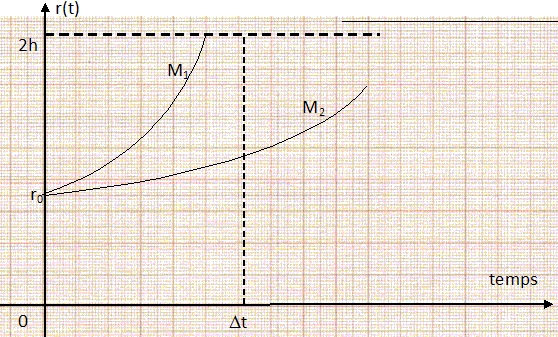
Centrifugation.
Une fois l'émulsion obtenue, on la soumet à une centrifugation énergique ( comme on fait pour séparer les globules rouges du sang ). En utilisant des vitesses de rotation de l'ordre de 2500 tours / minute, cela donne à 15 cm de l'axe une force centrifuge 1000 fois supérieure à la pesanteur.
Quelle est l'intérêt d'une " pesanteur 1000 fois plus grande" ?
   La vitesse limite de chute est proportionnelle à g ; la vitesse limite sera 1000 fois plus grande ( et la durée de la séparaton 1000 fois plus petite) si la pesanteur est multipliée par 1000.
Analysons maintenant comment J Perrin a pu séparer les gros grains des plus petits jusqu'à obtenir une émulsion uniforme. Pour cela on considère 2 grains M1 et M2 de taille différentes ( rayons a1 et a2) et donc de masses m1 et m2 différentes avec m1 > m2. On suppose qu'initialement ils se trouvent à la même distance r0 de l'axe.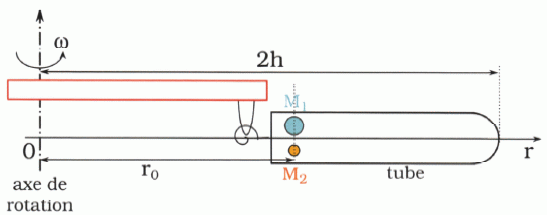

 On leur fait subir une centrifugation fractionnée au moyen d'une centrifugeuse. En rotation, les tubes remplis d'émulsion, se trouvent à l'horizontale ; la distance entre l'axe de rotation et le fond du tube est toujours 2h.
On se place dans le référentiel lié au tube ( ce référentiel tourne à la vitesse angulaire w dans le référentiel terrestre, supposé galiléen ). Dans ce référentiel non galiléen, les grains sont sensibles à la force centrifuge qui s'exerce dans le sens de la longueur du tube :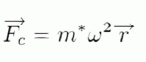
r est un vecteur donnant la distance du grain à l'axe de rotation, orienté de l'axe vers le fond du tube ; m* est la masse apparente  du grain ; w s'exprime en rad/s.
Lors de centrifugation de courte durée, cette force s'oppose à la force de frottement fluide ou visqueux  qu'exerce le solvant sur le grain.
Calculer la vitesse angulaire w du rotor ( en rad/s) utilisé par J. Perrin.
2500 tours/min = 2500/60 tr/s =41,67 tr/s ; w = 41,67 *2*3,14 =261,8 rad/s.
Représenter les forces horizontales s'exerçant sur les particules M1 et M2 dans le plan de la figure.
On suppose que le mouvement d'un grain est unidirectionnel et on note sa vitesse instantanée v = dr/dt.
Appliquer la seconde loi de Newton à cette particule en fonction de a, m*, m, w, r, dr/dt et dv/dt.
On admet que l'accélération dv/dt est négligeable ; en déduire l'équation différentiele donnant la distance r(t).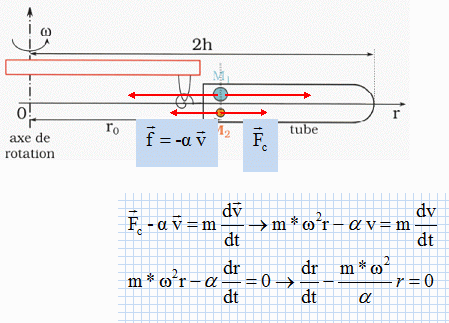
Montrer que la position r(t) d'un grain au cours du temps s'écrit : r(t) = A exp(+ßt) où ß est une constante que l'on exprimera en fonction de m*, a et w.
On pose ß =m*w2/a ; dr/dt -ßr = 0 ; r(t) = A exp(+ßt).
A t=0, r(t=0) = A = r0, distance initiale du grain à l'axe.




Tracer l'allure des courbes associées aux fonctions r(t) pour les grains M1 et M2.
m1* = 8 m2* ; a1= 2 a2 ; ß =m*w2/a ; ß1 = 4 ß2.
r1(t) = r0 exp(+ß1t) ; r2(t) = r0 exp(+ß1/ 4t).


On arrête la centrifugation au bout de Dt.
Montrer que cela permet de séparer les grains en fonction de leur taille.
Les grains de masse égale ou supérieure à m1 sont rassemblés au fond du tube et constituent une "boue".
Les grains de masse égale ou inférieure à m2 sont encore en solution " liquide impur au dessus de la boue".
On décante le liquide impur ; on remet dans l'éprouvette de l'eau distillée jusqu'à la hauteur primitive ; on agite avec la boue, dont tous les grains se séparent et on recommence l'opération précédente avec la même vitesse angulaire et la même durée de centrifugation. On décante l'émulsion qui surmonte le second sédiment, plus pâle que la remière fraction décantée, et on recommence les opérations jusqu'à ce que le liquide qui se trouve au dessus du sédiment à la fin de chaque centrifugation devienne presque de l'eau claire. " Annales de chimie et de physique Jean Perrin 8è série tome XVIII sept 01909."
Calculer la valeur de Dt qui permet de placer les grains les plus gros ( M1) au fond du tube de hauteur totale h = 10 cm.
On prendra r0 = 11 cm  puis r0 = 19 cm ; heau = 1,0 10-3 Pa s. Force centrifuge 500 fois plus grande que la pesanteur. 30 tours / seconde.( w = 2*3,14 *30= 188,5 rad/s )
ß =m1*w2/a1 =8,126 10-16 *188,52 /1,88 10-8 =1,536 10-3 s-1.
r(Dt) = h +r0 = 0,10 +0,11 = 0,11 exp( 1,536 10-3 Dt) ; ln(0,21/0,11) = 1,536 10-3 Dt ;
Dt =4,2 102 s ~7,0 min.
r(Dt) = h +r0 = 0,10 +0,19 = 0,19 exp( 1,536 10-3 Dt) ; ln(0,29/0,19) = 1,536 10-3 Dt ;
Dt =2,75 102 s ~4,6 min.
Dans les deux cas à quelle distance de l'axe se trouve le grain le plus petit M2 ?
r(Dt) = r0 exp(+ß1/ 4Dt) = 0,11 exp(1,536 10-3 / 4 *4,2 102) =0,13 m
Ce grain est à 13 cm de l'axe ; le fond du tube est à 21 cm  de l'axe ; ce grain est en solution.
r(Dt) = r0 exp(+ß1/ 4Dt) = 0,19 exp(1,536 10-3 / 4 *2,75 102) =0,21 m.
Ce grain est à 21 cm de l'axe ; le fond du tube est à 29 cm  de l'axe ; ce grain est en solution.


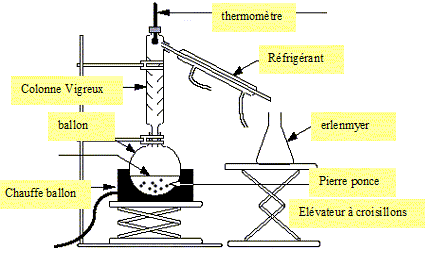
Selon J.Perrin, ce procédé peut se comprer à la distillation fractionnée.
Rappeler le principe de cette dernière et nommer le matériel utilisé au laboratoire.

La distillation fractionnée permet de séparer les constituants d'un mélange liquide- liquide miscibles, possédant des températures d'ébullition différentes.
Le constituant le plus volatil distille en premier ; la séparation est d'autant plus facile que les températures d'ébullition sont différentes.
Quelle(s) analogie(s) peut-on effectivement y voir ?
Aux températures d'ébullition différentes correspondent les masses différentes des grains.
Au composé le plus volatil correspond le grain le plus massif. 
Au mélange liquide-liquide miscibles correspond l'émulsion homogène.
Aux pointes de la colonne de Vigreux ( ou aux plateaux théoriques ) correspondent " On décante le liquide impur ; on remet dans l'éprouvette de l'eau distillée jusqu'à la hauteur primitive ; on agite avec la boue, dont tous les grains se séparent et on recommence l'opération précédente".

menu