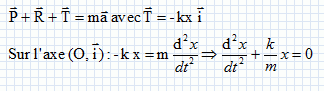Oscillations mécaniques et électriques : concours audioprothésiste Nancy 2009. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

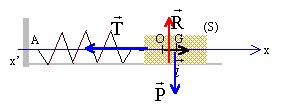
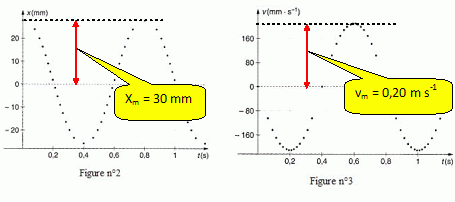
Oscillations mécaniques. Un oscillateur est matérialisé par un mobile autoporteur de masse m = 50,5 g assimilé à une masse ponctuelle ramenée au centre d’inertie G et liée à un ressort de masse négligeable. On négligera toutes forces de frottement. Sur l’axe des x, l’allongement du ressort est nul à l’origine x = 0 (position d’équilibre). On tire le mobile vers la droite d’une longueur x=x0=27mm, puis on le lâche sans vitesse initiale. 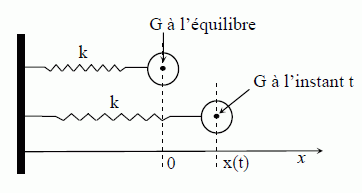A l’aide d’un dispositif non décrit ici, on enregistre l’élongation x (en mm) représenté sur la figure n°2, et la vitesse v (en mm.s-1) représentée sur la figure n°3. 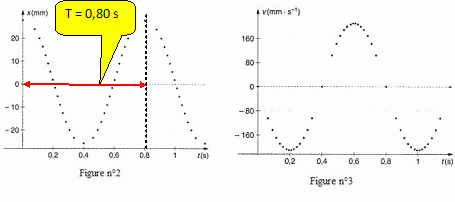Quel est la nature du régime d’oscillation ? Justifier. Les oscillations sont liubres sinusoïdales, périodiques et non amorties : l'amplitude de diminue pas au cours du temps. A l’aide du graphe de la figure n°2, déterminer la valeur de la période propre T de l’oscillateur. Après avoir fait le bilan des forces, montrer que l’équation différentielle caractéristique du mouvement de G est : d2x/dt2 +k/m x = 0 avec k : la constante de raideur du ressort Le solide S est soumis à  : son poids, vertical, vers le bas, valeur mg - à l'action du rail, vertical, vers le haut, valeur mg - à une force de rappel exercée par le ressort, proportionnelle à l'allongement. On donne une solution à cette équation : x(t)=  Xm cos(2p/T t +F). En déduire la valeur de la constante de raideur. x'(t) = -Xm 2p/T sin(2p/T t +F). x"(t) =-Xm (2p/T )2 cos(2p/T t +F) = -(2p/T )2 x(t) ; repport dans l'équation différentielle : -(2p/T )2 x(t) +k/m=0 soit : (2p/T )2 = k/m ou k = m (2p/T )2; k = 0,0505(6,28 / 0,80 )2= 3,1 N m-1. A l’aide des figures n°2 et n°3, trouver les valeurs de Xm et de ϕ. Donner la relation numérique de x(t) puis de v(t) à tout instant t. x(t=0)=  Xm  = Xmcos(F) ; cos(F) = 1 ; F =0 ; x(t)=  3,0 10-2 cos(6,28/0,8 t ) = 3,0 10-2 cos(7,85 t ). x'(t) =v(t) = -Xm 2p/T sin(2p/T t +F). v(t) = -0,24 sin(7,85 t ). Compléter le tableau et conclure sur la valeur de l'énergie mécanique. t(s) 0 0,25T 0,5 ½T x(m) 0,030 0 -0,020 -0,030 énergie potentielle (J) Ep= ½kx2 0,5*3,1*0,032 =1,410-3 0 6,2 10-4 1,4 10-3 vitesse ( m /s) 0 -0,24 0,17 0 énergie cinétique ( J) Ec=½mv2 0 0,5*0,0505*0,242 =1,4 10-3 7,3 10-4 0 énergie mécanique ( J)= Ec+Ep 1,410-3 1,4 10-3 1,35 10-3 ~1,4 10-3 1,4 10-3 Circuit électrique. On donne L = 10 mH, C = 100 nF, R = 100 ohms, E = 10 V. La résistance de la bobine est supposée nulle. 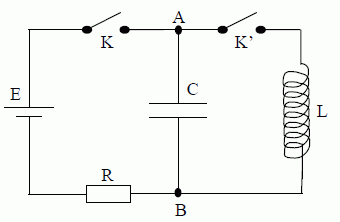Etude du régime permanent continu. En régime continu, les grandeurs électriques sont indépendantes du temps.  L’interrupteur K est fermé, K’ est ouvert. Le régime permanent est établi. Que peut-on dire de l’intensité qui traverse le condensateur ? de l’intensité qui traverse la résistance ? Le condensateur chargé se comporte, en courant continu, comme un interrupteur ouvert. L'intensité traversant le condensateur et la résistance R est donc nulle. Le condensateur est à nouveau déchargé. On ferme K et K’. Le régime permanent s’établit.  Montrer que la tension UAB aux bornes de la bobine est alors nulle. uAB = Ldi/dt ; en régime permanent l'intensité est constante et vaut I. Par suite dI/dt=0 et uAB = 0. En déduire la charge QA du condensateur. QA= uAB / C = 0. Déterminer l’intensité qui traverse la bobine et l’énergie emmagasinée par la bobine. La bobine se comporte comme un interrupteur fermé : additivité des tensions E = uAB + RI ; E = RI : I = E/R = 10/100 = 0,10 A. Energie stockée par la bobine : ½LI2 = 0,5*0,01*0,12 =5,0 10-5 J. Etude en régime oscillatoire. On ouvre l’interrupteur K à l’instant t = 0 s pris comme origine des temps. A t = 0 s, le condensateur est déchargé, l’intensité du courant i = -I0 = -0,1 A.  Montrer que le circuit équivaut au circuit représenté ci-dessous. Expliquer pourquoi, bien que le condensateur soit initialement déchargé, un courant d’intensité i variable va circuler dans le circuit. 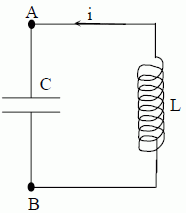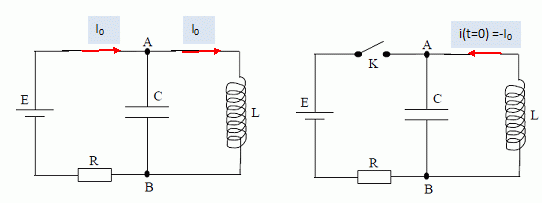La partie gauche du circuit se comporte comme un interrupteur ouvert. La bobine, stockant initialement toute l'énergie du dipôle LC, échange de l'énergie avec le condensateur. La continuité de l'intensité traversant la bobine conduit à i(t=0) = I0 = i(t=0+)= 0,1 A. On choisit une autre orientation de parcours du circuit, d'où le signe négatif pour l'intensité initiale. Etablir l’équation différentielle vérifiée par la charge q(t) du condensateur. la charge de l'armature A du condensateur est notée q. uAB = q/ C  = -Ldi/dt avec i = dq /dt et di/dt = d2q/dt2. q / C  +Ldi/dt  =0 ; Ld2q/dt2 + q / C = 0 ; q" +1/(LC) q = 0. Sachant que la solution à cette équation différentielle est de la forme q(t)=  Q cos(2p/T t +F), déterminer complètement l’expression des fonctions q(t) et i(t). Lorsque le condensateur stocke toute l'énergie du dipôle : ½Q2/C = ½LI02 ; Q = (LC)½I0 = (10-2*10-7)½*0,1 =3,16 10-6 C ~3,2 10-6 C. A t=0, le condensateur est déchargé q(t=0) = 0 = Q cos(F) d'où F = ½p ou -½p. T = 2 p(LC)½ ; 2p/T = 1/LC)½ = 1/(10-2*10-7)½ =3,16 104 ~3,2 104 rad/s. q(t) = 3,2 10-6 cos (3,2 104 t +½p) ou q(t) = 3,2 10-6 cos (3,2 104 t -½p). i(t) = dq/dt = -Q 2p/T sin(2p/T t +F) ; i(t=0) = -0,1 = -Q 2p/T sin(F). Q 2p/T étant positif, sin(F) = 1 et  F = ½p. q(t) = 3,2 10-6 cos (3,2 104 t+ ½p) et i(t) = - 0,1 sin (3,2 104 t +½p). q(t) = 3,2 10-6 sin (3,2 104 t ). En réalité, la résistance de la bobine n’est pas négligeable, mais faible. Donner l’allure de la courbe représentative de i(t).

menu