Echographie ; effet Doppler : DTS IMRT 2011. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

. .

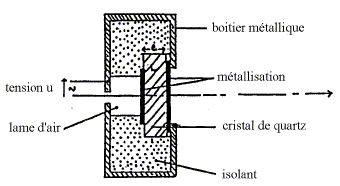
Ultrasons. Quelle est la nature des ondes sonores ? Peuvent-elles se propager dans le vide ? Les onde sonores sont des ondes mécaniques progressives longitudinales ; une onde mécanique nécessite un milieu de propagation. ( elles ne se propagent pas dans le vide ). A partir de quelle fréquence peut-on qualifier les ondes d'ultrasonores ?  Le domaine des ultrasons commence à des fréquences supérieures ou égales à 20 kHz.(20 kHz à 1 GHz.)  Nommer et expliquer brièvement le phénomène qui permet de générer des ultrasons. La piézoélectricité découverte par Pierre et Jacques Curie, peut être mise en évidence avec certains cristaux anisotropes, comme le quartz. Pour une échotomographie abdominale, on utilise un émetteur à ultrasons, constitué d'une lame de quartz (L) dont les faces parallèles ont été métalisées. Elle vibre sous l'action d'un champ électrique alternatif obtenu en appliquant entre les deux faces parallèles de la lame une tension sinusoïdale u, de fréquence f = 3,75 MHz. Impédance acoustique. L'impédance acoustique Z d'un milieu est donnée par la relation Z = r c où r est la masse volumique du milieu et c la célérité du son dans ce même milieu. Calculer l'impédance acoustique de chacun des trois milieux : air, peau et graisse, os. air : r = 1,3 kg m-3 ; c = 3,4 102 m/s ; Zair =1,3 *3,4 102 =442 ~4,4 102 kg m-2 s-1. peau et graisse : r = 1,0 103 kg m-3 ; c = 1,4 103 m/s ; Zpeau =1,0 103 *1,4 103 =1,4 106 kg m-2 s-1. os : r = 1,9 103 kg m-3 ; c = 4,0 103 m/s ; Zpeau =1,9 103 *4,0 103 =7,6 106 kg m-2 s-1. 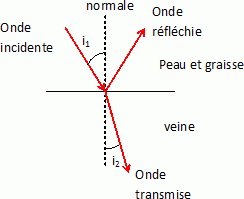Le coefficient de transmission en énergie pour le passage du son d'un milieu 1 vers un milieu 2, en incidence quasi- normale, est donné par l'expression : a = 4 Z1Z2 / (Z1+Z2)2. Calculer les coefficients de transmission en énergie pour les interfaces air-(peau et graisse) et (peau et graisse)-os. Conclure. Interface air-(peau et graisse) : a1 =4*442*1,4 106 / (442 +1,4 106)2 ~1,3 10-3. Interface (peau et graisse)- os : a2 =4*7,6 106*1,4 106 / (7,6 106 +1,4 106)2 ~0,53. Les ultrasons ne sont pratiquement pas transmis de l'air dans le milieu ( peau et graisse) ; les ultrasons sont assez bien transmis du milieu peau et graisse dans l'os. Comment améliorer l'interface air- (peau et graisse ) ? Le gel permet de remplacer l'interface air-peau (eau) par l'interface gel-tissus (eau) : les ondes sont ainsi mieux transmises. Echographie. La sonde fonctionne en mode pulsé. En écho au train d'onde T1, on relève deux signaux e0 et e1. L'écho e0 est provoqué par l'interface gel / (peau et graisse ) et l'écho e1 par l'interface peau graisse / os. Une durée Dt = 20,8 µs sépare les échos e0 et e1. Les célérités des signaux dans les différents milieux sont données. On note d la distance entre l'os et la surface de la peau. Exprimer littéralement en fonction de d la distance d' parcourue par le signal pour produire l'écho e1. Justifier. Le gel a pratiquement la même impédance acoustique que la peau et la graisse. La célérité des ultrasons dans le gel, la peau et la graisse est à peu près la même. Donc les distances parcourues sont proportionnelles aux durées correspondantes. 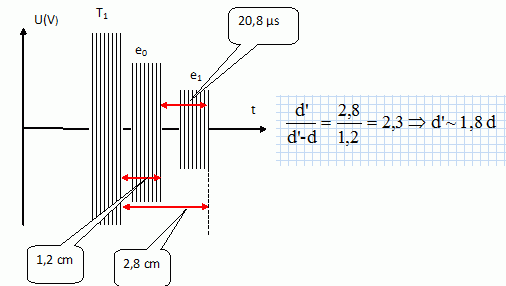Déterminer la relation entre d' et Dt puis en déduire la valeur de d. 2d = cpeau Dt ; or d = d'/1,8  ; 2d' =cpeau Dt *1,8 ; d' = 1,4 103 *1,8 / 2 Dt ~1,26 103 Dt. d = ½cpeau Dt  = 0,5 *1,4 103 *20,8 10-6 =1,5 10-2 m ~1,5 cm. Caractériser qualitativement les échos par rapport au train d'onde T1. La fréquence, caractéristique de l'onde, est identique pour T1 et les échos. Les ultrasons perdent de l'énergie en traversant les tissus : l'amplitude diminue d'autant plus que l'épaisseur traversée est plus grande. Le coefficient linéique d'absorption µ du milieu peau-graisse, à la fréquence utilisée, est de 12,2 m-1. Donner l'expression de l'intensité du signal I en fonction de l'intensité initiale I0 après traversée d'un milieu d'épaisseur x. I = I0 exp (-µL) I0 : flux incident ; I : flux sortant ; µ : coefficient d'atténuation linéique du milieu ; x : épaisseur du milieu traversé. Exprimer l'intensité I' du signal en fonction de l'intensité initiale I après un aller -retour dans le milieu peau-graisse d'une épaisseur x. En déduire le rapport I'/I pour x = 1,5 cm. I' = I0 exp(-2µx). I'/I0 = exp(-2µx) = exp(-12,2 *0,030) =0,69. En réalité le rapport I'/I0 est inférieur à la valeur précédente. Quel phénomène est à l'origine de cette perte ? Une partie du faisceau est réfléchi par l'interface milieu1 / milieu 2, une autre partie est transmise dans le second milieu. L'interface n'est pas toujours perpendiculaire à la direction du faisceau d'ultrasons : l'onde réfléchie ne repart pas vers la source. Si l'interface est de petite taille par rapport à la longueur d'onde, les ultrasons sont diffusés dans plusieurs directions. Quel est l'intérêt d'utiliser des salves d'ultrasons ? Une salve est détectée avant que la salve suivante soit émise. Cela permet de réaliser non pas une seule image mais un film et d'observer en direct le fonctionnement de l'organe. Effet Doppler. On souhaite mesurer le débit sanguin dans une veine en mettant à profit l'effet Doppler. La sonde fonctionne en mode pulsé à la fréquence f = 4,3 MHz. On se place dans le cas où l'épaisseur du milieu ( peau graisse ) est négligeable devant celle de la veine. La célérité des ultrasons dans le sang est c = 1,5 103 m/s. Définir succinctement l'effet Doppler. La fréquence reçue par un récepteur est différente de la fréquence émise par un émetteur quand émetteur et récepteur sont en mouvement relatif. L'effet Doppler est le décalage de fréquence entre la mesure à l'émission et la mesure à la réception lorsque l'émetteur et le récepteur sont en mouvement relatif. L'écart en fréquence est donné par la relation : fr-f0 = 2 v cos q / c f0. Définir tous les termes de cette relation. fr : fréquence ( Hz) de l'onde réfléchie ; f0 : fréquence (Hz) de l'onde incidente ; v : vitesse (m/s) du sang ; c : célerité ( m/s) des ultrasons ; q : angle formé entre les directions de la veine et le faisceau d'ultrasons Calculer la vitesse du sang pour fr-f0 =0,50 kHz et q = 60°. v =c(fr-f0 ) / (2f0 cos q ) = 1500*500 / (2*4,3 106 *cos60)=0,1744 ~0,17 m/s. Pour quelle valeur de q, cet écart serait théoriquement maximum ? Cette valeur est-elle réaliste en pratique ? Si q=0, cos q= 1 : en pratique il est impossible que le faisceau d'ultrasons ait la même direction que la veine. Les ondes ultrasonores sont déviées à l'interface de deux milieux : sin i1 / c1 = sin i2 / c2. Si i1 = 30 °, calculer i2. sin i2 =  c2 sin i1 / c1 =1,5 103 *sin 30 / 1,4 103=0,536 ; i2 =32,3 ~32°. Comparer les valeurs de i1 et i2. En déduire si le phénomène de réfraction est préjudiciable pour déterminer la vitesse du sang dans la veine. Les angles i1 et i2 sont à peu près identique ( à 6 % près ). La réfraction n'est donc pas préjudiciable pour déterminer la vitesse du sang.

menu