Les
murs d'une maison sont constitués de briques creuses ; du côté
extérieur, les briques sont reconvertes d'un enduit-ciment, et du côté
intérieur sont fixés des panneaux comportant un isolant et du plâtre
cartonné.
| matériau | enduit | briques | isolant | plâtre | | épaisseur e (cm) | 1,0 | 20 | 8,0 | 1,0 | | conductivité thermique l (W m-1K-1) | 1,25 | 0,50 | 0,040 | 0,33 |
Résistance thermique surfacique intérieure : rsi = 0,11 m2KW-1. Résistance thermique surfacique extérieure : rse = 0,06 m2KW-1.
Température intérieure : qi = 20°C ; température extérieure : qe = -10°C.
|
|
Calculer la résistance thermique R pour 1,00 m2 de surface de mur. En déduire le coefficient K dr transmission thermique de surface.
R = rsi + rse + e1 / lenduit
+e2 / lbriques + e3 / lisolant
+e4 / lplâtre ;
R = 0,11+0,06 +0,010 /1,25 +0,20 /0,50 + 0,080 /0,040 +0,01/0,33 =2,6083 ~2,6 m2
K W-1.
K = 1/R = 1/ 2,6083 =0,3834~ 0,38 W K-1 m-2.
Déterminer les températures de surface.
Flux thermique surfacique f =K(qi -qe) =0,3834(20+10) =11,5017 Wm-2.
f =1/rsi(qi -qi s) ; qi s=qi - f rsi =20-11,5017*0,11 = 18,7°C.
f =1/rse(qe s -qe) ; qe s=qe + f rse = -10+11,5017*0,0,6 =- 9,3°C.
Les caractéristiques des parois d'une maison sont les suivantes :
Parois
|
superficie (m2)
|
coefficient de transmission
thermique surfacique
W K-1 m-2
|
Si Ui
W K-1
|
murs sans isolation
|
S1 =72,8
|
U1 =1,10 |
80,08
|
vitrage simple
fenêtre, porte
|
S2 =12,7 |
U2 =5,00 |
63,5
|
plafonds sous combles
10 cm d'isolant
|
S3 =72,0 |
U3 =0,38 |
27,36
|
plancher sur vide sanitaire
|
S4 =72,0 |
U4 =0,91 |
65,52
|
|
Total :
|
236,46
|
Température intérieure : qi = 20°C ; température extérieure : qe = -10°C.
Donner l'expression littérale du flux thermique total F transmis à travers l'ensemble des parois.
F = (S1 U1+S2 U2 + S3 U3+S4 U4 ) (qi -qe).
Calculer F.
F = 236,46*30 =7093,8 ~7,1 103 W. (7,1 kW)
Le prix moyen du kWh d'électricité est 0,076 €.
Calculer
le coût C du fonctionnement d'un chauffage qui permettrait de compenser
les perrtes thermiques par transmission au travers les parois pendant
10 jours de froid.
10 jours = 24*10 = 240 heures.
Energie consommée : 7,0938 *240 =1,7 103 kWh
C = 1,7 103 *0,076 = 129 €.
|
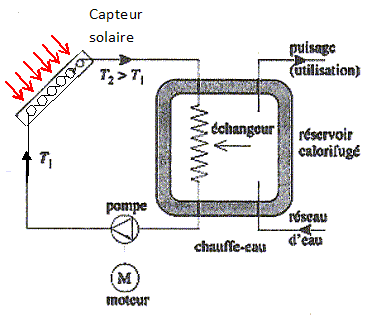
Chauffe solaire.
Un chauffe solaire
comprend un capteur solaire constitué par des tubes de cuivre dans
lesquels unu fluide dit "caloporteur" ( dans ce cas de l'eau ) est mis
en circulation par une pompe entraînée par un moteur électrique (
circuit primaire ). Ce fluide passe dans un échangeur immergé dans
l'eau contenue dans un réservoir calorifugé.
Le débit assuré par la pompe est Dv =18 L h-1. Le diamètre des tubes de cuivre est D = 5,0 mm.
La surface du capteur est S = 3,0 m2. La puissance solaire, par unité de surface, disponible pendant la période d'essai est en moyenne P= 800 W m-2.
Le moteur électrique a une puissance Pm =60 W. reau = r = 1,0 103 kg m-3. Capacité thermique massique de l'eau C = 4180 J kg-1 K-1.
Calculer la vitesse v de circulation de l'eau dans le circuit primaire.
v = Dv / (0,25 p D2) avec Dv = 18 10-3 / 3600 =5,0 10-6 m3 s-1.
v = 5,0 10-6 /(0,25*3,14 (5,0 10-3)2) =0,25465 ~0,25 m/s.
Calculer le débit massique de l'eau, noté Dm.
Dm =Dv * r =5,0 10-6 *1,0 103 = 5,0 10-3 kg s-1.
Lors d'un essai, l'eau du circuit primaire rentre à la température q1 =15°C et sort à la température q2 =50°C. La puissance thermique utile du circuit primaire est de la forme :
Putile = Dm C Dq.
Justifier cette expression et faire l'application numérique.
Energie gagnée par l'eau chauffée par le soleil : Q = masse d'eau * C (q2-q1)
Putile =Energie gagnée par l'eau chauffée par le soleil / durée (s)
Putile =masse d'eau / durée* C (q2-q1) = Dm C Dq.
Putile =5,0 10-3 *4180*(50-15) =731,5 ~7,3 102 W.
Calculer le rendement du circuit primaire.
Ce rendement est égal au rapport de la puissance thermique utile par la somme des puissances que le circuit primaire reçoit.
h =Putile / (P S+Pm) =731,5 / (800*3 +60) =0,297 ~0,30 ( 30 %).
Un bilan de fonctionnement établi sur 3 jours a donné les résultats
suivants : on a récupéré 350 L d'eau chaude à 45°C du réservoir
calorifugé. Cette eau était initialement à la température de 12°C. Le
circuit primaire a fonctionné 8 heurs par jour.
Calculer l'énergie fournie par l'installation en 3 jours.
Energie gagnée par l'eau chauffée par le soleil : Q = masse d'eau * C (q2-q1) = 350*4180*(45-12) =4,8279 107 ~4,8 107 J.
En déduire le rendement énergétique de l'installation.
Energie reçue du soleil : 800*3*8*3600 =6,912 107 J.
Energie fournie par le moteur : 60*8*3600 =1,728 106 J.
6,912 107 +1,728 106 =7,085 107 J.
Rendement = 4,8279 107 / 7,085 107 = 0,68 ( 68 %).
Solution aqueuse.
Pour éliminer le carbonate de calcium CaCO3 restant sur le revêtement dallé d'une terrasse, on fait agir de l'acide chlorhydrique ( H3O+ + Cl- ).
Ecrire l'équation de la réaction entre les ions oxonium H3O+ et le carbonate de calcium, sachant qu'il se forme des ions calcium Ca2+, du dioxyde de carbone CO2 et de l'eau H2O.
CaCO3 (s) +2H3O+ aq = Ca2+aq + CO2(g) + 3H2O(l). (1)
On utilise V0 =10
L d'une solution commerciale concentrée d'acide chlorhydrique obtenue
par dissolution de 10 moles de chlorure d'hydrogène par litre d'eau. On
considère que le volume de la solution obtenue n'a pas changé après
dissolution du chlorure d'hydrogène. On dilue alors, en ajoutant de
l'eau, pour obtenir 50 L de solution.
Calculer la concentration molaire de la solution ainsi obtenue.
Concentration de la solution mère : C0 = 10 mol dans 1,0 Ld'eau soit 10 mol /L.
Facteur de dilution F = 50 / 10 = 5,0.
Concentration de la solution diluée : C = C0/5 =10/5 = 2,0 mol/L.
Quel est le nombre de moles d'ions H3O+ présents ?
n = C0 V0 =10*10 = 100 mol.
On verse la totalité de la solution diluée sur la terrasse. 10% seulement d'ion H3O+ contenus dans la solution réagissent sur le dépôt de carbonate de calcium.
Calculer
la masse de carbonate de calcium éliminé.
On donne M(C) =12 g/mol ; M(O) = 16 g/mol ; M(Ca) = 40 g/mol.
M(CaCO3) = 40+12+3*16 =100 g/mol ; n(H3O+) = 10 mol.
D'après les nombres stoechiomètriques de l'équation (1) : n(CaCO3) = ½n(H3O+) = 5,0 mol.
Masse de solide éliminée : n(CaCO3)
M(CaCO3) =5,0 *100 = 500 g = 0,50 kg.
|
|
