|
Un jeu d'enfant : ressort vertical : bac S Liban 2011. |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
|
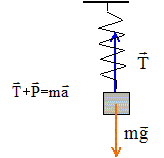
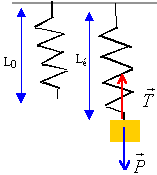
Le jouet ci-contre est constitué d’une figurine décorative accrochée à un ressort à fixer au plafond d’une chambre d’enfant. Les élèves font des expériences avec ce jouet afin de réinvestir leurs connaissances sur les mouvements oscillants et de déterminer les caractéristiques du système étudié. Dans toute l’étude, on négligera les forces de frottements et la poussée d’Archimède.  Mesures de période. La figurine est éloignée verticalement vers le bas de sa position d’équilibre puis abandonnée. Décrire le mouvement de la figurine. La figurine décrit un mouvement de va et vient autour de la position d'équilibre : mouvement sinusoïdal périodique libre ( frottements négligés ). Définir la période du mouvement. La période est la durée au bout de laquelle le mouvement redevient identique à lui même ( passage par la même position et dans le même sens ). Les élèves veulent déterminer la période du mouvement. À l’aide d’un chronomètre, ils obtiennent une durée égale à 13,8 s pour 10 périodes. Pourquoi ont-ils mesuré plusieurs périodes ? L'erreur sur la mesure est à peu près la même que l'on mesure une période ou 10 périodes. En mesurant 10 périodes, on augmente la précision. Quelle est la valeur d’une période ? T = 13,8 / 10 = 1,38 s. Afin de déterminer la constante de raideur du ressort, ils décrochent la figurine, suspendent à sa place différentes masses marquées, de valeur m. Lorsque la masse marquée est à l’équilibre, ils mesurent la longueur Lé du ressort. La longueur du ressort à vide est L0 = 25,5 cm. On prendra g = 9,8 N.kg-1. Faire un bilan des forces qui s’exercent sur la masse marquée et le représentersur un schéma. En étudiant l’équilibre de la masse marquée, établir l’expression de k, constante de raideur du ressort en fonction de m, g, L0 et Lé.
Les élèves étudient maintenant l’influence de la masse sur la période T du mouvement.
Quelle est l’influence de la masse sur la période T ?
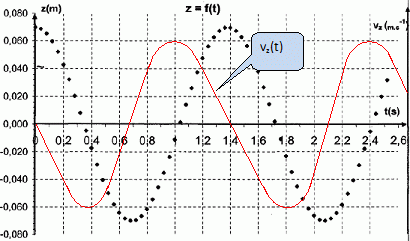
La figurine en mouvement vertical est ensuite filmée à l’aide d’une webcam. On déclenche l’enregistrement lorsque la figurine passe par sa position la plus haute. À l’aide d’un logiciel de traitement vidéo, on obtient la courbe (figure 1) et le tableau (figure 2) donnés. La coordonnée z représente la position du centre d’inertie G de la figurine sur un axe vertical, orienté vers le haut et ayant pour origine la position à l’équilibre. Déterminer la période et l’amplitude du mouvement. 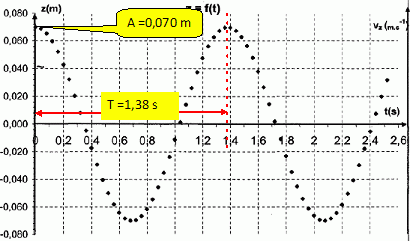 En utilisant les données expérimentales du tableau figure 2, déterminer par un calcul simple une valeur approchée de la coordonnée vz de la vitesse du centre d’inertie G à l’instant t = 0,24 s. 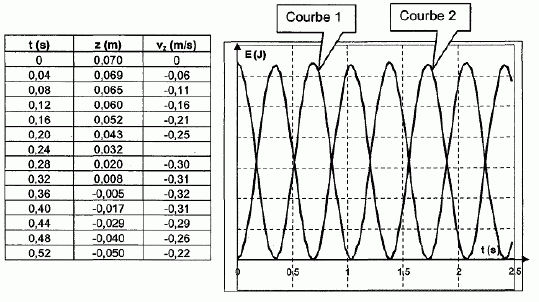 z(t = 0,20 ) =0,043 m ; z(t = 0,28 ) =0,020 m ; vz(t=0,24 ) = [z(t = 0,28 )-z(t = 0,20 )] / (0,28-0,20) = -0,023 / 0,08 = -0,2875 ~-0,29 m/s.
Le logiciel utilisé permet de calculer à chaque instant, l’énergie cinétique et l’énergie potentielle totale de la figurine. On obtient alors les courbes de la figure 3. Laquelle des deux courbes proposées correspond à l’énergie cinétique ? Justifier. 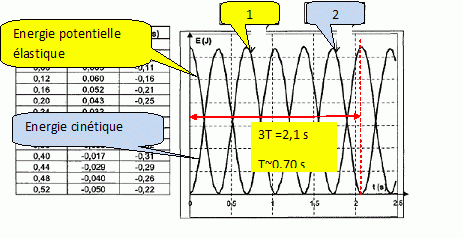 Initialement la vitesse est nulle : l'énergie cinétique initiale est donc nulle ( courbe 2). Initialement z(t) est égale à l'amplitude : l'énergie potentielle élastique est maximale ( courbe 1). Comparer la période des énergies à la période de l’oscillateur. La période des énergies est égale à la moitié de la période des oscillations. En quoi ces dernières courbes montrent-elles que les forces de frottement peuvent être négligées ? L'énergie mécanique est égale à la somme de l'énergie potentielle et de l'énergie cinétique. Le graphe indique que l'énergie mécanique est constante. Les frottements sont donc négligeables. |
|||||||||||||||||||||||
|
|