Moteur à courant continu  : bac STi génie électrotechnique  2010 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. . . .

Etude d'un moteur à courant continu. La plaque signalétique du moteur à excitation série donne les valeurs suivantes : UN =760 V ; IN =680 A ; RT =46,2 mW ; nN =1125 tr/min ; PN =480 kV. Modèle équivalent du moteur en régime permanent : 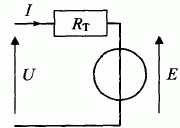RT = Ri + Re représente la résistance totale des circuits induit ( Ri) et inducteur ( Re) de la machine. E est la force électromotrice de la machine. On donne la caractéristique à vide E = f(Ie) de la machine pour une fréquence de rotation n maintenue constante à 1125 tr/min. Ie est l'intensité du courant circulant dans le circuit d'excitation ( l'inducteur). La courbe E = f(Ie) n'est linéaire que pour une intensité Ie inférieure à 700 A. .   Comment s'appelle le phénomène qui apparaît pour une intensité Ie supérieure à 700 A ? Saturation du circuit magnétique de l'inducteur. Dans toute la suite, on suppose que l'on se trouve toujours dans la partie linéaire de la courbe. Dans le cas particulier du moteur à excitation série, l'induit et l'inducteur sont traversés par  un courant de même intensité Ie = I ( I intensité du courant dans l'induit ). A partir du modèle équivalent du moteur à courant continu à excitation série, donné une relation liant U, E, RT et I. U = E + RT I. Le flux à travers la machine est proportionnel à l'intensité du courant dans l'inducteur.. Montrer que l'on peut écrire pour ce moteur E = k I W, avec k une constante, I l'intensité du courant parcourant le moteur et W la vitesse de rotation de son arbre ( en rad/s) . Le flux F est proportionel à l'intensité du courant inducteur : F = k1 Ie = k1I. La force électromotrice E est proportionnelle au flux F et à la vitesse de rotation W : E = k2 F W = k2 k1IW = k IW. A l'aide de la courbe E = f(Ie) montrer que k = 9,1 10-3 V s A-1 rad-1. 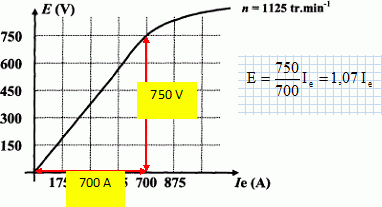1,07 V A-1 =k W avec W = 2 p n / 60 = 2*3,14*1125 / 60 =117,75 rad/s. k = 1,07 /  W =1,07 / 117,75 = 9,1 10-3 V s A-1 rad-1. Montrer que le moment du couple électromagnétique peut s'écrire Tem = kI2. Expression de la puissance électromagnétique :  Tem W = E I avec E = kWI d'où : TemW =kWI2. Par suite Tem = kI2. Etude au régime nominal. Déterminer : la force électromotrice EN. EN =UN -RT IN = 760-0,0462* 680 = 729 V. le moment TemN du couple électromagnétique. TemN = k I2N  =9,1 10-3 *6802= 4207 Nm. le moment TuN du couple utile. TuN = PN / WN avec  WN= 2p n/60 = 6,28*1125 / 60 = 117,75 rad/d. TuN =  480000 / 117,75 = 4076 Nm. le moment TP du couple de pertes. TP = TemN - TuN =4207-4076 =131 Nm. la puissance absorbée PaN. PaN= IN UN =680 *760=516,8 kW. le rendement hN. hN =PN /PaN = 480 / 516,8 =0,93. Etude à régime variable. On peut être amené à faire tourner la machine à vitesse réduite. On supposera que la valeur du couple électromagnétique reste égale à sa valeur nominale. Montrer que dans ces conditions I= IN. Tem = kI2 ; TemN = kIN2 ; Tem =TemN conduit à I = IN. Montrer que la tension U a pour expression U = 0,647 n +31,4 avec  la fréquence n de rotation en tour/min. U= E+RT I ; E = k W I= k 2 p n/60 I ; U = k 2 p n/60 I +RT I U= 9,1 10-3 *6,28 / 60 *680 n + 0,0462 *680 ; U = 0,647 n + 31,4. Calculer  U si n = 600 tr/min. U = 0,647 *600 +31,4 = 419,6 ~420 V.

menu