Mathématiques. DNB Polynésie 09 /2025. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . ... . . . . .. .. ...... ... Exercice 1. 22 points On veut poser du carrelage sur le sol intérieur d'une maison. Le carreleur A fait payer 80 € par m². Le carreleur B fait payer 60 € par m² auxquels il faut ajouter 970 € pour la mise en place du chantier. 1. Montrer que pour une surface dont l’aire est de 20 m², le prix est de 1 600 € avec le carreleur A et de 2 170 € avec le carreleur B. A : 20 x80 = 1600 €. B : 20 x60 +970 = 2 170 €. 2. Calculer le prix à payer pour une surface dont l’aire est 60 m² avec le carreleur A, puis avec le carreleur B. A : 60 x80 = 4800 €. B : 60 x60 +970 = 4 570 €.  3. On désigne par x l’aire de la surface à carreler exprimée en m².  On appelle f la fonction qui à l’aire à carreler en m2 associe le prix en euros à payer avec le carreleur A. On admet que f est définie par f(x)= 80 x.  On appelle g la fonction qui à l’aire à carreler en m2 associe le prix en euros à payer avec le carreleur B. On admet que g est définie par g(x) = 60x + 970. a. Quelle est l'image de 70 par la fonction f ? f(70) = 80 x70 = 5 600 €. b. Quel est l'antécédent de 2 400 par la fonction f ? 2400 / 80 =30 m2.  c. Sur le graphique fourni, on a tracé la représentation graphique de la fonction g. Tracer la représentation graphique de la fonction f sur ce même graphique. 4. En utilisant le graphique fourn, estimer l'aire maximale en m² que l'on peut carreler avec un budget de 2 800 € si l'on choisit le carreleur B. 5. Calculer l’aire en m² pour laquelle on paie exactement le même prix avec le carreleur A et le carreleur B. 80 x = 60 x+970 ; 20 x = 970 ; x = 970 / 20 =48,5 m2. Exercice 2 (20 points).  Cet exercice est un questionnaire à choix multiple (QCM). Pour chaque question, quatre réponses sont proposées. Une seule réponse est exacte. Recopier sur la copie le numéro de la question et la réponse choisie. Aucune justification n'est demandée. Question 1 La formule qui permet d’obtenir la pointure de chaussure p à partir de la longueur L du pied, exprimée en centimètres, est p = 1,5(L+1). Quelle est la pointure d’un pied de longueur 25 cm ? p = 1,5 (25+1) =39. Question 2 Le triangle MUR,rectangle en U, qui est représenté n’est pas en vraie grandeur. Quelle est la mesure de l'angle RMU arrondie au degré ? 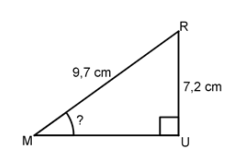sin(MUR) = RU / RM = 7,2 / 9,7 =0,742. L'angle mesure environ 48 °. Question 3 Un coureur a remporté la course du 100 m en 10 secondes exactement. À quelle vitesse moyenne en km / h a-t-il parcouru cette distance ? 100 / 10 = 10 m /s ou 10 x3,6 = 36 km /h. Question 4 Roxane a acheté le modèle réduit d’un tableau célèbre à l’échelle 1 / 20 . La largeur du modèle réduit est 7 cm. Quelle est la largeur réelle du tableau ? 7 x20 = 140 cm. Question 5 Trois points nommés A, B, et C sont positionnés sur la sphère ci-contre. Quel point a pour coordonnées (65° N ; 30°O) ? 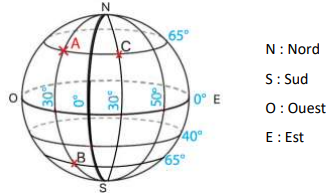Point A. Exercice 3 (16 points)  On s'intéresse au motif dessiné ci-dessous que l'on retrouve dans un pavage recouvrant un mur du palais de l'Alhambra en Espagne. Ce motif est partagé en douze losanges superposables numérotés de 1 à 12. Dans chaque losange, les côtés ont pour longueur 5 cm, les angles aigus mesurent 60° et les angles obtus mesurent 120°. Partie 1 Dans cette partie, aucune justification n'est demandée.  1. Quelle est l'image du losange ① par la symétrie centrale de centre A ? Losange 7. 2. Quelle est l'image du losange ③ par la symétrie axiale d'axe (AF) ? Losange 5.  3. Quelle est l'image du losange ⑦par la rotation de centre A qui transforme le losange ③ en le losange ⑪ ? Losange 3.  4. Quelle est l’image du losange ⑧par la translation qui transforme A en E. Losange 5. Partie 2 Louis a remarqué que le motif donné dans l’énoncé s'obtient à partir de l'hexagone ABCDE en appliquant plusieurs fois la même rotation de centre A. Il souhaite tracer le motif avec le logiciel Scratch en prenant 10 pas pour 1 cm. Le bloc dont le script est proposé permet de tracer la figure représentée ci-dessous sur laquelle la flèche indique l’orientation du lutin au début du programme : 1. Compléter les lignes 3, 4 et 5 afin que le bloc « hexagone ABCDEF » trace l'hexagone ABCDEF de côté 5 cm en partant du point A. Aucune justification n’est attendue. 2. Parmi les trois scripts proposés ci-dessous, lequel permet de tracer le motif en utilisant le bloc hexagone ABCDEF précédent ? Aucune justification n’est attendue. ... =  = .... Exercice 4 (23 points)  Lorsque la neige vient à manquer en montagne, certaines stations de ski utilisent des canons à neige pour enneiger les pistes. Les parties 1 et 2 sont indépendantes.  Partie 1 On cherche à estimer le coût de l’eau nécessaire pour l'utilisation de canons à neige sur les pistes françaises pour produire une hauteur de 30 cm de neige. Pour produire 2,5 m³ de neige, il faut 1 m³ d’eau. Le prix de l’eau pour 1 m³ est 4,30 €. On rappelle que 1 hectare = 10 000 m². On donne la formule V = S x h pour calculer le volume de neige à produire en fonction de l’aire de la piste et de la hauteur de neige souhaitée.  V représente le volume de neige à produire exprimé en m3 ; S représente l’aire de la piste exprimée en m2 ; h représente la hauteur de neige exprimée en m. 1. On s’intéresse à une piste dont l’aire est 1 hectare. a. Vérifier que pour enneiger cette piste sur une hauteur de 30 cm, il faut prévoir 3 000 m³ de neige. 10 000 x0,30 = 3 000 m3.  b. En déduire qu’il faut prévoir 1 200 m³ d'eau pour enneiger cette piste sur une hauteur de 30 cm. 3 000 / 2,5 =1 200 m3. c. Montrer que le coût de 1 200 m3 d’eau est 5 160 €. 1 200 x 4,30=5 160 €. 2. a. L’ensemble des pistes de ski françaises occupent une surface de 25 000 hectares. Quel serait le coût de l’eau si on utilisait les canons à neige sur l’ensemble des pistesfrançaises ? 5 160 x 25 000=1,29 108€. b. En réalité, les canons à neige ne sont utilisés que sur 9 250 hectares de pistes. Calculer le pourcentage de la surface totale des pistes de ski sur laquelle sont utilisés des canons à neige. 9 250 / 25 000 =0,37 ( 37 %). Partie 2 Un skieur qui pratique le ski de fond dispose d’un plan représenté par la figure ci-dessous. Les droites (EB) et (KD) sont parallèles.  1. Quelle est la longueur du segment [FD] ? FD = 2 x ED = 600 m. 2. Calculer la longueur du segment [AF] arrondie au m. cos 30 = AC / AF ; AF = AC / cos 30 = 400 / 0,866 =462 m. 3. a. Montrer que la longueur du segment [EB] est égale à 500 m. Relation de Pythagore dans le triangle EDB rectangle en D : EB2 = ED2 +BD2 =3002+4002=250 000 ; EB = 500 m.  b. Calculer la longueur du segment [DK]. Relation de Thalès : EB / DK = EH / DH = 2 ; DK = EB / 2 = 250 m.  4. En déduire la longueur du parcours qui passe par les points A, F, E, D et K. AF + FD +DK = 462 +2 x300 +250 = 1 312 m. Exercice 5 (19 points)  Une étude montre qu’un nombre important de nos vêtements reste dans les placards et n’est pas utilisé. Six amis décident de donner chacun une partie de leurs vêtements à une association lors d’une journée de collecte organisée dans leur village. 1. Inès compte 20 tee-shirts dans son placard et souhaite en donner 70% à l’association. Montrer qu’elle va en donner 14. 20 x0,70=14.  2. La feuille de calcul ci-dessous indique le nombre de tee-shirts que chacun des amis souhaite donner à cette association. 1 A B C D E F G H 2 Inès Sylvain Sabrina Marco Yuna Axel Total 3 Nombre de tee-shirts à donner 14 6 9 11 12 8 a. Quelle formule peut-on saisir dans la cellule H2 pour obtenir le nombre total de tee-shirts à donner ? somme(B3 : G3)  b. Les amis réunissent tous les tee-shirts qu’ils vont donner. Calculer la probabilité qu’un tee-shirt pris au hasard appartienne à Yuna. 12 / (14+6+9+11+12+8)=12 / 60 = 0,2. c. Calculer le nombre moyen de tee-shirts donnés par chacun des amis. 60 / 6 = 10.  d. Quelle est la médiane du nombre de tee-shirts donnés ? 6 ; 8 ; 9 ; 11 ; 12 ; 14. La médiane est comprise entre 9 et 11. 3. A la fin de la journée de collecte des vêtements, l’association a récolté un total de 168 tee-shirts et 63 pantalons. Cette association souhaite réaliser des lots identiques contenant chacun le même nombre de pantalons et le même nombre de tee-shirts en utilisant tous les vêtements donnés. a. Peut-elle réaliser 4 lots ? Peut-elle réaliser 3 lots ? 63 n'est pas un multiple de 4 : on ne peut pas réaliser 4 lots. 63 et 168 sont des multiples de 3 : on peut réaliser 3 lots.  b. Déterminer la décomposition en produit de facteurs premiers de 168 et de 63. 168 = 23 x3 x7. 63 = 32 x7. c. Quel nombre maximum de lots pourra-t-elle réaliser ? PGDC(168 ; 63) = 21. On peut réaliser au maximum 21 lots.

menu