Mathématiques, physique chimie. Bac STL Nlle Calédonie 2025.

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

.
. . . .

.
.
.. ..
......


...
  Exercice 1 (5 points) : Datation au carbone 14
Le carbone possède deux isotopes stables : le carbone 12 (très majoritaire dans la nature) et le carbone 13 (minoritaire). Le carbone 14 est un isotope radioactif du carbone. Les scientifiques s’en servent pour estimer l’âge d’objets anciens : œuvres d’art, fossiles… Cet exercice a pour objectif d’étudier la désintégration radioactive du carbone 14.
 1. Donner la composition des noyaux de carbone 126C et 146C
126C : 6 protons et 6 neutrons ; 146C 6 protons et14-6 = 8 neutrons.
 2. Indiquer pourquoi ces noyaux sont qualifiés d’isotopes.
Ils ont le même nombre de protons et des nombres de neutrons différents.
Le carbone 14 subit une désintégration de type ß- .
3.  Recopier sur sa copie et compléter l’équation de la réaction nucléaire suivante :
146C -->147N+ 0-1e .
 La loi de désintégration radioactive suit l’équation : dN(t) = –l N(t) /dt ; où N(t) est le nombre de noyaux radioactifs à l’instant t, et l est la constante de la désintégration, avec l > 0. Ainsi le nombre de noyaux radioactifs vérifie l’équation différentielle du 1er ordre : (E) : y ’ = – l y où y est une fonction de la variable réelle t, exprimée en année, définie et dérivable sur [0 ; +∞[. La fonction y représente le nombre de noyaux radioactifs.
4. En considérant y(0) = 100, montrer que pour t ≥ 0 : y(t) = 100 exp( – λt ).
Solution générale de l'équation y(t) = A exp(-lt) avec A une constante réelle.
y(0) = 100 = A.
y(t) = 100 exp(-l t).
5. Déterminer la limite de y(t) lorsque t tend vers +∞.
Le terme en exponentielle tend vers zéro et y(t) tend vers zéro.
6. Résoudre l’équation y(t) = 50. Donner la réponse en fonction de l.
50 =100 exp(-lt) ; 0,5 = exp(-lt)  ; ln(0,5) = -ln(2)= -l t ; t = ln(2) / l.

7. Déterminer graphiquement la valeur du temps de demi-vie t½. La construction graphique doit apparaître .

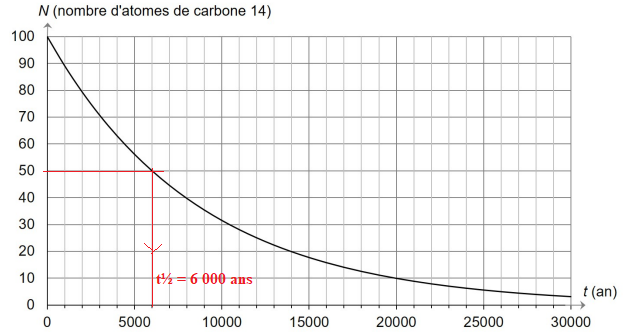
. On sait que : t½ = ln(2) / l .
8.  En déduire la valeur de la constante de désintégration l. En donner une valeur arrondie à 10– 5 .
l = ln(2) / 6000~1,2 10-4 an-1.

Exercice 2. 6 points. Comprimé effervescent d'aspirine.
On étudie ici l’intérêt d’utiliser un comprimé effervescent d’aspirine plutôt qu’un comprimé ordinaire.
Données
Formule brute de l’acide acétylsalicylique : C9H8O4 .
 Masse molaire moléculaire de l’acide acétylsalicylique : M = 180 g·mol–1 .
 L’ion acétylsalicylate de formule brute C9H7O4 – est la base conjuguée de l’acide acétylsalicylique.
Couple acide-base C9H8O4 (aq)/ C9H7O4 – (aq) : pKa = 3,5 à 25 °C.
L’acide acétylsalicylique est peu soluble dans l’eau (3 g L –1 à 20 °C). Le salicylate de sodium NaC9H7O4 est très soluble dans l’eau.
L’acide acétylsalicylique est lipophile, il pénètre la paroi de l’estomac et cause des irritations. La formule semi-développée de l’acide acétylsalicylique est donnée ci-après.

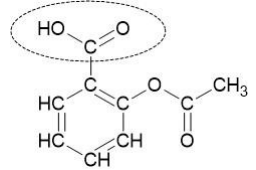
1. Nommer la fonction chimique associée au groupe caractéristique entouré sur la représentation précédente.
Fonction acide carboxylique.
Ce groupe caractéristique de la molécule est à l’origine des propriétés acides de l’acide acétylsalicylique. Sa base conjuguée est l’ion acétylsalicylate C9H7O4 – .
2. Représenter sur votre copie la formule semi-développée de l’ion acétylsalicylate.

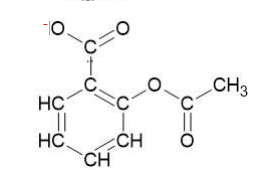3. En comparant la formule semi-développée de l’acide acétylsalicylique et celle de l’ion acétylsalicylate, proposer une interprétation de la différence de solubilité dans l’eau entre les deux espèces chimiques correspondantes.
L’ion acétylsalicylate est plus polaire que l’acide acétylsalicylique ; l'eau est un solvant polaire. L’ion acétylsalicylate est plus soluble dans l'eau que l'acide acétylsalicylique.

Dissolution d’un comprimé ordinaire d’aspirine.
 Un comprimé ordinaire d’aspirine contient 500 mg d’acide acétylsalicylique. Il est broyé et placé sous agitation dans un volume V = 200 mL d’eau distillée. La dissolution de l’aspirine est lente et complète. On mesure le pH de la solution obtenue : pH = 2,7.
4. Déterminer la valeur de la concentration en quantité de matière apportée en acide acétylsalicylique dans la solution obtenue, notée C0 (en mol·L–1).
n =masse (g) / masse molaire ( g / mol) = 0,500 / 180 =2,78 10-3 mol.
C0 = n / V = 2,78 10-3 / 0,200 =1,39 10-2 mol / L.
L’acide acétylsalicylique est un acide faible dans l’eau. L’équation de la réaction chimique associée est :
 C9H8O4 (aq) + H2O(l) = C9H7O4 – (aq) + H3O + (aq).
5.  Donner la définition d’un acide (selon Brönsted) ainsi que celle d’un acide faible.
Un acide est une espèce, ion ou molécule, susceptible de libérer un proton H+.
Un acide faible réagit partiellement avec l'eau.
L’expression du coefficient de dissociation a de l’acide acétylsalicylique dans l’eau s’écrit : a = [H3O + ] /C0 . Montrer que le coefficient de dissociation a pour valeur  0,14. Expliquer pourquoi cette valeur confirme que l’acide acétylsalicylique est un acide faible.
a=10-2,7 / (1,39 10-2)=0,14.
a est très inférieur à 1 : cet acide est qualifié de faible.

Dissolution d’un comprimé effervescent d’aspirine
On utilise maintenant un comprimé effervescent d’aspirine. Le comprimé effervescent contient 500 mg d’acide acétylsalicylique, ainsi que de l’hydrogénocarbonate de sodium NaHCO3 (s). On place le comprimé dans un volume V = 200 mL d’eau distillée. On observe un dégagement gazeux important. La dissolution du comprimé est rapide et complète. Le pH de la solution obtenue a pour valeur : pH = 5,8.
 Données : - Le diagramme de prédominance dans l’eau (à 25°C) pour les couples associés à l’ion hydrogénocarbonate, est donné ci-après sans souci d’échelle :

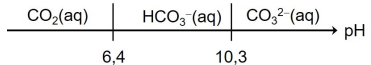
Le dioxyde de carbone gazeux CO2(g) est peu soluble dans l’eau.
7. En utilisant le diagramme de prédominance précédent, proposer une interprétation au dégagement gazeux observé.
A pH=5,8, la forme CO2 prédomine. Ce dernier est peu soluble dans l'eau. Il se dégage.
 8. Représenter le diagramme de prédominance pour le couple associé à l’acide acétylsalicylique. En déduire l’espèce prédominante dans la solution obtenue.

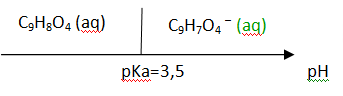
A pH = 5,8 la forme C9H7O4 – .  prédomine.
9.  Proposer une explication à la meilleure solubilité de l’aspirine dans l’eau avec un comprimé effervescent.
La forme C9H7O4 – .  polaire prédomine. L'eau est un solvant polaire.
10. Déduire des questions précédentes et des données, pourquoi l’utilisation d’un comprimé effervescent d’aspirine irrite moins la paroi de l’estomac que l’utilisation d’un comprimé ordinaire d’aspirine.
Le pH de la solution d'aspirine effervescente est peu acide ( pas de brûlure d'estomac).

... =  =
....
EXERCICE 3 (4 points)
(Mathématiques)
Partie A.
On donne ci-dessous la courbe représentative d'une fonction f définie sur R.

La représentation graphique de la fonction dérivée f ' de la fonction f peut être :
Sur ]-oo ; -1 ] et sur [2 ; +oo[ ] f(x) est croissante : f '(x) est positive.
Sur [-1 ; 2] f(x) est décroissante : f '(x) est négative.

Partie B.
 Une cuve est remplie d'un mélange gazeux contenant initialement 80 % de diazote. En raison d'une fuite, cette cuve perd chaque seconde 0,3 L du mélange gazeux. Pour compenser cette perte, on injecte 0,3 L de diazote par seconde afin que la cuve reste en permanence pleine. On note f(t) la proportion du volume de diazote dans cette cuve à l'instant t exprimé en seconde, avec t dans [0 ; + ∞[. On admet que la fonction f est de la forme f(t) = k exp(-0,02t) + 1.
1.a. D’après l’énoncé, donner la valeur de f (0).
f(0)=0,80=k+1 ; k = -0,2.
b. En déduire que f (t) = – 0,2exp(-0,02t) + 1 pour t dans [0 ; + ∞[.
f(t)= -0,2exp(-0,02t) +1.
2. On note f ' la fonction dérivée de la fonction f. Calculer f '(t) et en déduire les variations de la fonction f sur [0 ; + ∞[.
f '(t) = -0,2 x(-0,02) exp(-0,02t) =0,004 exp(-0,02t).
f '(t) strictement positive  ; f(t) est strictement croissante.
 3. Calculer la limite de la fonction f en +∞ et interpréter ce résultat dans le contexte de l'exercice.
exp(-0,02t)  tend vers zéro si t tend vers +oo.
f(t) tend vers 1.
Au bout d'un temps suffisamment long, la cuve est pleine de diazote.
 4.a. Déterminer le temps, exprimé en seconde, à partir duquel la proportion du volume de diazote dans la cuve sera supérieure ou égale à 95 %.
-0,2exp(-0,02t) +1 >0,95 ;
 1-0,95 > 0,2exp(-0,02t)
0,05 /0,2 >exp(-0,02t)
 0,25 >exp(-0,02t).
ln(0,25)= -ln(4) > -0,02 t ;
t > ln(4) / 0,02) ; t >69  s.

4.b. On considère le programme Python suivant :
from math import exp
def temps() :
t = 0
while – 0,2 * exp(– 0,02 * t)+1 <= 0,95
t =t+1
 return t
Compléter les pointillés pour que l'exécution de temps() renvoie le nombre entier correspondant au temps en seconde à partir duquel la proportion de diazote dans la cuve est supérieure ou égale à 95 %.


EXERCICE 4 : Toujours plus haut ! (5 points)
(physique-chimie)
The fall guy ! Ou l’homme qui tombe à pic !
Dans les films les risques pris par les cascadeurs restent tout de même « calculés ». Nous étudions dans cet exercice une scène de chute d’un cascadeur depuis le haut d’un immeuble. Pour cette étude, on choisit le référentiel terrestre, supposé galiléen, auquel on adjoint un repère d’espace (Oy) vertical orienté vers le haut . L’origine O du repère est prise au niveau du sol, au bas de l’immeuble. Le cascadeur tombe du haut de l’immeuble sans vitesse initiale au point A, d’abscisse yA = h à la date t = 0.
Données  Masse du cascadeur : m = 80 kg.
 Hauteur de chute : h = 15 m.
 Intensité du champ de pesanteur, supposé uniforme : g = 9,81 m·s–2 .
 On suppose que l’action de l’air sur le cascadeur pendant sa chute est négligeable devant les autres actions mécaniques.
1. Effectuer un bilan des forces extérieures appliquées au système {cascadeur} pendant la chute.
Le cascadeur n'est soumis qu'à son poids, verticale vers le bas, valeur P = mg.
2. En appliquant la deuxième loi de Newton, établir la relation entre le vecteur accélération a du système {cascadeur} et le champ de pesanteur g.
Sur l'axe vertical orienté vers le haut, la seconde loi de Newton conduit à : a = -g.

3. Après avoir donné la coordonnée suivant l’axe (Oy) du vecteur accélération, établir que la loi horaire vérifiée par la coordonnée vy du vecteur vitesse  est : vy(t) = – g × t.
La vitesse est une primitivse de l'accélération : v(t) = -gt + constante.
La vitesse initiale étant nulle v(t) = -gt.
4. En déduire la loi horaire du mouvement du cascadeur y(t).
La position est une primitive de la vitesse : y(t) = -½gt2 + constante.
y(0) = h ; y(t) =-½gt2 +h.
5. Sachant que la chute dure 1,75 s, calculer la coordonnée vy du vecteur vitesse au bas de l’immeuble.
vy = -9,81 x1,75 ~ -17,2 m/s.

6. Vérifier que la norme du vecteur vitesse  avec laquelle le cascadeur arrive au bas de l’immeuble a pour valeur v = 17,2 m·s–1 . On installe au bas de l’immeuble un dispositif pour amortir l’arrivée du cascadeur. Le dispositif peut se déformer sans risque de blessure pour un homme jusqu’à 15 kJ d’énergie cinétique. Déterminer s’il y a un risque de blessures pour le cascadeur.
½mv2 =0,5 x80 x17,22 = 1,18 104 J = 11,8 kJ < 15 kJ.
Il n'y a pas de risque pour le cascadeur.





  
menu