résumé
de cours
fiche
bac
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
..
..
| .
. |
Un condensateur est constitué de deux conducteurs métalliques (les armatures) en influence mutuelle, séparés par un isolant (le diélectrique).
Un condensateur soumis à une tension u prend une charge q proportionnelle à u telle que :
u: tension électrique règnant aux bornes du condensateur en volt (V)
C: capacité du condensateur en farad (F)
le farad est une unité
représentant une très grande capacité,
rarement rencontrée en électronique ou au
laboratoire. On utilise couramment les sous multiples:
1mF=10-3F, 1µF=10-6F,
1nF=10-9F (nanofarad) et 1pF=10-12F
(picofarad)
L'énergie emmagasinée dans un condensateur de
capacité C aux bornes duquel règne une tension
u est : E = 1/2
Cu2
E: énergie électrique en joule (J)
C: capacité du condensateur en farad (F)
u: tension entre les armature du
condensateur en volt (V)
Relié à un générateur de
tension continue , le condensateur se charge : il stocke
de l'énergie.
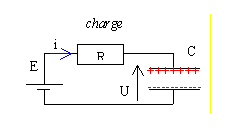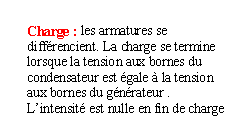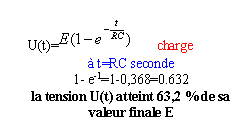
Lors de la charge du condensateur, la tension aux bornes du condensateur croît plus ou moins rapidement pour atteindre la valeur de la tension imposée par le générateur de tension constante E.
Les paramètres qui ont une influence sur la rapidité de cette évolution sont: la résistance R du dipôle ohmique et la capacité C du condensateur. E n'a aucune influence sur cette rapidité d'évolution.
Plus R est grande, plus U met de temps pour tendre vers E.
Plus C est grande, plus U met de temps pour tendre vers E.
La durée t=RC apparaît comme une durée caractéristique de l'évolution du système. t donne un ordre de grandeur du temps que met la tension U pour atteindre (à 99% près) la valeur E. On dit alors que le condensateur est chargé.
t peut être déterminé graphiquement par trois méthodes différentes:
- Méthode de la tangente à l'origine : la tangente à l'origine coupe l'asymptote à la courbe U à t = t
- Méthode des 63% : à t= t la tension U est égale à 0,67 fois sa valeur maxi soit 2*0,67 voisin de 1,3 V( exemple ci dessous)
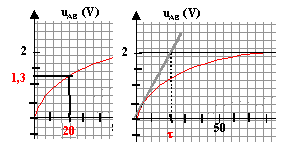
- Méthode consistant
à remarquer que le condensateur est
considéré comme chargé au bout d'une
durée t=5 t
Cette énergie stockée peut être
libérée lors de la décharge, par
exemple à travers un résistor.
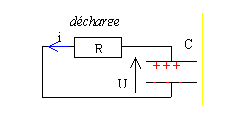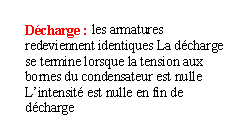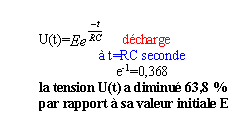
Lors de la décharge du condensateur, la tension U décroît plus ou moins rapidement de E à 0. On peut faire les mêmes observations qu'en ce qui concerne la charge.
La tensionU est une fonction continue du temps pour un cycle charge-décharge.
La tension aux bornes du dipôle ohmique est une fonction discontinue du temps pour un cycle charge-décharge. Il en est donc de même pour i.
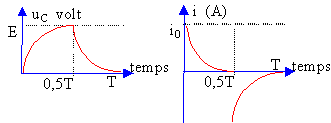
. Equations différentielles vérifiées par la tension U=uC.
Considérons d'abord la phase de charge du condensateur.
La loi d'additivité des tensions appliquée aux bornes du dipôle RC permet d'écrire: uR+uC=E
La loi d'Ohm appliquée au dipôle ohmique permet d'écrire: uR=R i.
or i = dq/ dt = q' ( dérivée de la charge par rapport au temps)
mais q=CuC => q' =CduC/dt et uR=RCduC/dt.
Finalement l'équation différentielle cherchée s'écrit: RCduC/dt+uC=E.
Le facteur t=RC apparaît bien dans l' équation différentielle.
t homogène à une durée, est appelé constante de temps du dipôle RC et s'exprime en seconde (si R est en ohm (W) et C en farad (F)). C'est une durée caractéristique du dipôle RC qui nous donne un ordre de grandeur de la durée de la charge ou de la décharge du condensateur.
Une bobine inductive est caractérisée par son inductance, notée L, grandeur positive, exprimée en heny (H). Cette bobine possède une résistance électrique, notée r (ohm).
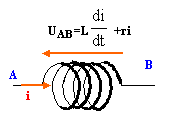
Lors de la fermeture de l'interrupteur d'un circuit possédant une bobine inductive, la bobine stocke de l'énergie ( ½Li², avec i : intensité en ampère) et en conséquence entraîne un retard à l'établissement du courant.
A l'ouverture de ce même interrupteur, la bobine restitue l'énergie stockée auparavant : cela entraîne une étincelle aux bornes de l'interrupteur.
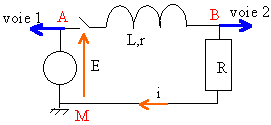
constante de temps : t = L / S résistances.
la durée du régime transitoire est voisin de 5 fois la constante de tempts t = L / (R+r) pendant cette durée la bobine stocke de l'énergie.
t à la dimension d'un temps :
Ldi/dt à la dimension d'une tension donc L à la dimension : [V] [T] [A]-1.
R est en ohm , une tension divisée par une intensité : [V] [A]-1.
L/R a la dimension : [V] [T] [A]-1 [A] [V]-1=[T]
Dans le cas d'une résistance R, la tension aux bornes et l'intensité sont proportionnelles : visualiser la tension, c'est obtenir l'image de l'intensité au facteur R près.
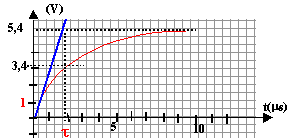
tracer la tangente à la courbe à la date t=0 : cette tangente coupe l'asymptote horizontale à la date t = t.
à la date t = t la tension aux bornes du résistor est ègale à 63% de sa valeur finale soit 5,4*0,63 = 3,4 V.
Tracer une droite horizontale passant par U = 3,4 V, l'intersection avec la courbe donne par lecture sur l'axe des temps la valeur de la constante de temps.
tensions :
tension aux bornes de la bobine : uAB= Ldi/dt + ri
tension aux bornes du résistor : uBM = Ri
r et R en ohms; L en henry ; intensité en ampère et tension en volt.
di/dt + (r+R)/ L i = E / L. équation différentielle à la fermeture de l'interrupteur.
di/dt + (r+R)/ L i = 0. équation différentielle à l'ouverture de l'interrupteur.
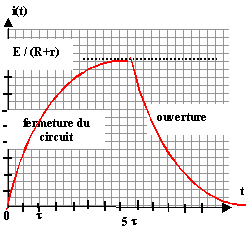
intensité :
en régime permanent ( intensité constante) di/dt =0
d'où E = R I + rI soit Imax = E / (R+r).
L'intensité est une fonction continue du temps.
Un condensateur de capacité C(farad F) initialement chargé ( charge initiale Q0 coulomb) et associé en série avec une bobine d'inductance L (henry H) , de résistance r (ohms) et un résistor dont la résistance R peut varier.On étudie la décharge du condensateur chargé à travers la bobine.
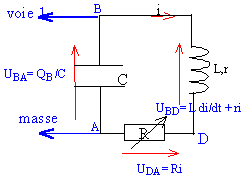
uAB = Ldi/dt + ri+Ri
avec i = -dQA/dt = -CduAB /dt et di/dt = -d²QA/dt² = -Cd²uAB /dt²
uAB = -LCd²uAB /dt² - (R+r)CduAB /dt
LCd²uAB /dt² + (R+r)CduAB /dt +uAB =0
LCu" + (R+r)C u' + u = 0. équation différentielle du circuit.
si les résistances sont négligeables :
LCu" + u = 0 soit u" + 1/(LC) u = 0
on pose w0² = 1/ (LC) ; w0 : pulsation en rad /s.
les fonctions, solution de cette équation, sont de type sinusoïdale : u = U cos(w0t)
période : 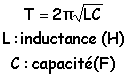
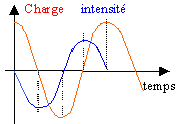
à t = 0 le condensateur est chargé, l'intensité du courant est nulle.
0<t<T0/4 : échange d'énergie entre bobine et condensateur.
le condensateur se décharge ( perte d'énergie) à travers la bobine : la bobine stocke de l'énergie
u décroit et|i| augmente : la valeur maximale de l'intensité est telle que : ½Q0²/C= ½LI²max.
à t = T0/4 : la bobine stocke l'énergie ½LI²max et le condensateur ne stocke pas d'énergie.
T0/4 <t<T0/2 : échange d'énergie entre bobine et condensateur.
le condensateur se charge ( gain d'énergie) en sens contraire de la charge précédente : la bobine déstocke de l'énergie
à t = T0/2 : la bobine ne stocke pas d'énergie et le condensateur stocke l'énergie ½Q0²/C.
si les résistances ne sont pas négligeables :
résistances pas trop grandes : oscillations pseudopériodiques
la pseudopériode rest proche de la période T0.
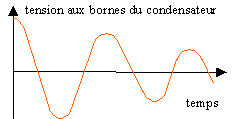
si les résistances sont grandes, on observe plus de période : régime apériodique.
Il est possible d'entretenir les oscillations en compensant à chaque instant l'énergie perdue par un apport d'énergie ( dispositif électronique simulant une résistance négative par exemple).
Dans ce cas la période des oscillations entretenues est égale à la période propre de l'oscillateur T0.