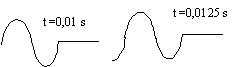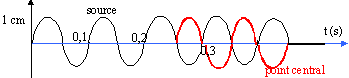
Onde le long d'un ressort :

Un piston provoque des ondes de compression et de dilatation à l'extrémité d'un ressort de longueur 1 m. La position du piston évolue de façon sinusoïdale, avec une période T=0,1s et une amplitude de 1cm. La célérité des ondes le long du ressort est de 2 m/s.

1. Au bout de combien de temps la spire située au milieu du ressort commence t-elle à osciller ? Quelle est l'amplitude des oscillations de cette spire ?
2. Représenter sur un graphe l'évolution de la position de spire située au milieu du ressort et celle du piston, pour t variant de 0 à 0,45s. Comparer l'état vibratoire de cette spire et du piston. L'onde est elle longitudinale ou transversale ?
3. Quelle est la plus petite distance séparant deux spires en phase ? Pour quelle fréquence cette distance vaut elle 5 cm ? 

Onde ultrasonore dans l'air et dans l'eau :.

Un émetteur ultrasonore est placé au point E. Le récepteur R est connecté à millivomètre particulier, qui mesure une tension proportionnelle à l'amplitude de l'onde détectée. La fréquence du générateur qui alimente l'émetteur est de 40 kHz.

1. Quelle est période T des ondes ultrasonores ? Quelle est la longueur d'onde l des ondes ultrasonores dans l'air dans ces conditions (la célérité des ultrasons est de 340 m/s) ?
2. On dispose juste derrière l'émetteur une plaque percée d'une fente de centre F, de largeur a=1 cm et de grande longueur. F et E sont sur la même horizontale. E et R sont reliés par une ficelle de longueur 0,5 m. On déplace R dans un plan horizontal passant par F. La tension relevée par le récepteur reste-t-elle constante ? Pourquoi ?
3. On appelle a l'angle que fait la perpendiculaire à l'écran et la ficelle qui caractérise la direction FR. On constate que la tension lue sur le voltmètre est nulle pour un angle a₀ = 48°. Calculer le rapport l/a et comparer cette valeur à celle de l'angle (en radian) qui correspond à une amplitude nulle.
4. On reprend cette même expérience dans l'eau : quels résultats sont modifiés ? En admettant que la conclusion de la question précédente reste valable, quelle est la valeur de l'angle correspondant à une amplitude reçue nulle ? la célérité du son dans l'eau est de 1500 m/s. 

onde progressive sinusoïdale sur une corde :

Un vibreur impose à une corde une perturbation sinusoïdale de période T. On appelle v la célérité des ondes mécaniques le long de la corde. On néglige dans tout l'exercice l'effet de la pesanteur. L'altitude (en mètres) d'un point M d'abscisse x est donnée par la relation : y_M(x,t)=0,04sin(2pt/0,01 - 2p x/0,02 )

1. Quelle est la période temporelle de l'onde qui on propage le long de la corde ? Quelle est sa longueur d'onde ?
2. Quelle est la célérité de l'onde qui se propage le long de la corde ? L'onde est elle transversale ou longitudinale ?
3. Quelle est l'amplitude des vibrations de la corde ?
4. A quelle distance de la source se situe le point M ? Si une perturbation est émise à l'instant t=0 au niveau de la source, à quel instant t cette perturbation atteint-elle le point M ? Comment appelle-t-on cette durée ?
5. Si S est l'extrémité du vibreur, exprimer y_S en fonction du temps.

La lame métallique d'un vibreur, fixée en un point O à une corde tendue, est animée d'un mouvement sinusoïdal de fréquence 100 Hz. Un ébranlement d'amplitude a=1,0 mm se propage le long de la corde avec une célérité de 40,0 cm/s. A l'autre extrémité de la corde, on a installé un dispositif anti-réflexion.

1. Calculer la période T et la longueur d'onde l de l'onde.
2. Ecrire l'équation horaire du mouvement du point O en prenant comme origine des temps le début de l'ébranlement, le déplacement se faisant dans le sens positif ascendant.
3. En déduire l'équation horaire du mouvement d'un point M situé à 3,30 cm de O.
4. Représenter l'aspect de la corde aux instants t₁=0,01 s et t=0,0125 s.

Un point O de la surface de l'eau est animé d'un mouvement sinusoïdal de fréquence 18 Hz d'amplitude 3,0 mm. Les ondes qui se propagent à la surface de l'eau ont une célérité de 2,7 m/s. A l'instant t=0, le mouvement de O commence dans le sens positif ascendant.

1. Donner l'équation horaire du mouvement de O.
2. Calculer la longueur d'onde l de l'onde.
3. Quelle est la différence de phase entre deux points A et B situés respectivement à 14,7 cm et 7,2 cm du point O ?

La houle est une onde caractérisée par sa période (intervalle de temps séparant le passage de deux crêtes successives devant un obstacle fixe) ; sa longueur d'onde (distance entre deux crêtes successives) , sa vitesse de propagation , sa hauteur (dimension entre la crête et le creux) et sa cambrure (rapport entre la hauteur et la longueur d'onde).

La houle est un système de vagues à faible cambrure se propageant en dehors du domaine, appelé fetch , où elle naît sous l'influence du vent.

1. schématiser l'onde.
2. Représenter l'amplitude et la hauteur de la houle.
3. L'amplitude de la houle est-elle égale à la hauteur des vagues ?
4. Ecrire la relation entre l'amplitude et la hauteur.
5. Quelle est la nature de cette onde ?
6. Une houle haute de 7 m a une période de 15 s et se propage à la vitesse de 85 km/h. Quelle est sa cambrure ? 

 

y_M(x,t)=0,04sin(2p/0,01 (t- x/2 ))

w= 2p/0,01 = 2p/T d'où T= 0,01 s et f=100 Hz.

M reproduit le mouvement de la source avec un retard t = x/ v = x/2 d'où célérité de l'onde : v=2 m/s

longueur d'onde l = v/f = 2 / 100 = 2 10^-2 m= 2 cm

ondes transversales d'amplitude 0,04 m = 4 cm.

y_S(x,t)=0,04sin(2p/0,01 t)

---

période T= 1/100 = 0,01 s ; longueur d'onde (m)= célérité (m/s) /fréquence (Hz) = 0,4 /100 = 4 10^-3 m.

y_O(x,t)=0,01sin(2p/0,01 t)

M reproduit le mouvement de la source avec un retard t = x/ v = 0,033/0,4 =8,25 10^-2 s.

y_M(x,t)=0,01sin(2p/0,01 (t- 0,0825))

---

y_O(x,t)=0,003sin(2p*18 t)=0,003sin(36p t)

longueur d'onde(m) =célérité (m/s) /fréquence (Hz) = 2,7 /18 = 0,15 m.

14,7-7,2 = 7,5 cm soit une demi-longueur d'onde.

en conséquence A et B, séparés par un nombre impair de demi-longueur d'onde sont en opposition de phase.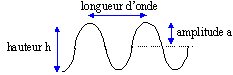

---

amplitude = ½ hauteur

onde progressive transversale.

vitesse en m/s : 85 / 3,6 = 23,61 m/s

longueur d'onde(m) =célérité (m/s) * période (s) = 23,61 *15 = 354 m.

cambrure = hauteur / longueur d'onde = 7 / 354 = 0,02

---

la tonalité du télephone

1. Le son émis par la tonalité du téléphone est quasi sinusoïdal. Sa fréquence est de 440 Hz , la fréquence identique à celle du son émis par un diaposon, le la3 . Calculer la période T de cette onde sonore.
2. La célérité du son dans l'air sec à 0°c et à la pression de 101325 Pa est de v = 331,45 m/s. Calculer la longueur d'onde de l'onde sonore émise par la tonalité du téléphone dans l'air considéré précédemment. Attention aux nombres de chiffres significatifs du résultat !
3. La célérité du son dans un gaz est proportionnelle à la racine carrée de la température absolue de l'air dans lequel se propage le son. On considère maintenant un air sec à la température de 27°C et à la pression de 101325 Pa
   - Calculer la célérité du son sans cet air.
   -Calculer la nouvelle longueur d'onde de l'onde émise par la tonalité du téléphone.

télémètre :

Un télémètre comporte, dans un même boîtier, un émetteur et un récepteur d'ondes ultrasonores de fréquence 40 KHz. Pour mesurer la distance d où se situe un obstacle on oriente l'appareil dans sa direction, puis on déclenche l'émission. Cette-ci est interrompue dès que le récepteur reçoit l'onde réfléchie.

La durée d'émission est déterminée par comptage et affichage du nombre d'impulsions délivrées par un oscillateur de fréquence f . L'affichage comporte 3 digits et clignote en cas de dépassement de la capacité de mesure. L'étalonnage de l'appareil est réalisé à 20 °C, pour une célérité de l'onde ultrasonore de 342 m/s. Une unité affichée correspond alors à une distance d de 1 cm.

1. Quelle distance maximale peut être mesurée par le télémètre ?
2. Quelle est, pour cette distance, la durée totale de propagation de l'onde ultrasonore ?
3. Quelle doit être la valeur de la fréquence f de l'oscillateur ?
4. La télémètre indique une distance d=850 cm pur une mesure effectuée alors que la température est égale à 10 °C. La distance réelle est-elle supérieure ou inférieure à cette valeur ?
5. Quelle est l'erreur commise sur cette mesure ?
6. On rappelle que la célérité des ultrasons est proportionnelle à la racine carrée de la température absolue.